[分治]浅谈快速排序

浅谈快速排序

什么是快速排序?

快排每次会选取一个排序基数,将这个序列分为一边是小于这个基数的,另一边是大于这个基数的.当然,你可以决定哪一边是大于或者小于的.
快速排序的期望时间复杂度为 \(O(nlogn)\) , 当然也与数据和所取的 排序基数 \(key\) 有关,对于一些数据,如果 \(key\) 的取值不当,快排就会退化成一个 \(O(n^{2})\) 的算法,这个后文会提到.

关于快速排序的操作

快速排序的基本思想是基于分治的一种排序.

对于一个序列,其下标为 \(l\) 至 \(r\) , \(l\) 的初始值为0, \(r\) 的初始值为 \(n-1\) .取一排序基数

注意, 这个排列基数是取一下标, 再将这个下标的值赋值给 \(key\)

\(key\), 然后进行快排操作.
这时候， 我们需要两个指针 \(i\) 和 \(j\). \(i\) 和 \(j\) 的初值分别为 \(l\) 和 \(r\).

然后只要 \(i\) 是小于等于 \(j\) 时, 我们就做着几件事

1. \(i\) 指针往后跳, 直到遇到 \(a[i]\) 的值是大于等于 \(key\) 的.
2. \(j\) 指针往前跳, 直到遇到 \(a[j]\) 的值是小于等于 \(key\) 的.
3. 若 \(i\) 是小于等于 \(j\) 的, 就交换 \(a[i]\) 和 \(a[j]\) 的值, \(i\) 再往后跳一位, \(j\) 再往前跳一位

图例说明1:

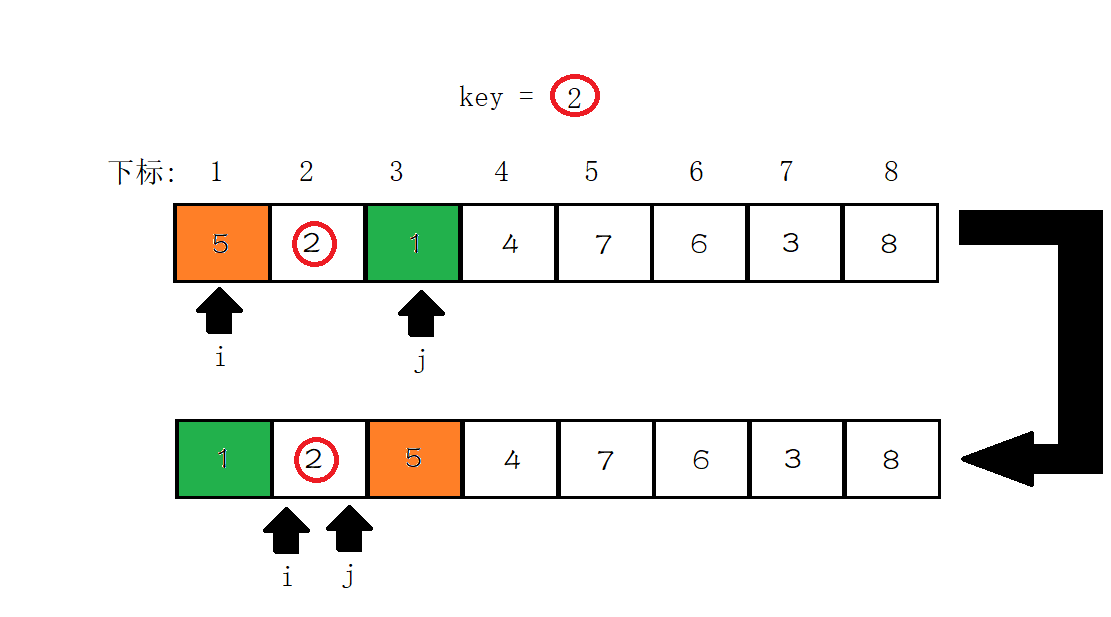
操作结束了之后, 我们不妨观察一下结果, 在随机抽取的的 \(key\) 的左侧(包括 \(key\) )都是大于等于 \(key\) 的, 右侧都是小于 \(key\) 的. 当然, 你可以通过修改判定, 已达到正序或者逆序的效果 (修改提到的前文的从 \(l,r\) 开始走的终点, 将终点的两个判定交换即可)

然后, 再进行递推, 再从 \(l\) 到 \(key\) 和 \(key + 1\) 到 \(r\) 进行 以上的操作, 当 \(l\) 小于 \(r\) 时这一次的递推就结束了.

图例说明2:

左边递推:

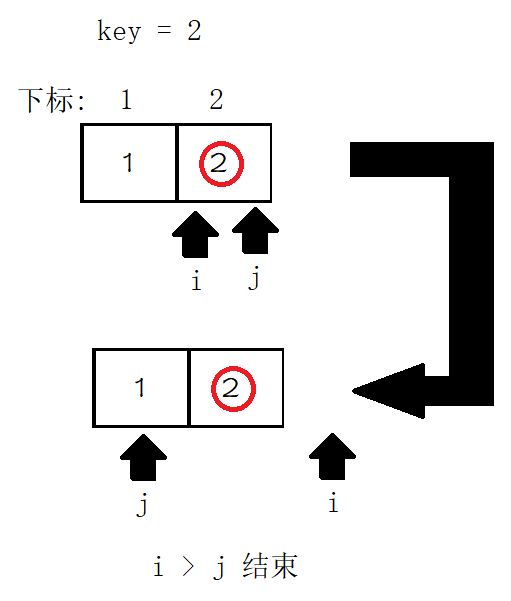
然后左边的剩下两个递归都只剩一个数, 直接 \(return\) 掉.

右边递推:

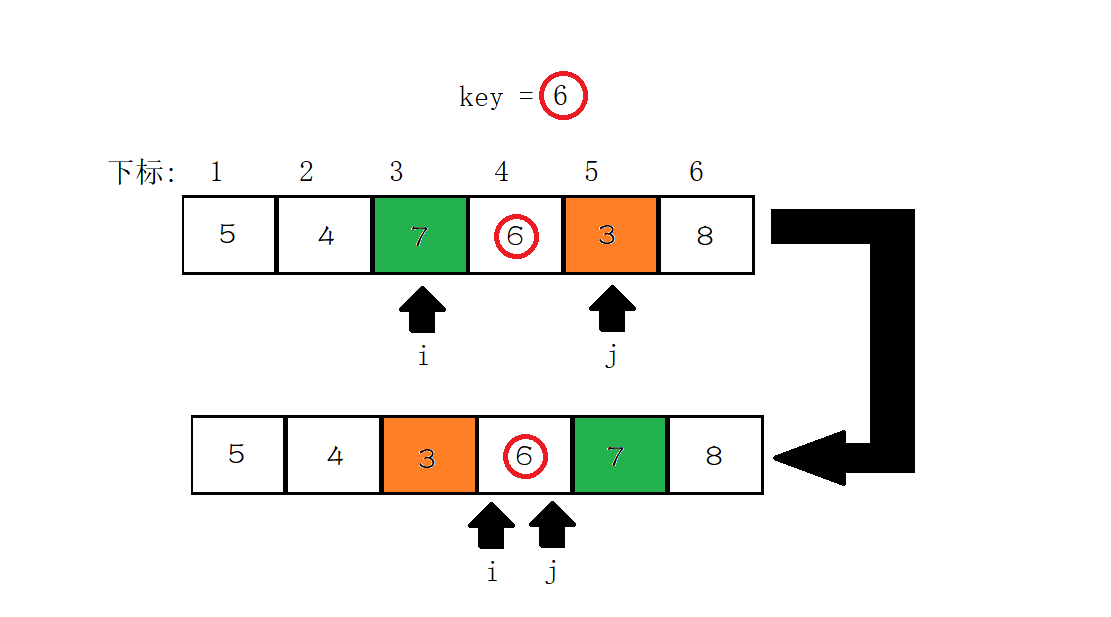
然后 \(i\) 和 \(j\) 相等了, 又可以继续递推.

读者可以通过模拟可发现， 出当 \(key\) 选为 \(a[0]\) 时, 对于一个已经排序好了的序列, 时间复杂度是会退化为 \(O(N^2)\) 的

Code

void sort_ (int l, int r) // a[]为输入的要排序的数列
{
	if (l >= r) return ;
	int i = l, j = r;
	int key = a[(l + r) / 2];
	do
	{
		while (a[i] < key) ++ i; // 可以修改成大于, 下面修改为小于以改变正逆序
		while (a[j] > key) -- j;
		if (i <= j)
		{
			swap (a[i], a[j]);
			++ i; -- j;	
		}  
		
	} while (i <= j);
	sort_ (l, j);
	sort_ (i, r);
}