[高精度]P1096 Hanoi 双塔问题
Hanoi 双塔问题
题目描述
给定A、B、C三根足够长的细柱,在A柱上放有2n个中间有孔的圆盘,共有n个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为n=3的情形)。
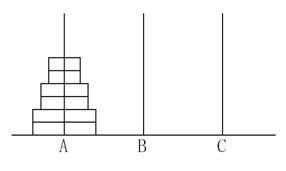
现要将这些圆盘移到C柱上,在移动过程中可放在B柱上暂存。要求:
(1)每次只能移动一个圆盘;
(2)A、B、C三根细柱上的圆盘都要保持上小下大的顺序;
任务:设An为2n个圆盘完成上述任务所需的最少移动次数,对于输入的n,输出An 。
输入格式
一个正整数n,表示在A柱上放有2n个圆盘。
输出格式
一个正整数, 为完成上述任务所需的最少移动次数An 。
输入输出样例
输入 #1
【输入样例1】
1
【输入样例2】
2
输出 #1
【输出样例1】
2
【输出样例2】
6
说明/提示
【限制】
对于50%的数据,1≤n≤25
对于100%的数据,1≤n≤200
题目解析
这个蒟蒻很懒,没有写题解
双塔和单塔不同的是:双塔的步数是单塔的2倍(肯定的)。
所以只要一个过程就行了。
我们看完题目,不难得出:总数量=2*n;
步数=(n-1块圆盘的步数)*2
可以用阶乘做。
AC完整程序
#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;
void input();
void add();
void mul();
void work();
void output();
const int maxx=1000;
int n,a[maxx];
int main(){
input();
work();
output();
return 0;
}
void input(){
scanf("%d",&n);
}
void work(){
memset(a,0,sizeof(a));
a[maxx-1]=2;
for(int i=2;i<=n;i++){
add();
mul();
}
}
void output(){
bool f=false;
for(int i=1;i<maxx;i++){
if(a[i]!=0){
if(!f)f=true;
printf("%d",a[i]);
}
else if(f)printf("%d",a[i]);
}
}
void add(){
a[maxx-1]++;
for(int i=maxx-1;i>0;i--){
a[i-1]+=a[i]/10;
a[i]%=10;
}
}
void mul(){
for(int i=maxx-1;i>0;i--){
a[i]*=2;
}
for(int i=maxx-1;i>0;i--){
a[i-1]+=a[i]/10;
a[i]%=10;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号