[GDKOI2021] 普及组 Day3 总结 && 题解

[ G D K O I 2021 ] 普 及 组 D a y 3 总 结

---

时间安排和昨天的GDKOI2021 Day2一样.

早上四个小时的快乐码题时间,然鹅我打了半小时的表😢
然后就是下午的题目讲解和凸包讲座.

---

题目讲解

---

T1

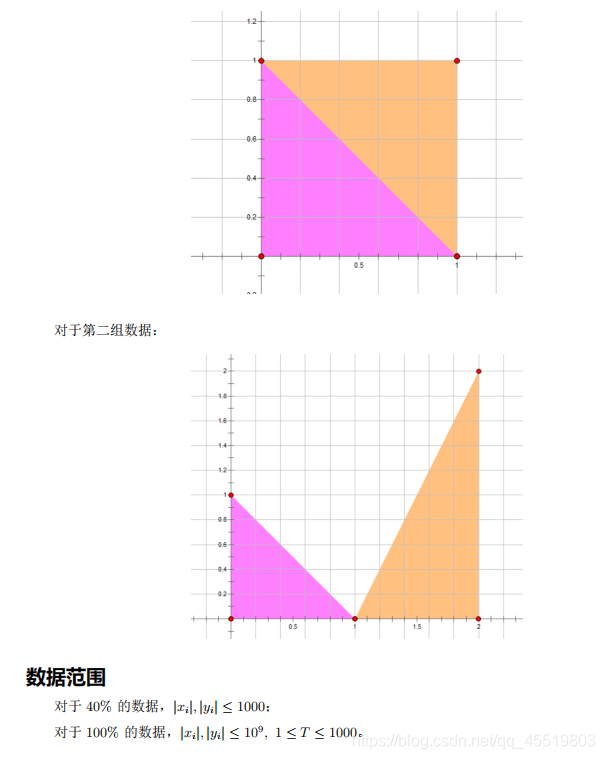
相似三角形的判定应该大家都知道,

一开始我还是用勾股来求的,结果打完后发现好像用欧氏距离简单的多…

关于我怎么用勾股来求边长的:

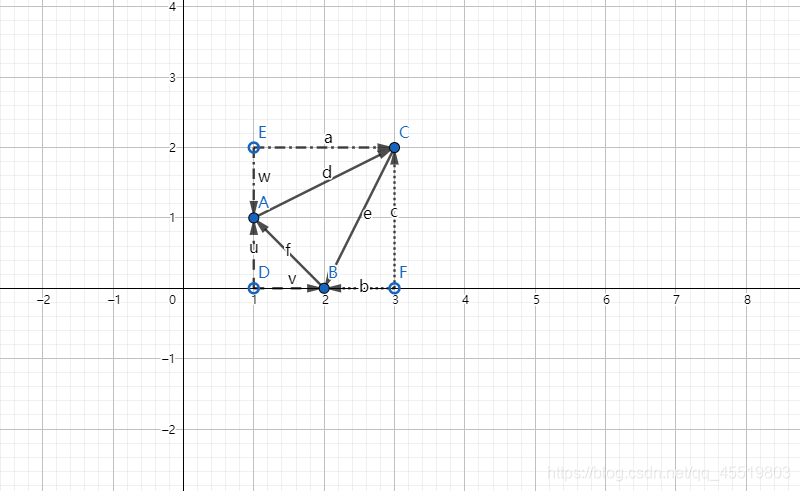
虚点是为了求边长而设定的辅助点,而实线是所求三角形的边.虚线是同辅助点建立的辅助边,由于是成$90°$的,所以可以用沟谷进行一个边的求长.因为知道了三角形三个点的位置,所以可以很容易地推导出符合这个要求的点,知道了辅助点和三角形的点的位置,又可以求出两条辅助边发的长度,然后就是勾股了.

---

T2

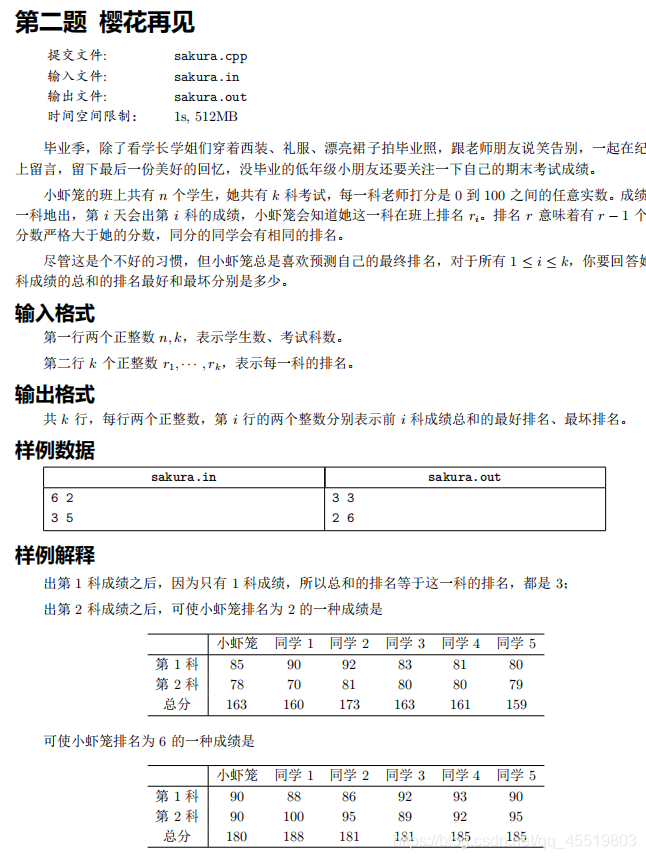
这题的思路很简单.由于成绩可能是任何实数,对于最优情况下就赋予99.99的成绩,比他高的($r-1$个)人就赋予 100分的成绩,比他低的就赋予$0$分的"好成绩".

对于最差的情况下,直接赋予最低的成绩, 0.如果没有人比他高,那么大家都是 0分,有比他高的都是$100$分,其他人都是$0$分.

---

T3

出现了,$Day1$讲过的数论
化简过程:

\begin{equation}
\sum_{k=1}^{n} \sum_{i \mid k} \sum_{j \mid i} \lambda(i) \lambda(j)=\sum_{k=1}^{n} \sum_{i \mid k} \lambda(i) \sum_{j \mid i} \lambda(j)
\end{equation}

我们设 

\begin{equation}
\operatorname{sum}(x)=\sum_{i \mid x} \lambda(i)
\end{equation}

如果我们通过枚举 i ，相当于贡献就是

\begin{equation}
\lambda(i) * \operatorname{sum}(i)
\end{equation}

，显然在 1~n 内的每一个$i$的倍数都有一次贡献。这样可以拿到 60分的部分分。

如果仔细分析

\begin{equation}
\operatorname{sum}(x)
\end{equation}

的值可以发现，
如果 x 为完全平方数，

\begin{equation}
\operatorname{sum}(x)=1
\end{equation}

，否则

\begin{equation}
\operatorname{sum}(x)=0
\end{equation}

证明:分解 x的质因数,使

\begin{equation}
x=p_{1}^{a 1} * p_{1}^{a 1}
\end{equation}

。
显然每个指数 i从0到 a;取值的积就是 x 的每一个因数。
假设存在一个 α_k是奇数，那么这个质数的指数可以选择 0 到 a_k ，奇数个数刚好等于偶数个数，说明每一种选择都恰好有一种选择与它的指数和奇偶性想法，即\operatorname{sum}(x)=0
如果 a_i​全为偶数，即为完全平方数，那么$1$。由前面的对称性可以知道，如果将某个质数的指数减小 2，$sum$值不变。所有完全平方数的$sum$值等于 \operatorname{sum}(x)=1。

然后继续化简公式
\sum_{k=1}^{n} \sum_{i \mid k} \lambda(i) * \operatorname{sum}(i)
因为只有$i$是完全平方数时， \operatorname{sum}(i)=1，而此时 \lambda(i)=1。那么答案就是每个完全平方数 x在 1 到 n 内的倍数的和。
即

\begin{equation}
\sum_{i^{2}<n} \frac{n}{i^{2}}
\end{equation}

---

T4

这道题有个很有意思的地方,就是序列前$i$个元素的和要大于后$n-i+1$个.这里由于$i$是最小等于$1$的,所以容易得出该要求的简化证明:该序列的第一个元素大于等于该序列其他元素之和才为题目定义的"好数列"
但如果就是不断地生成一个符合题目基本要求的序列,再去验证该序列是否为"好序列",那么通常会超出时限.于是我们就想到一个简化的思想

分析:
首先我们发现，如果某个长度为$i$的前缀与长度为$i$的后缀有重叠部分，那
么这个限制等价于长度为$n-i$的前缀。也就是说如果$n$是偶数，那么只需要
考虑前$n/2$位满足条件即可;如果$n$是奇数，也只需考虑$n/2$位即可，中间
那一位可以随便填。
考虑一个计数$DP$,以$f[i][j]$来表示对于前$i$位的和比后$i$位大$j$的方案数.
那么可以得出:
$$f[i][j]=\stackrel{j+n\sum }{k=max(j-n,0)}f[i][k]\ast (n+1-\left|j-k\right|)$$
时间复杂度为$O(n^4)$

---

讲座

凸包

---

个人感想

这次$GDKOI2021$真的是教给了我很多,不论是讲堂还是讲题部分,都是有很多值得学习了了解的知识点的知识面的.
同今天解压密码一样,$GDKOI$普及组,明年见