后缀表达式转换为中缀表达式

后缀表达式转换为中缀表达式

         之前我们介绍过《中缀表达式转化为后缀表达式》，现在我们想得到其逆过程，即如何由后缀表达式转换为中缀表达式。

         目前我先给出我的一种理解和实现，其他方法以后再议。

         有关中缀表达式的词法分析，本文不作考虑，而是直接用加了空格硬分割操作符和操作数的后缀表达式。

         我们先来回忆一下后缀表达式的计算方法，可参考《后缀表达式的计算》。后缀表达式的计算过程为：首先设置一个操作数栈，对后缀表达式进行从左到右的扫描，如果是操作数，则直接压栈，如果是操作符，则从操作数栈中弹出相应的操作数结合当前操作符进行相应的运算，后将运算而得的结果压入到栈中，直至扫描完整个栈后，如果该中缀表达式是合法的，则操作数栈中应该有且只有一个元素，该元素即为后缀表达式的结果。

         我们的方法是借鉴于后缀表达式计算的算法，基本算法逻辑都是一样的，不同的是，当我们扫描到操作符时，我们不做数值的运算，而是将相应的操作数和操作符进行拼接，并将拼接后的表达式压栈，直至扫描完成整个后缀表达式后，如果该后缀表达式是合法的，那么最后栈中应该只有一个元素，该元素即为后缀表达式对应的中缀表达式。这里的栈我们不能称之为操作数栈了，我们称其为表达式栈。

         另外，在我们的后缀表达式中，我们也是只局限于加减乘除四种运算。

         具体的程序如下：

// 后缀表达式转换为中缀表达式
#include <iostream>
#include <sstream>
#include <string>
#include <vector>
#include <stack>
#include <set>
using namespace std;

void get_postfix(vector<string>& postfix)
{
    postfix.clear();
    string line, op_op;
    getline(cin, line);
    istringstream sin(line);
    while (sin >> op_op)
    {
        postfix.push_back(op_op);
    }
}

void init_operators(set<string>& optors)
{
    optors.clear();
    optors.insert("+");
    optors.insert("-");
    optors.insert("*");
    optors.insert("/");
}

bool is_operator(const set<string>& optors, const string& str)
{
    auto cit = optors.find(str);
    if (cit != optors.end())
    {
        return true;
    }
    else
    {
        return false;
    }
}

void post_to_in(const vector<string>& postfix, string& infix, const set<string>& optors)
{
    infix.clear();
    if (postfix.empty())
    {
        return;
    }
    // 表达式栈
    stack<string> exp_stk;
    string a, b, c;
    for (auto i = 0; i != postfix.size(); ++i)
    {
        if (!is_operator(optors, postfix[i]))
        {
            exp_stk.push(postfix[i]);
        }
        else
        {
            switch (postfix[i][0])
            {
            case '+':
            case '-':
            case '*':
            case '/':
                b = exp_stk.top();
                exp_stk.pop();
                a = exp_stk.top();
                exp_stk.pop();
                c = "( " + a + " " + postfix[i] + " " + b + " )";
                exp_stk.push(c);
                break;

            default:
                break;
            }
        }
    }
    if (exp_stk.size() == 1)
    {
        infix = exp_stk.top();
    }
    else
    {
        infix = "后缀表达式非法，转换失败！";
    }
}

void display(const vector<string>& strs)
{
    for (auto cit = strs.begin(); cit != strs.end(); ++cit)
    {
        cout << *cit << ' ';
    }
    cout << endl;
}

int main()
{
    vector<string> postfix;
    string infix;

    set<string> optors;
    init_operators(optors);

    while (1)
    {
        get_postfix(postfix);

        post_to_in(postfix, infix, optors);

        display(postfix);
        cout << infix << endl;
        cout << endl;
    }

    return 0;
}

 

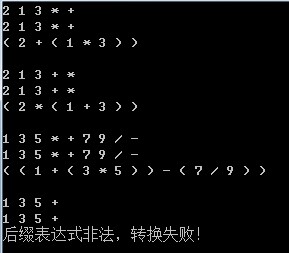
         从程序的运行结果我们可以看到，可以得到想要的结果。但是，每个单元子表达式都会加上了括号，有些括号并不是需要的。

         我们在后缀转中缀的过程中，并没有涉及加减乘除的优先级关系，针对每种运算符我们都是“加括号”处理。这种势必会造成产生多余的括号。

         下面我们尝试去除多余的括号。

         首先，我们举个例子：对于后缀表达式：

2 1 3 * +

         我们程序得到的结果为：

       ( 2 + ( 1 * 3 ) )

         而去除多余的括号后，其结果应该为：

       2 + 1 * 3

         对于后缀表达式：

       2 1 3 + *

         我们程序得到的结果为：

       ( 2 * ( 1 + 3 ) )

         而最简的形式应该为：

       2 * ( 1 + 3 )

         同样，对于后缀表达式：

后缀表达式	程序得到的结果	最简形式
1 3 * 2 +	( ( 1 * 3 ) + 2 )	1 * 3 + 2
1 3 + 2 *	( ( 1 + 3 ) * 2 )	( 1 + 3 ) * 2

 

         我们的程序处理的方式是，当遇到操作符时，默认都会加上括号，显然有些括号是不需要加的，关于括号有没有必要加，需要取决于后面的操作符。如果后面的操作符优先级大于当前操作符，则需要加上括号，如果小于或等于则不需要加括号。如果当前操作符是最后一个操作符，则也不需要添加括号。这就需要我们建立两个数据结构：

         1.记录操作符优先级的结构

         2.按照后缀表达式中操作符的顺序，记录后缀表达式中的所有操作符

         根据以上分析，我们改进后的程序为：

// 改进1
#include <iostream>
#include <sstream>
#include <string>
#include <vector>
#include <stack>
#include <map>
using namespace std;

void get_postfix(vector<string>& postfix)
{
    postfix.clear();
    string line, op_op;
    getline(cin, line);
    istringstream sin(line);
    while (sin >> op_op)
    {
        postfix.push_back(op_op);
    }
}

void init_operators(map<string, int>& optors)
{
    optors.clear();
    optors["+"] = 100;
    optors["-"] = 100;
    optors["*"] = 200;
    optors["/"] = 200;
}

bool is_operator(const map<string, int>& optors, const string& str)
{
    auto cit = optors.find(str);
    if (cit != optors.end())
    {
        return true;
    }
    else
    {
        return false;
    }
}

void post_to_in(const vector<string>& postfix, string& infix, map<string, int>& optors)
{
    infix.clear();
    if (postfix.empty())
    {
        return;
    }
    vector<string> post_optors; // 按照后缀表达式操作符的顺序，记录表达式中的操作符
    for (auto i = 0; i != postfix.size(); ++i)
    {
        if (is_operator(optors, postfix[i]))
        {
            post_optors.push_back(postfix[i]);
        }
    }
    auto pos = 0; // 记录当前操作符在post_optors中的位置

    // 表达式栈
    stack<string> exp_stk;
    string a, b, c;

    for (auto i = 0; i != postfix.size(); ++i)
    {
        if (!is_operator(optors, postfix[i]))
        {
            exp_stk.push(postfix[i]);
        }
        else
        {
            switch (postfix[i][0])
            {
            case '+':
            case '-':
            case '*':
            case '/':
                b = exp_stk.top();
                exp_stk.pop();
                a = exp_stk.top();
                exp_stk.pop();

                // 加括号 || 不加括号
                ++pos;
                if (pos < post_optors.size() && optors[post_optors[pos]] > optors[postfix[i]])
                {
                    c = "( " + a + " " + postfix[i] + " " + b + " )";
                }
                else
                {
                    c = a + " " + postfix[i] + " " + b;
                }
                
                exp_stk.push(c);
                break;

            default:
                break;
            }
        }
    }
    if (exp_stk.size() == 1)
    {
        infix = exp_stk.top();
    }
    else
    {
        infix = "后缀表达式非法，转换失败！";
    }
}

void display(const vector<string>& strs)
{
    for (auto cit = strs.begin(); cit != strs.end(); ++cit)
    {
        cout << *cit << ' ';
    }
    cout << endl;
}

int main()
{
    vector<string> postfix;
    string infix;

    map<string, int> optors;
    init_operators(optors);

    while (1)
    {
        get_postfix(postfix);

        post_to_in(postfix, infix, optors);

        display(postfix);
        cout << infix << endl;
        cout << endl;
    }

    return 0;
}

 

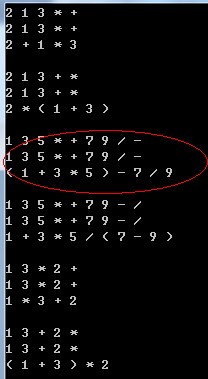
         从程序结果我们可以看出，程序基本符合预期，但是对于：

后缀表达式	程序得到的结果	最简形式
1 3 5 * + 7 9 / -	( 1 + 3 * 5 ) – 7 / 9	1 + 3 * 5 – 7 / 9

         原因在于，我们检测到+的优先级小于/的优先级，所以对 1 + 3 * 5 加了括号，但是 / 前面已经有了两个操作数：7和9，所以，对于 1 + 3 * 5 已没有必要添加括号，这就需要我们还要考虑相邻两个操作符在后缀表达式中的位置关系，不仅仅是前后的关系，还有他们之间的操作数的个数与他们是几目运算符的关系。

         这里，我们对数据结构：记录操作符在后缀表达式中的顺序，还要记录操作符对应于后缀表达式中的位置。

         具体的程序如下：

// 改进2
#include <iostream>
#include <sstream>
#include <string>
#include <vector>
#include <stack>
#include <map>
using namespace std;

void get_postfix(vector<string>& postfix)
{
    postfix.clear();
    string line, op_op;
    getline(cin, line);
    istringstream sin(line);
    while (sin >> op_op)
    {
        postfix.push_back(op_op);
    }
}

void init_operators(map<string, int>& optors)
{
    optors.clear();
    optors["+"] = 100;
    optors["-"] = 100;
    optors["*"] = 200;
    optors["/"] = 200;
}

bool is_operator(const map<string, int>& optors, const string& str)
{
    auto cit = optors.find(str);
    if (cit != optors.end())
    {
        return true;
    }
    else
    {
        return false;
    }
}

void post_to_in(const vector<string>& postfix, string& infix, map<string, int>& optors)
{
    infix.clear();
    if (postfix.empty())
    {
        return;
    }

    // 添加位置信息
    struct op_pos 
    {
        string op;    // 操作符
        int    pos;   // 在后缀表达式中的位置
        int    pol;   // 几目运算符
    };
    vector<op_pos> post_optors; // 按照后缀表达式操作符的顺序，记录表达式中的操作符
    op_pos tmp;
    for (auto i = 0; i != postfix.size(); ++i)
    {
        if (is_operator(optors, postfix[i]))
        {
            tmp.op = postfix[i];
            tmp.pos = i;
            tmp.pol = 2; // 可以在optors中添加几目信息，并在这里通过optors进行赋值
            post_optors.push_back(tmp);
        }
    }
    auto pos = 0; // 记录当前操作符在post_optors中的位置

    // 表达式栈
    stack<string> exp_stk;
    string a, b, c;

    for (auto i = 0; i != postfix.size(); ++i)
    {
        if (!is_operator(optors, postfix[i]))
        {
            exp_stk.push(postfix[i]);
        }
        else
        {
            switch (postfix[i][0])
            {
            case '+':
            case '-':
            case '*':
            case '/':
                b = exp_stk.top();
                exp_stk.pop();
                a = exp_stk.top();
                exp_stk.pop();

                // 加括号 || 不加括号
                ++pos;
                if (pos < post_optors.size() && optors[post_optors[pos].op] > optors[postfix[i]]
                 && post_optors[pos].pos - post_optors[pos - 1].pos < post_optors[pos].pol + 1 /* 这里需要加1，因为记录的是两个操作符的位置 */)
                {
                    c = "( " + a + " " + postfix[i] + " " + b + " )";
                }
                else
                {
                    c = a + " " + postfix[i] + " " + b;
                }
                
                exp_stk.push(c);
                break;

            default:
                break;
            }
        }
    }
    if (exp_stk.size() == 1)
    {
        infix = exp_stk.top();
    }
    else
    {
        infix = "后缀表达式非法，转换失败！";
    }
}

void display(const vector<string>& strs)
{
    for (auto cit = strs.begin(); cit != strs.end(); ++cit)
    {
        cout << *cit << ' ';
    }
    cout << endl;
}

int main()
{
    vector<string> postfix;
    string infix;

    map<string, int> optors;
    init_operators(optors);

    while (1)
    {
        get_postfix(postfix);

        post_to_in(postfix, infix, optors);

        display(postfix);
        cout << infix << endl;
        cout << endl;
    }

    return 0;
}

 

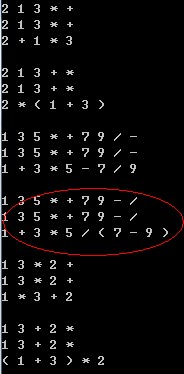
         上述程序针对1 3 5 * + 7 9 / - 这种情况可以得到我们想要的结果，但是对于 1 3 5 * + 7 9 - / 这种情况还是不能很好的解决（第二个程序这种情况也是无法解决）。

         所以，我们还需要改进我们的程序，在顺序扫描后缀表达式过程中，我们记录每个操作符负责的操作数的个数。比如针对 1 3 5 * + 7 9 - /，我们顺序扫描时，当扫描到*时，这时已经经历了3个操作数，到*操作符时，需要扣除2个操作数，生成一个操作数，所以当扫描到+时，这时+对应的操作数个数为2个，当到-时，-对应的操作数个数为4，-会将前面两个操作数变为1个，所以/需要波及到前面的表达式，这种情况需要加括号处理。这种情况，+和/之间间隔了-，不能仅仅依靠后缀表达式中两个相邻的操作符来判断是否添加括号。这里我们不再继续。

         如果能够针对前缀、中缀、后缀表达式都能简历相应的二叉树，那么就可以利用二叉树的前序、中序、后序得到对应的前缀、中缀、后缀表达式，另外有关表达的计算也会迎刃而解。

         后续，关于前缀、中缀、后缀表达式之间的相互转换，我们主要有以下几个方面需要探讨：

         1.以上3个程序是我根据后缀表达式的计算进行的摸索，客观上说，只有第一个程序是完全正确的，后面两个改进为了得到最简的形式，但是存在一些错误，主要集中在如何添加括号方面。下一步，我们将在网上寻求更为好的后缀表达式转换为中缀表达式的算法。

         2.中缀到后缀、后缀到中缀、中缀到前缀、前缀到中缀、后缀到前缀、前缀到后缀，这六种转换有待我们逐个解决。

         3.中缀到后缀的转换，我们先设置一个操作符栈，然后进行的相关操作，就像前面提到的，我们能否根据前轴、中缀、后缀中的任意一种表达式建立一个树，然后对树进行相应的前序、中序、后序的操作。对表达式建立相应的语法树是解决六种转换的根本方法。