HDU 1198 Farm Irrigation(状态压缩+DFS)

题目网址:http://acm.hdu.edu.cn/showproblem.php?pid=1198

题目：

Farm Irrigation

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10132    Accepted Submission(s): 4464

Problem Description

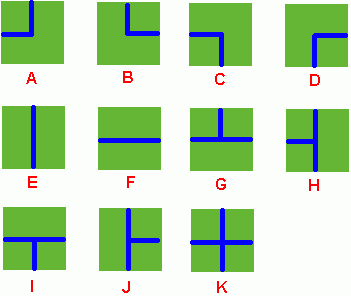
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 

ADC
FJK
IHE

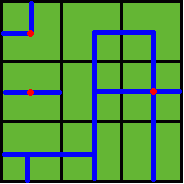
then the water pipes are distributed like 


Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? 

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2

DK

HF

3 3

ADC

FJK

IHE

-1 -1

 

Sample Output

2

3

 

思路：

这道题很明显就是叫我们求连通块的数量。求连通块无非就是并查集和DFS两种方法，个人认为并查集更适合题目给定两两关系的情况，所以该题我用了DFS。而这道题又和传统的DFS有所不同，涉及到水管的拼接问题。因为四个方向拼接，我们很容易想到用状态压缩来解决。下面我简单地介绍一下状态压缩。

以A为例：

至于我为什么要将二进制状态排成“上左右下”而不是“左右上下”之类的呢。因为水管接通不止要考虑本身，还有下一个管道的方位，两个管道的方位都是相反的。比如J,K，J提供右管道，K提供左管道才能拼接成功。我们设d为J要提供的管道方位，则K提供的管道方位 我们就可以用3-d得出了，这样说有点抽象，看下面的代码会更好理解。

 

代码：

#include <cstdio>
#include <cstring>
char farm[55][55];
int mp[15]={12,10,5,3,9,6,14,13,7,11,15};//将A-K状态压缩
int visited[55][55];
int dirx[4]={1,0,0,-1};
int diry[4]={0,1,-1,0};
int n,m;
void dfs(int i,int j){
    int x=farm[i][j]-'A';
    int vx=mp[x];
    for (int d=0,xx,yy; d<4; d++) {
        xx=i+dirx[d];
        yy=j+diry[d];
        if(xx<0 || xx>=n || yy<0 || yy>=m ||visited[xx][yy])    continue;
        int t=farm[xx][yy]-'A';
        int vt=mp[t];
        if((vx>>d)&1 && (vt>>(3-d))&1){//连接水管的方向相反
            visited[xx][yy]=1;
            dfs(xx, yy);
        }
    }
}
int main(){
    int res;
    while (scanf("%d%d ",&n,&m)!=EOF && n!=-1 && m!=-1) {
        res=0;
        memset(visited, 0, sizeof(visited));
        for (int i=0; i<n; i++) gets(farm[i]);
        for (int i=0; i<n; i++) {
            for (int j=0; j<m; j++) {
                if(visited[i][j])   continue;//visited[i][j]不等于0，则说明它已经属于别的连通块了
                visited[i][j]=1;
                res++;
                dfs(i,j);
            }
        }
        printf("%d\n",res);
    }
    return 0;
}