Problem P34. [算法课分支限界法]硬币问题
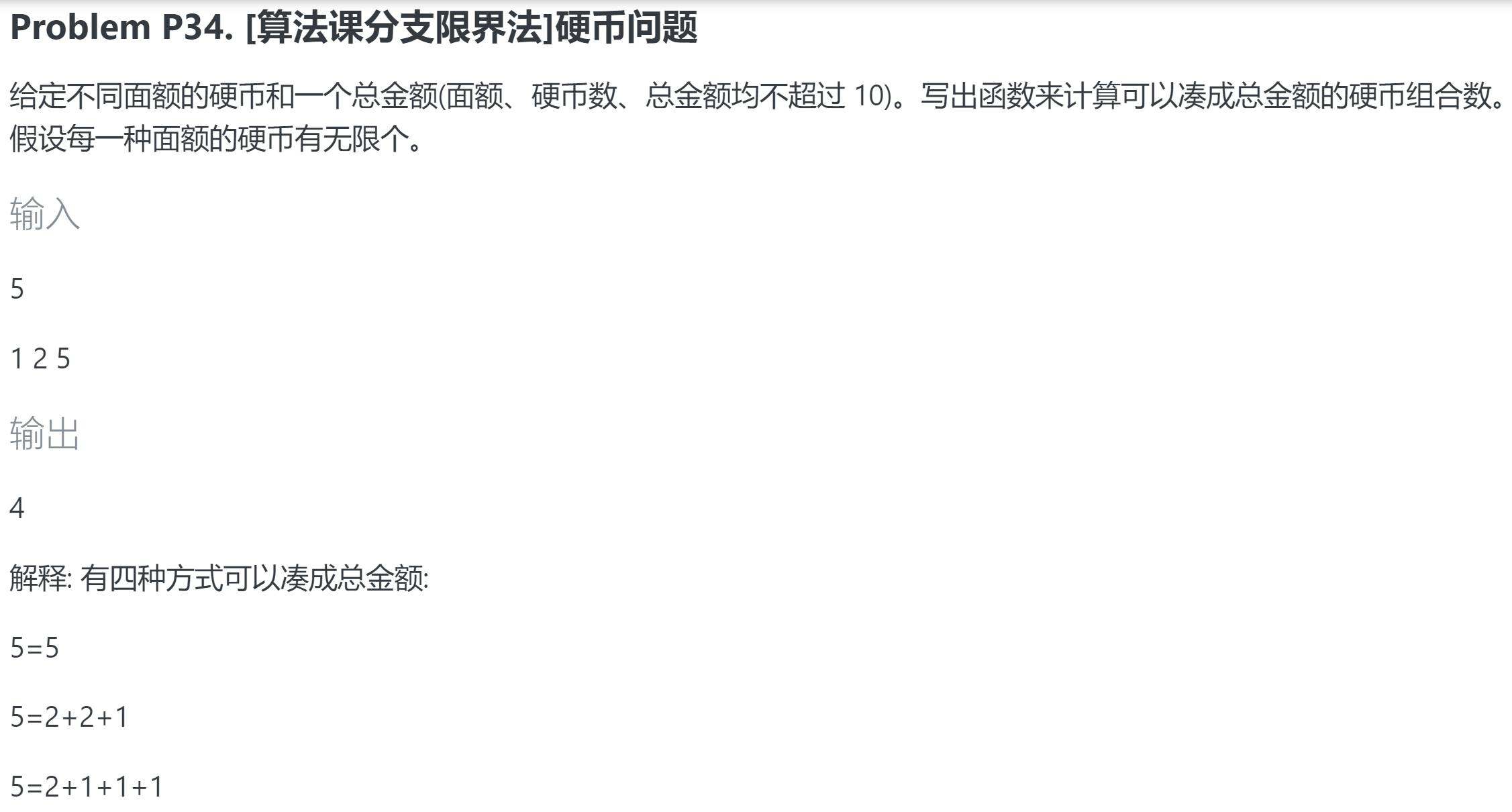
根据题目可以联想到无限个数物品的背包问题,
dp[j]表示能组合为 j 的个数是多少,外层 i 循环是遍历表示加入第 i 个数之后的状态,因为是无限个数,所以内层循环是正序遍历,加了一次第 i 个数之后,可以在它基础上继续加第 i 个数。
该题有两个要注意的地方:
- 因为算的是组合个数,所以
dp[j+num]+=dp[j];,已有 j 的 dp[j] 个组合,在此之上加上 num ,那么 dp[j] 个组合的情况下都可以加上 num。vector.size()是得到一个无符号整数,需要像将其转化为有符号整数,int n = dp.size();,要不然输入比如 2 5 的情况下就会出错。因为无符号数减去有符号数自动转化为前面的无符号数类型。
#include<iostream>
#include<bits/stdc++.h>
#include<cstdio>
#include<string>
using namespace std;
int main()
{
vector<int> nums;
while (1) {
int d;
int ret = scanf("%d", &d);
if (ret == EOF) {
break;
}
nums.push_back(d);
}
int sum = nums[0];
auto it = nums.begin();
nums.erase(it);
vector<int> dp = vector<int>(sum+1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
int num = nums[i];
int n = dp.size();
for (int j = 0; j < n-num; j++) {
if (dp[j] > 0) {
dp[j+num]+=dp[j];
}
}
}
cout << dp[sum] << endl;
return 0;
}


