【算法1-1】高精度

　其实我不是很擅长写文章的，但是呢，凡是都要有尝试的嘛，关于最近蓝桥杯的算法总结推送，我可能会选择其中的7到8个经典算法来写一下。

    那么首先第一个有请的嘉宾是高精度先生，高精度先生，请问你是怎么冒出来的呢？ 因为在数字运算时，long long都装不下结果了，所以只好由我顶上来了。long long在C++中大概支持十进制下大约19位数，而当运算的数字超过19位数的时候就要用到用一个数组来表示一个数字，并进行模拟加减乘除等运算，这就是高精度算法。

    到底怎么做呢？我这里就用最简单的高精度加法来引出大家的思路。

    一天张三想做9位数的加法运算，他怕溢出，所以他用了long long。又一天，李四想做19位的加法运算，他也怕溢出，所以他用了数组。李四想我这19个数，每个位上的数当成int类型的数组s一个一个元素，如190，那么s[0] = 0， s[1] = 9, s[2] = 1。这时候就有人问了为啥是倒过来存的，不是s[0] = 1， s[2] = 0？这里存在一个问题，如果是正着存放，那么190+902 = 1092，这个1的存储就得把1后面的兄弟都往后挪一位，就会更加麻烦。

    回到刚刚讲到的进位问题，那么190 + 902， 就是s[0]+2, s[1]+0，s[2]+1, 这时候s[2]就为10了，众所周知，个位数上只有0~9，没有10，所以要做进位处理，s[3] = 1, s[2] = 0 ,这样s[3]s[2]放在一起看就是10了。但是呢，其实前面的演示不太正确，因为一般并不是两个大数进行相加，而是一般是由一个大的数加很多小的数，一直加在大的数上，所以这样就只用用到一个数组来存储大数就行了！

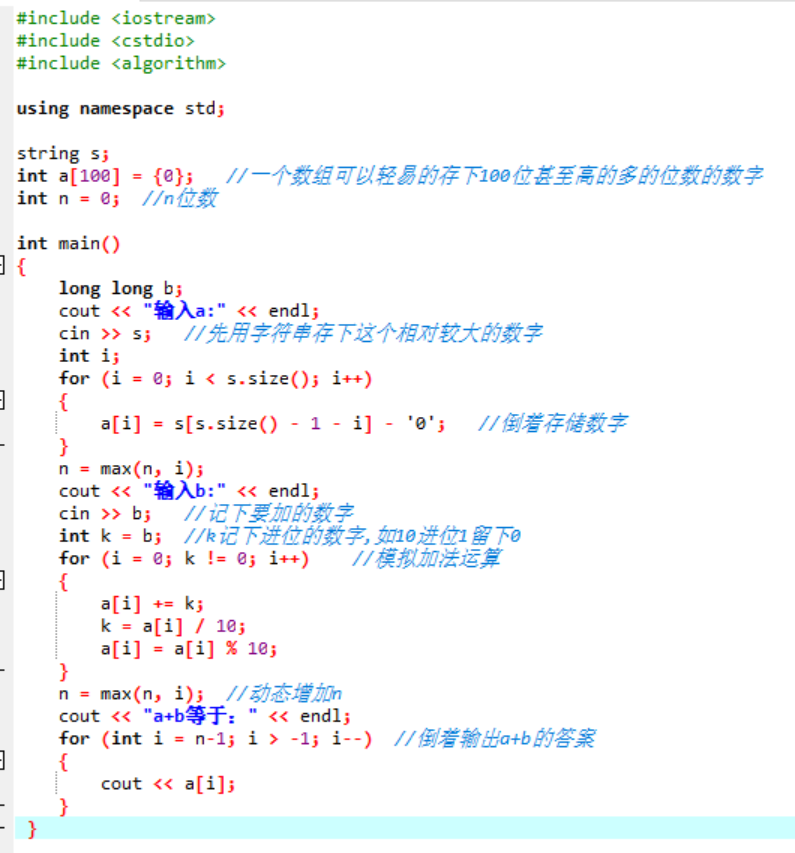
    看懂了中文，接下来咱们看一下代码，接下来是高精度加法的代码演示：