一文教你快速搞懂速度曲线规划之T形曲线（超详细+图文+推导+附件代码）

 

运动控制中常用的T速度曲线规划的原理和程序实现，最后给出了测试结果；
如果本文帮到了您，请帮忙点个赞 👍👍👍；
如果本文帮到了您，请帮忙点个赞 👍👍👍；
如果本文帮到了您，请帮忙点个赞 👍👍👍；

 

文章目录

• 1 前言
• 2 理论分析
• 3 matlab 实现
• 4 测试结果
• 5 c语言实现
• 6 总结

 

1 前言

在伺服系统以及控制系统的加减速动作中，为了让速度更加平滑，可以引入T型速度曲线规划（T-curve velocity profile），T曲线是工业界广泛采用的形式，它是一种时间最优的曲线。一般情况，曲线加速和减速的过程是对称的，设给定速度上限为$v^{max}$。加速度上限为$a^{max}$，被控对象从A点运动到B点，要求生成的轨迹在这些条件下时间最优¹。

2 理论分析

在整体系统高速启动，制动的状态下，可以提高整体系统的性能。每当系统完成一个动作的时候，总共包括三个过程，匀加速，匀速，匀减速，具体如下图所示；

根据$v$是否到达$v^{max}$，这里通常要分为两种情况来讨论；

• 第一种：速度到达$v^{max}$，最终速度曲线为梯形；
• 第二种：速度没有到达$v^{max}$，最终速度曲线为三角形；

下面仅讨论第一种情况；

这里时间使用$t$加脚标来表示，位置量使用$p$来表示，加速度使用$a$来表示

• 设加速时间长度为$t^a$：$t^0—t^1$；
• 因为加速和减速的过程是对称的，所以减速带的时间长度也为$t^a$：$t^2—t^3$；
• 最大速度$v^{max}$c持续的时间长度为$t^m$：$t^1—t^2$；

在实际的系统中，梯形曲线通常需要设置三个参数：

1. 最大速度$v^{max}$；
2. 加速度$a^{max}$；
3. 最终位置值$P^{final}$，下面简称为$P^f$；

所以这三个参数可以作为已知量来处理；

下面简单推到这三个参数之间的关系：
设加减速区域经过的位置量为$P^a$,则：
$$P^a=\genfrac{}{}{0ex}{}{1}{2}{a}^m{t}^a$$

设最大区域经过的位置量为$P^m$,则：
$$\{\begin{array}{l}{P}^m=v^m{t}^m\cdots ①\\ P^f=P^a+P^m+P^a\cdots ②\\ t^a=\genfrac{}{}{0ex}{}{v^{max}}{a^{max}}\cdots ③\\ t^m=\genfrac{}{}{0ex}{}{(P^f-2P^a)}{v^{max}}\cdots ④\end{array}$$
所以输出的位置量满足以下关系：
$$P(t)=\{\begin{array}{l}\genfrac{}{}{0ex}{}{1}{2}{a}^m{t}^2，t^0\le t\le t^1\\ \genfrac{}{}{0ex}{}{1}{2}{a}^m{t}^a+v^m(t-t^a),t^1<t\le t^2\\ \genfrac{}{}{0ex}{}{1}{2}{a}^m{t}^a+v^m{t}^m+\genfrac{}{}{0ex}{}{1}{2}{a}^m(t-t^m-t^a{)}^2,t^2<t\le t^3\end{array}$$
最终可以通过$P(t)$的关系以及①②③④式编写程序得到T型速度曲线规划。

3 matlab 实现

matlab的算法实现如下；

%% 梯形速度曲线
%% https://blog.csdn.net/u010632165
% Vm  最大熟读
% Am  最大加速度
% P   位置信号
%%
function t_curve(Vm,Am,P)

%设置初始条件
t0=0;
P0=0;       
Pf=P;       %最终位置
v_max=Vm;   %最大速度
a_max=Am;   %最大加速度

ta=v_max/a_max;     %加速和减速需要的时间
Pa=0.5*a_max*ta^2;  %加速或减速产生的位置量 
t_m=(Pf-2*Pa)/v_max;%最大速度需要的时间
t_f=t_m+2*ta;       %到达目标位置所需要的时间

t=t0:0.1:t_f;
n=size(t);
Pt=zeros(n(2),1);

i=1;
% 判断速度曲线规划属于哪一种情况
if t_f-2*ta>0  
    %达到最大速度，梯形
     for t=t0:0.1:t_f
         if t<=ta
             Pt(i)=P0+0.5*a_max*t*t;
         elseif ta<t && t<=t_f-ta
             Pt(i)=P0+0.5*a_max*ta*ta+a_max*ta*(t-ta);
         else 
             Pt(i)=Pf-0.5*a_max*(t_f-t)^2;
         end
         i=i+1;
     end
else 
    % 未达到最大速度，速度曲线为三角形
    ta=sqrt( (Pf-P0)/a_max);
    t_f=2*ta;
         for t=t0:0.1:t_f
             if t<=ta
                 Pt(i)=P0+0.5*a_max*t*t;
             else 
                 Pt(i)=Pf-0.5*a_max*(t_f-t)^2;
             end
             i=i+1;
        end
    
end
     subplot(3,1,1);
     plot(Pt);
     legend('位置曲线')
     subplot(3,1,2);
     plot(diff(Pt))
     legend('速度曲线')
     subplot(3,1,3);
     plot(diff(diff(Pt)))
     legend('加速度曲线')
end

4 测试结果

在matlab的命令终端输入以下指令；

 t_curve(3,1,20)

设置最大速度为3，加速度为1，最终位置为20；
仿真曲线如下所示；

5 c语言实现

在simulink中调用了c程序进行仿真测试，《一文教你快速学会在matlab的simulink中调用C语言进行仿真 》具体代码如下所示；

void sfun_myc_Outputs_wrapper(const real_T *u0,
			const real_T *u1,
			const real_T *u2,
			const real_T *t,
			real_T *y0,
			real_T *y1,
			real_T *y2)
{
/* %%%-SFUNWIZ_wrapper_Outputs_Changes_BEGIN --- EDIT HERE TO _END */
/* This sample sets the output equal to the input
      y0[0] = u0[0]; 
 For complex signals use: y0[0].re = u0[0].re; 
      y0[0].im = u0[0].im;
      y1[0].re = u1[0].re;
      y1[0].im = u1[0].im;
*/
/* %%%-SFUNWIZ_wrapper_Outputs_Changes_END --- EDIT HERE TO _BEGIN */
    int Am = u0[0];
    int Vm = u1[0];
    int Pf = u2[0];
    int T = t[0];
    
    int Ta = Vm/Am;
    int Tm = (Pf - Am*Ta*Ta)/Vm;
    int Tf = 2*Ta+Tm;
    printf("%d\r\n",Tf);    
    //梯形
    if(Tm>0){
        if(T <= Ta){
            y0[0] = 0.5*Am*T*T;
            y1[0] = Am*T;
            y2[0] = Am;
        }else if(T<=(Ta+Tm)){
            y0[0] = 0.5*Am*Ta*Ta + Vm*(T-Ta);
            y1[0] = Vm;
            y2[0] = 0;
        }else if(T<=(Ta+Tm+Ta)){
            y0[0] = 0.5*Am*Ta*Ta + Vm*Tm + 0.5*Am*(T-Ta-Tm)*(T-Ta-Tm);
            y1[0] = Vm-Am*(T-Ta-Tm);
            y2[0] = -Am;
        }
    }else{
    //三角形
        Ta = sqrt(Pf/Am);
        if(T<Ta){
            y0[0] = 0.5*Am*T*T;
            y1[0] = Am*T;
            y2[0] = Am;
        }else{
            y0[0] = 0.5*Am*Ta*Ta + 0.5*Am*(T-Ta)*(T-Ta);
            y1[0] = Am*Ta - Am*(T-Ta);
            y2[0] = -Am;
        }
    }
}

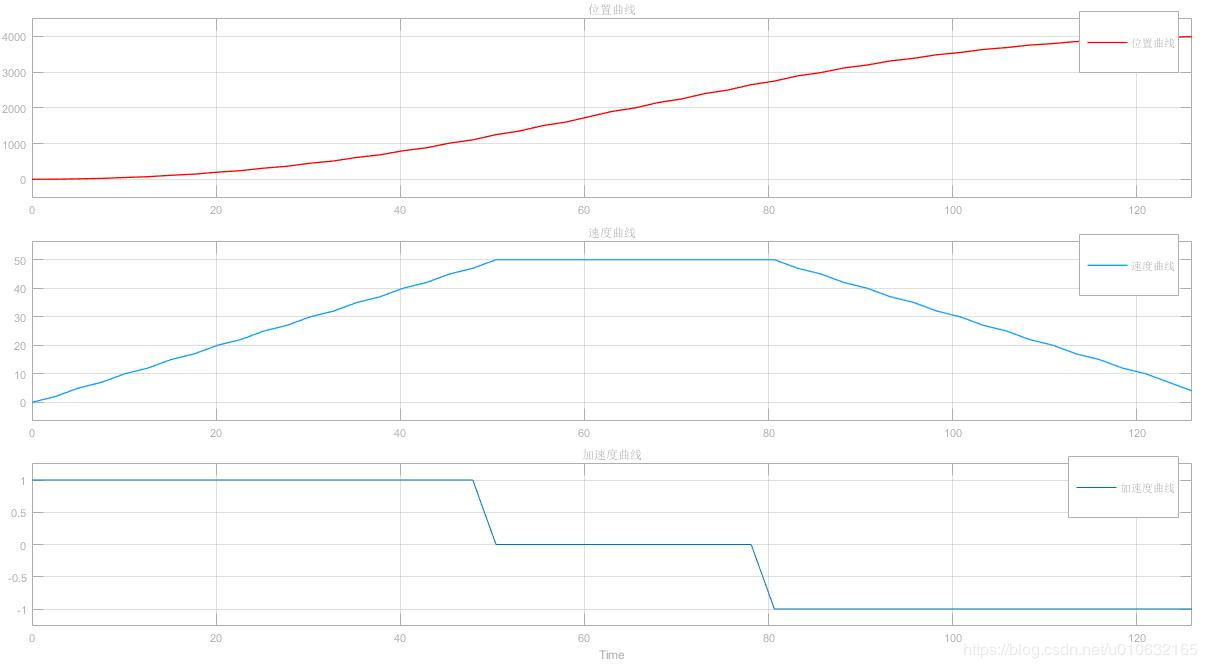
仿真结果如下；

6 总结

T曲线是工业界广泛采用的形式，在运动控制上，相比较S曲线，它算法的复杂度更低，所占用的系统资源更少，但是在恒加速的拐点会出现过冲，这里S曲线就可以减少这种情况的发生。本文写的相对比较简单，笔者能力有限，难免出现错误和纰漏，希望大佬不吝赐教。

文中难免有错误和纰漏之处，请大佬们不吝赐教
创作不易，如果本文帮到了您；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；

---

1. 《S/T曲线速度规划在定点DSP上的实现》 ↩︎