一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）

 

本文介绍了运动控制终的S曲线，通过matlab和C语言实现并进行仿真；本文篇幅较长，请自备茶水；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；

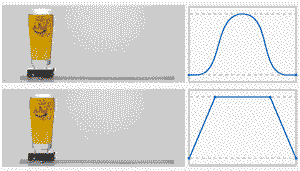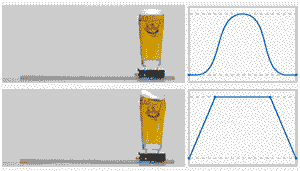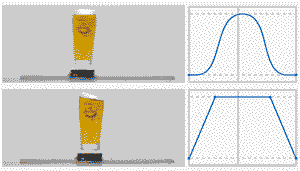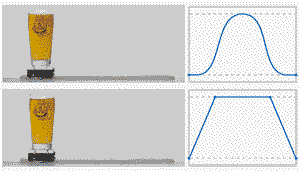
之前有介绍过T形曲线，具体可以参考《一文教你快速搞懂速度曲线规划之T形曲线》，本文将在原先的基础上进行进一步扩展，另外由于介绍速度曲线的论文较多，本文会在具体引用的地方给出原文出处；先对比一下两者的差别；

网图侵删

文章目录

• 1 前言
• 2 理论分析
• 2.1 加速度时间关系方程
• 2.2 速度时间关系方程
• 2.3 位移时间关系方程
• 3 程序实现的思路
• 3.1 $T^k$ 推导
• 3.2 $J$ 的推导
• 4 matlab 程序
• 5 总结
• 6 参考

 

1 前言

S形加减速的最重要特征是该算法的加速度/减速度曲线的形状如字母 S。S形加减速的速度曲线平滑 ,从而能够减少对控制过程中的冲击，并使插补过程具有柔性 ¹。
由于T形曲线在加速到匀速的切换过程中，实际中存在较大过冲，因此这里对比一下T曲线和7段S曲线的实际过程；

• T形：加速 -> 匀速 -> 减速
• S形：加加速($T^1$) -> 匀加速($T^2$) -> 减加速($T^3$)-> 匀速($T^4$)-> 加减速($T^5$)-> 匀减速($T^6$)-> 减减速($T^7$)

上文在加速这块的文字描述可能读起来起来有点绕，下面看图：

2 理论分析

由于S曲线在加减速的过程中，其加速度是变化的，因此这里引入了新的一个变量 $J$，即加加速度。
$$J=\genfrac{}{}{0ex}{}{d^a}{d^t}$$
因此对应上图的7段S速度曲线中，规定最大加速为$a^{max}$，最小加速度为$-a^{max}$，则加速度的关系；

• 加加速($T^1$)：$a$逐渐增大，此时$a=J{T}^1,0<t\le t^1;$
• 匀加速($T^2$)：$a$达到最大，此时$a=a^{max},t^1<t\le t^2;$
• 减加速($T^3$)：$a$逐渐减小，此时$a=a^{max}-J{T}^3,t^2<t\le t^3;$
• 匀速($T^4$)：$a$不变化，此时$a=0,t^3<t\le t^4;$
• 加减速($T^5$)：$|a|$ 逐渐减小，此时$a=-J{T}^5,t^4<t\le t^5;$
• 匀减速($T^6$)：$|a|$ 达到最小，此时$a=-a^{max},t^5<t\le t^6;$
• 减减速($T^7$)：$|a|$ 达到最小，此时$a=-a^{max}+-J{T}^7,t^6<t\le t^7;$

其中 $T^k=t^k-t^{k-1}(k=1,...,7)$

所以通常需要确定三个最基本的系统参数 :系统最大速度 $v^{max}$ ，最大加速度a_{max} ，加加速度$J$，就可以可确定整个运行过程² ；

• 最大速度：反映了系统的最大运行能力 ；
• 最大加速度：反映了系统的最大加减速能力 ；
• 加加速度：反映了系统的柔性；
  • 柔性越小，过冲越大，运行时间越短；
  • 柔性越大，过冲越小，运行时间越长；

2.1 加速度时间关系方程

整个加速度变化的过程具体如下图所示；


再次强调一下 $T$ 和 $t$ 的关系，$T^k=t^k-t^{k-1}(k=1,...,7)$
另外这里再引入变量 $\tau$，
$${\tau }^k=t-t^{k-1}\cdots ①$$
比如，当前时刻 $t^2<t\le t^3$ ,即 $t$ 位于区间 $T^3$，则如果将 $t^2$ 作为初始点，则 ${\tau }^3$w为 $t$ 相对于$t^2$时刻的时间，则有：
$${\tau }^3=t-t^2$$
下面可以得到加速度与时间的关系函数，具体如下：
$$\begin{array}{r}a(t)=\{\begin{array}{ll}Jt,& 0<t\le t^1\\ a^{max},& t^1<t\le t^2\\ a^{max}-J(t-t^2),& t^2<t\le t^3\\ 0,& t^3<t\le t^4\\ -J(t-t^4),& t^4<t\le t^5\\ -a^{max},& t^5<t\le t^6\\ -a^{max}-J(t-t^7),& t^6<t\le t^7\end{array}\end{array}\cdots ②$$

根据 ① 式，将 $\tau$ 代入 ② 式可以得到：
$$\begin{array}{r}a(t)=\{\begin{array}{ll}J{\tau }^1,& 0<t\le t^1\\ a^{max},& t^1<t\le t^2\\ a^{max}-J{\tau }^3,& t^2<t\le t^3\\ 0,& t^3<t\le t^4\\ -J{\tau }^3,& t^4<t\le t^5\\ -a^{max},& t^5<t\le t^6\\ -a^{max}+J{\tau }^7,& t^6<t\le t^7\end{array}\end{array}$$

上式中 $J>0$；

2.2 速度时间关系方程

速度和加速度满足 $v=at$ ；加加速度和速度的关系满足：
$$v=\genfrac{}{}{0ex}{}{1}{2}J{t}^2$$

结合加速度时间关系并结合② 式可以得到速度曲线关系，具体关系如下图所示；





进一步简化可以得到：

2.3 位移时间关系方程

位移 $S$ 和加加速度 $J$ 直接满足关系如下：
$$S=\genfrac{}{}{0ex}{}{1}{6}J{t}^3$$

简单推导
$$\{\begin{array}{l}S={\int }^{0}vdt\\ v=\genfrac{}{}{0ex}{}{1}{2}J{t}^2\end{array}$$
因此可以得到：
$$S={\int }^0\genfrac{}{}{0ex}{}{1}{2}J{t}^{2}dt=\genfrac{}{}{0ex}{}{1}{6}J{t}^3{|}^0$$

积分忘的差不多了，回去再复习一下；

最终位移的方程如下所示；

3 程序实现的思路

正如前面所提到的，S曲线规划需要确定三个最基本的系统参数 ：系统最大速度 $v^{max}$ ，最大加速度a_{max} ，加加速度$J$，这样就可以确定这个运行过程。
这里有一个隐性的条件，就是在运行的过程中可以达到最大速度，这样才是完整的7段S曲线，另外这里还有一些中间参数：

• $t^m=\genfrac{}{}{0ex}{}{v^{max}}{a^{max}}$，因此有 $T^1=T^3=T^5=T^7$；
• 加加速度 $J=J^1=J^3=J^5=J^7=\genfrac{}{}{0ex}{}{a^{max}}{t^m}$；
• $T^2=T^6$；
• $T^f$，用户给定整个运行过程所需要的时间；

但是通常实际过程中关心$a^{max}$，$v^{max}$，$T^f$；

3.1 $T^k$ 推导

理想状态假设存在 $T^2$和$T^6$，则推导过程如下：

$$\{\begin{array}{l}{v}^1=\genfrac{}{}{0ex}{}{1}{2}J{T}^1\\ v^2=v^1+a^{max}{T}^2\\ v^3=v^2+\genfrac{}{}{0ex}{}{1}{2}J{T}^3\\ v^3=v^{max}\\ T^1=T^3\end{array}$$

因此可以得到：
$$v^{max}=\genfrac{}{}{0ex}{}{1}{2}J{T}^1+a^{max}{T}^2+\genfrac{}{}{0ex}{}{1}{2}J{T}^1$$

简化之后得到：
$$v^{max}=J{T}^1+a^{max}{T}^2$$

根据②式可知：$a^{max}=J{T}^1$

最终得到：
$$T^2=T^6=\genfrac{}{}{0ex}{}{V^{max}-V^s}{a^{max}}-T^1$$

$V^s为初始速度；$

下面可以根据位移时间关系方程进行离散化的程序编写。

假设可以到达最大速度，且用户给定了整个过程运行时间$T^f$，则 $T^4$ 的推导如下：
$$\{\begin{array}{l}{T}^f=T^1+T^2+T^3+T^4+T^5+T^6+T^7\\ T^2=T^6\\ T^1=T^3=T^5=T^7\end{array}$$
简化上式可以得到：
$$T^4=T^f-2T^2-4T^1$$
根据 $T^1=\genfrac{}{}{0ex}{}{a^{max}}{J}$代入上式可得：
$$T^4=T^f-2\genfrac{}{}{0ex}{}{v^{max}}{a^{max}}-2\genfrac{}{}{0ex}{}{a^{max}}{J}$$

3.2 $J$ 的推导

这时候还剩下$J$需要计算，通过已量 $T^f,v^{max},a^{max}$可以推导出来；
首先位移之间满足关系如下：
$$S^{ref}=S^a+S^4+S^d$$
其中加速区长度为 $S^a$；
其中减速区长度为 $S^d$；
$$\{\begin{array}{l}{S}^a=v^s(2T^1+T^2)+\genfrac{}{}{0ex}{}{1}{2}J{T}^1(2T^1+3T^1{T}^2+T^2)\\ S^b=v^3(2T^5+T^6)-\genfrac{}{}{0ex}{}{1}{2}J{T}^5(2T^5+3T^5{T}^6+T^6)\end{array}$$
具体推导；²
前面提到过$T^1=T^3=T^5=T^7$，$T^2=T^6$，因此在$V^s$=0的时候，则
$$S^a+S^b=v^3(2T^5+T^6)=v^1(2T^1+T^2)\cdots ④$$

这里简单推导一下：
$$\{\begin{array}{l}{S}^4=v^4{T}^4\\ T^4=T^f-(T^1+T^2+T^3+T^4+T^5+T^6)\\ T^1=T^3=T^5=T^7=\genfrac{}{}{0ex}{}{a^{max}}{J}\\ T^2=T^6=\genfrac{}{}{0ex}{}{V^{max}}{a^{max}}-T^1\\ S^{r}ef=S^a+S^4+S^b\end{array}\cdots ⑤$$
根据④，⑤最终简化得到：
$$J=\genfrac{}{}{0ex}{}{2a^{max}{v}^{max}}{v^{max}{T}^f-v^{max}-S^{ref}{a}^{max}}$$

$T^f$：为运行的总时间
$S^{ref}$：为运行的总路程

4 matlab 程序

matlab程序亲测可以运行，做了简单的修改，
因为这里直接给定了整个运行过程的时间，所以需要在SCurvePara函数中求出加加速度 $J$ 的值，路程$S$为 1：

SCurvePara

 function [Tf1,V,A,J,T] = SCurvePara(Tf, v, a)
 T = zeros(1,7);
for i=1:1000
    % 加加速度 J
    J = (a^2 * v) / (Tf*v*a - v^2 - a);
    % Tk
    T(1) = a / J;
    T(2) = v / a - a / J; % t2 = v / a - t1;
    T(3) = T(1);
    T(4) = Tf - 2 * a / J - 2 * v / a;    % t4 = Tf - 4*t1 - 2*t2;
    T(5) = T(3);
    T(6) = T(2);
    T(7) = T(1);
    % 根据T2和T4判断S曲线的类型
    if T(2) < -1e-6
        a = sqrt(v*J);
        display('t2<0');
    elseif T(4) < -1e-6
        v = Tf*a/2 - a*a/J;
        display('t4<0');
    elseif J < -1e-6
        Tf = (v^2 + a) / (v*a) + 1e-1;
        display('J<0');
    else
        break;
    end
end

 A = a;
 V = v;
 Tf1 = Tf;
 end

SCurveScaling

 function s = SCurveScaling(t,V,A,J,T,Tf)
% J = (A^2 * V) / (Tf*V*A - V^2 - A);
% T(1) = A / J;
% T(2) = V / A - A / J; % T(2) = V / A - T(1);
% T(3) = T(1);
% T(4) = Tf - 2 * A / J - 2 * V / A;    % T(4) = Tf - 4*T(1) - 2*T(2);
% T(5) = T(3);
% T(6) = T(2);
% T(7) = T(1);
%%
if (t >= 0 && t <= T(1))
    s = 1/6 * J * t^3;
elseif (  t > T(1) && t <= T(1)+T(2) )
    dt = t - T(1);
    s = 1/2 * A * dt^2 + A^2/(2*J) * dt...
        + A^3/(6*J^2);
elseif ( t > T(1)+T(2) && t <= T(1)+T(2)+T(3) )
     dt = t - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3) && t <= T(1)+T(2)+T(3)+T(4) )
     dt = t - T(1) - T(2) - T(3);
     s = V*dt ...
         +  (-1/6*J*T(3)^3) + 1/2*A*T(3)^2 + (A*T(2) + A^2/(2*J))*T(3) + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3)+T(4) && t <= T(1)+T(2)+T(3)+T(4)+T(5) )
     t_temp = Tf - t; 
     dt = t_temp - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
     s = 1 - s;
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6) )
     t_temp = Tf - t; 
     dt = t_temp - T(1);
     s = 1/2 * A * dt^2 + A^2/(2*J) * dt + A^3/(6*J^2);
     s = 1 - s;  
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5)+T(6) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6)+T(7) + 1e5 )
     t_temp = Tf - t; 
     s = 1/6 * J * t_temp^3;
     s = 1 - s;     
end
 
end

测试的代码如下：
TEST

%%
N = 500;

ThetaStart = 0;
ThetaEnd = 90;
VTheta = 90;    %1
ATheta = 135;   %1.5
Tf = 1.8;

v = VTheta/(ThetaEnd - ThetaStart);
a = ATheta/(ThetaEnd - ThetaStart);
v = abs(v);
a = abs(a);


Theta = zeros(1,N);
s = zeros(1,N);
sd = zeros(1,N);
sdd = zeros(1,N);

[TF,V,A,J,T] = SCurvePara(Tf, v, a);
display(J, 'J:');
display(TF,'Tf:');
display(V,'v:');
display(A, 'da:');

display(TF-Tf,'dTf:');
display(V-v,'dv:');
display(A-a, 'da:');

t=linspace(0,TF,N);
dt = t(2) - t(1);
for i = 1:N
    if i == N
        a = a;
    end
    s(i) = SCurveScaling(t(i),V,A,J,T,TF);
    Theta(i) = ThetaStart + s(i) * (ThetaEnd - ThetaStart);
    if i>1
        sd(i-1) = (s(i) - s(i-1)) / dt;
    end
    if i>2
        sdd(i-2) = (sd(i-1) - sd(i-2)) / dt;
    end
end

subplot(3,1,1);
legend('Theta');
xlabel('t');
subplot(3,1,1);
plot(t,s)
legend('位移');
xlabel('t');
title('位置曲线');

subplot(3,1,2);
plot(t,sd);
legend('速度');
xlabel('t');
title('速度曲线');

subplot(3,1,3);
plot(t,sdd);
legend('加速度');
xlabel('t');
title('加速度曲线');

看到最终仿真结果和预期相同；

5 总结

本文只对7段的S曲线规划做了详细的推导和介绍，matlab中的程序对于4段和5段都有做实现，很多是在理想情况下进行推导的，初始速度默认为0，终止速度也为0，并且假设加减速区域相互对称。最终运行结果符合预期效果。

文中难免有错误和纰漏之处，请大佬们不吝赐教
创作不易，如果本文帮到了您；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；
请帮忙点个赞 👍👍👍；

6 参考

---

1. 陈友东 魏洪兴 王琦魁.数控系统的直线和 S 形加减速离散算法[D].北京:中国机械工程,2010. ↩︎

2. 郭新贵 李从心 S 曲线加减速算法研究 上海交通大学国家模具 CAD 工程研究中心 , 200030 ↩︎ ↩︎