hdu1325 Is It A Tree?并查集
题目地址
单看题目的话和hdu1272是一样的。但是hdu1272的博文中我也说了,数据比较水,所以我用非并查集的方法就AC了。但是这题的数据没那么水,要用到并查集来解。这题的盲点和重点有这么几个:
- 输入不是以-1 -1结束,而是以两个负数结束
- 需要用并查集来判断是不是只有一个“根”
- 需要判断所有节点的入度是否大于1
- 本题输入的格式,也要注意一下。
可以先忽略图中的方向的。因为如果有环的话,就变成图了,若严格的按照用parent数组来保存上一级父节点的方法,会有冲突。
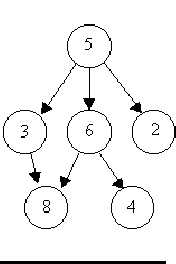
比如这个图中,8的父节点有两个那么parent[8]应该如何存储呢??所以我们可以把它看成无向图,无所谓父子,只需把关系集合merge合并就好了。这种有多个父节点的情况,就使用一个记录入度的数组来标记就好了。
#include<iostream>
using namespace std;
const int MAX=1000;
int rudu[MAX+10];//入度
int parent[MAX+10];
int root[MAX+10];//保存是否为根
bool flag = true;
int r=0;
int getParent(int a)
{
int k=parent[a];
if(parent[a]!=a)
{
parent[a]=getParent(parent[a]);
}
return parent[a];
}
void merge(int a,int b)
{
int p1=getParent(a);
int p2=getParent(b);
if(p1==p2)
return;
parent[p1]=p2;
root[p2]=1;
root[p1]=0;
}
void init()
{
r=0;
flag = true;
for(int i=0;i<=MAX;i++)
{
parent[i]=i;
rudu[i]=0;
root[i]=0;
}
}
void main()
{
int a,b,c=1;
init();
while(cin>>a>>b,a>=0&&b>=0)
{
if(!a&&!b)
{
for(int i=0;i<=MAX;i++)
{
if(rudu[i]>1)
flag = false;
if(root[i])
r++;
}
if(r>1)
flag=false;
if(flag)
cout<<"Case "<<c++<<" is a tree."<<endl;
else
cout<<"Case "<<c++<<" is not a tree."<<endl;
init();
continue;
}
if(getParent(a)!=getParent(b))
merge(a,b);
rudu[b]++;
}
}
 浙公网安备 33010602011771号
浙公网安备 33010602011771号