机器学习入门1.1——线性回归
本文是原创文章,未经博主允许不得转载
我在csdn也同步发表了此文: https://blog.csdn.net/umbrellalalalala/article/details/80217105
本文受众:机器学习零基础者
一、由房价预测问题引出多变量线性回归
我为什么从线性回归开始
理解线性回归是我个人认为的了解机器学习为何物的最好的方式之一,线性回归不需要很难的数学基础。
什么是特征
标题中说的是多变量线性回归,实际上还有单变量线性回归,但后者较为简单,我们稍后会提及
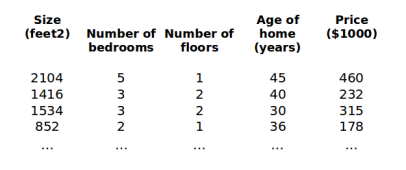
多变量意味着多特征,上图就显示了房价和很多特征的对应关系,这些特征中有房屋面积、卧室数量、楼层数量、房屋年龄。
根据这四个特征,我们来定义特征矩阵:
这个就代表表格中的第一组特征,其中x\(_j^{(i)}\)表示第i组特征的第j个元素,比如x\(_2^{(1)}\) = 5
预测房价
我们在图1中列举了4个已知的房价以及它们的特征,那么我们如何建立房价和特征之间的关系呢?
我们来建立一个参数矩阵:
其中\(θ_1\)~\(θ_4\)对应房价的四个特征,\(θ_0\)是额外加上去的参数,对应偏置量(bias),我们可以先不管它,在后面的学习中我们自然会知道这个是干什么用的
针对本例,我们定义假设函数h_θ(x)如下:
\(h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + θ_3x_3 + θ_4x_4\)
这个函数所计算的就是我们的房价预测值,比如说
y_\(^{(i)}\) = \(h_θ(x^{(i)}) = θ_0 + θ_1x_1^{(i)} + θ_2x_2^{(i)} + θ_3x_3^{(i)} + θ_4x_4^{(i)}\) = \(θ^Tx^{(i)}\)
计算的就是依据第i套房子的特征预测的此套房的价格。
机器学习的目标
现在我们可以讲讲机器学习的目标了,在上一模块,我们提到了房价的预测值y_\(^{(i)}\)的计算方法,
经过计算后,第i组特征值\(x^{(i)}\)对应一个房价预测值y_\(^{(i)}\)和一个真实房价值\(y^{(i)}\),
而机器学习要做的,就是尽量使房价预测值和房价真实值之间的差距减少
笨笨的A:机器学习如何实现房价预测值和真实值之间的差距减少?
聪明的B反问:那你觉得是什么决定了房价的预测值?
笨笨的A答:当然是房子的特征和θ参数矩阵的值
聪明的B再问:那你觉得机器学习能调整哪一项的值?
笨笨的A:我觉得,emmmmm,房子的特征是一定的,机器学习程序只能改变θ的值吧
聪明的B:你也难得聪明一回。机器学习正是通过调整θ参数矩阵的值,从而使得预测值不断地接近真实值的。
机器学习的训练过程:已知一个数据集(比如图1就是一个数据集),数据集中给定了多组(实际上应当是相当多组)特征和真实值之间的对应关系。给θ参数矩阵设置初值,通过假设函数\(h_θ(x)\)计算出预测值,通过不断调整θ参数矩阵的取值,减少预测值和已知的真实值之间的差距。
机器学习的最终成果:一个较好的θ参数矩阵。我们使用这个θ,对房价未知的房子进行预测值的计算。一个好的机器学习成果会较为准确地预测出一个和真实值差距非常小的值
二、★梯度下降算法
为什么从梯度下降算法开始
梯度下降算法是我个人认为的最好的了解机器学习优化算法的方法,它只需要一点点高等数学基础,如果你高等数学学得不太好也没关系,只要你了解梯度就能继续往下看。
(如果你连梯度是什么也不清楚,只要你了解导数,也应该能接受以下的内容,但我要提醒你,数学水平是机器学习的瓶颈之一。但不用担心,如果你只是想早日学会写代码,你可以先”强行理解“这几篇文章的内容。毕竟,不是每个领域的实践都是受限于对理论的了解上的)
注意梯度下降算法只是众多优化算法中的一种
损失函数
顾名思义,预测值和真实值差距越大,损失函数的值越大。
我们定义损失函数如下:
\(J(θ_0,θ_1...θ_n)\) = \(\frac{1}{2m}\sum_{i=1}^m\) \({(h_θx^{(i)}-y^{(i)})}^2\)
显然,本文房价预测的例子的损失函数如下:
\(J(θ_0,θ_1,θ_2,θ_3,θ_4)\) = \(\frac{1}{2×4}\sum_{i=1}^4\) \({(h_θx^{(i)}-y^{(i)})}^2\)
由于本文房价预测的例子中一共给了4组数据,所以上式中m=4,每组数据有4个特征,所以θ参数矩阵中有5个分量。
损失函数J(θ)是关于θ参数矩阵的函数,我们的目标是使得J(θ)的值尽可能小,所以我们采用较为经典的梯度下降算法。
以下我们以一个简单的例子告诉你什么是梯度下降算法
梯度下降算法原理
如果了解梯度可跳过
如果你不知道梯度是什么,那么这部分就是为你准备的,当然你想看完这几行就理解梯度也不太可能(需要你自己再查些梯度定义来了解)
一个简单的例子:
f(x) = \(x^2\)
我们如何求其最小值?
显然,先求其导数,f\(^{'}(x)\) = 2x,
然后,我们求出导数为0的点,即为此函数的极值点,经计算极值点为x=0。
自己画个图分析,无论是向极值点左侧还是向极值点右侧,函数值都是越来越大的,所以x=0为函数的极小值点,所以最小值为f(0)=0。
我们注意到在本例中:
若当前点在极小值点左侧,那么最小值点在当前点的右边;若当前点在极小值点右侧,那么最小值点在当前点的左边
不难证明:
若当前点的导数值为负,那么最小值点在当前点的右边(x轴的正方向);若当前点的导数值为正,那么最小值点在当前点的左边(x轴的负方向)
不难发现,最小值点的方向总是和导数的“方向”是相反的。
以上例子只是一元函数的情况,尚不牵扯梯度的概念,
笨笨的A:啥是梯度呀?
聪明的B:这都不知道,你登过山没?
笨笨的A:登过呀,而且我还发现,朝着最陡峭的方向前进,上升的速度会变快呢
聪明的B:废话,这是常识。而且你刚说的“最陡峭的方向”和“梯度”是一个意思
笨笨的A:6个字的词和2个字的词怎么能是一个意思呢
聪明的B:真拿你没办法。就像沿着最陡峭的方向登山高度上升最快一样,如果某点沿着梯度的方向”前进“,那么此点的函数值也是变大得最快的。
笨笨的A:好吧,我再思考一下。
之后,笨笨的A查阅了一些资料,发现梯度的概念没有想象中那么难。
梯度的方向就是函数值增长最快的方向
以上的例子,我们用导数分析一元函数的最小值,而房价预测的损失函数是一个五元函数,不少机器学习模型的损失函数也为多元函数
所以我们需要用梯度来分析其最小值。使得函数取得最小值的方法就是,沿着梯度的负方向移动(想象一下你下山的时候沿着什么方向下降最快?)
好了,不了解梯度的伙计们,我只能帮你们到这了,毕竟这不是数学博客,剩下的靠你们自己了解了(如果只是想早日写出机器学习程序,可以接着往下看,理论之后再补也不迟)
梯度下降公式
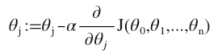
对于θ矩阵中的每一个分量,都分别执行这个公式。
这就是梯度下降算法。
你可能注意到了上式中有一个α,那是学习率,我们在接下来会介绍
学习率
我们在上面已经讲到,沿着梯度的负方向移动当前点是函数值减少最快的方向。但每次移动多少呢?
想象以下下山的时候,我们以最陡峭的方式下山,胆小的(比如你家的泰迪犬)可能会“蹭着”往下走,花了大半天时间才到谷底;胆大的(比如你家的哈士奇)可能跟脱缰的野狗一样拽着你往下死命冲。
学习率就是更新参数的速度,对于梯度下降算法而言,相当于沿着最陡峭的方向下山时,每一步走多远。
泰迪犬花了大半天才到谷底,哈士奇可能半小时就拽着你到了谷底。
那么学习率是不是越大越好呢?当然不是!不过原因并不是哈士奇的速度会把你吓出心脏病。
学习率过大的后果:可能会越过函数局部最小值而导致无法收敛
意思就是:下山时如果你一步迈得太大,以至于你能越过谷底直接一步走到了对面的山峰上,那你就会在山谷间来回“振荡”……
所以,学习率不能过大(越过局部最小值),也不能过小(训练效率低下)
小结
至此,你已经了解到了最基本的线性回归概念,足够你写代码了。
tensorflow官方的第一个程序是mnist手写数字识别程序,是一个分类问题,线性回归似乎无法解决这种问题,所以之后的文章中,我会详细介绍逻辑回归的概念。
但了解那个之前,以下几个问题你能回答吗:
1、机器学习的目标是什么?
2、假设函数\(h_θ{x^(i)}\)是干什么用的?
3、梯度下降算法又被称为“最速下降”,为什么?
4、学习率为什么不能太大?
5、你更喜欢泰迪还是哈士奇?
Enjoy the symphony of the storm. ——umbrellalalalala

