Probability

随机试验:

• 可以在相同条件下重复进行
• 多种可能
• 在实验前不确定是那种结果

样本空间:
随机现象的一切可能基本结果组成的集合称为样本空间

样本点: 样本空间中的一个元素

1. 样本空间中的元素可以是数也可以不是数.
2. 样本空间至少有两个样本点，含两个样本点的样本空间是最简单的样本空间.
3. 从样本空间含有样本点的个数来区分, 样本空间可分为有限与无限两类

随机事件
随机现象的某些样本点组成的集合称为随机事件, 简称事件.常用大写字母A,B,C等表示。如在掷一颗骰子中, A = “出现奇数点”是一个事件, 即 \(A =\{1,3,5\}\)
在以上事件的定义中, 要注意以下几点.

• 任一事件 A 是相应样本空间的一个子集. 在概率论中常用一个长方形表示样本空间 ˝, 用其 中一个圆或其他几何图形表示事件 A, 这类图形称为维恩（Venn）图.
• 当子集 A 中某个样本点出现了, 就说事件 A 发生了, 或者说事件 A 发生当且仅当 A 中某个样本点出现了.
• 事件可以用集合表示, 也可用明白无误的语言描述.
• 由样本空间 ˝ 中的单个元素组成的子集称为基本事件, 而样本空间 ˝ 的最大子集（即 ˝ 本 身）称为必然事件, 样本空间 ˝ 的最小子集（即空集 \(\phi\)）称为不可能事件

随机变量
用来表示随机现象结果的变量称为随机变量, 常用大写字母 X, Y , Z 表示. 很多事件都可用随机变量表示, 表示时应写明随机变量的含义.

概率
概率性质:

\[P(\phi) = 0 \]

• 概率的可加性
  若有限个事件 A1, A2, ..., An 互不相容, 则有
  \[P(\bigcup _{i=1}^n A_{i}) = \sum_{i = 1}^nP(A_{i}) \]

• 概率单调性
  若 \(A \supset B:P(A-B) = P(A)-P(B)\)
  对任意两个事件:A,B则有:\(P(A - B) = P(A) - P(AB)\)
• 概率加法公式
  对任意两个事件 A, B, 有 $ P(A\cup B) = P(A) + P(B) - P(AB) $
  (半可加性). 任意两个事件 A, B, 有 \(P(A\cup B) \le P(A) + P(B)\)
  条件概率:
  所谓条件概率，它是指在某事件 B 发生的条件下, 求另一事件 A 的概率, 记为\(P(A|B)\)

\[P(A|B) = \frac{P(AB)}{P(A)} \]

乘法公式

• 若P(B) > 0，则

\[P(AB) = P(B)P(A|B) \]

• 若\(P(A_{1}A_{2}..A_{n-1}) > 0\),则 \(P(A_{1}...A_{n}) = P(A_{1})P(A_{2}|A_{1})P(A_{3}|A_{2}A_{1}).....P(A_{n}|A_{1}...A_{n-1})\)
  全概率公式
  设B1; B2;.... ; Bn 为样本空间 ˝ 的一个分割(见图 14.2), 即B1; B2; ... ; Bn 互不相容, 且 $\bigcup {i=1}^nB = \Omega \(,如果\)P(B_{i}) > 0,i = 1,2,...n$ 则对任一事件 A 有

\[P(A) = \sum_{i = 1}^n P(B_{i})P(A|B_{i}) \]

贝叶斯公式
设 B1; B2;... ; Bn 是样本空间 \(\Omega\)的一个分割, 即 B1; B2;... ; Bn 互不相
容, 且 $\bigcup {i=1}^nB = \Omega $, 如果 \(P(A) > 0\),$ P(B_{i}) > 0$, \(i=1; 2;... ; n\), 则

\[P(B_{i}|A) = \frac{ P(B_{i})P(A|B_{i}) }{ \sum_{j = 1}^n P(B_{j})P(A|B_{j}) } ,i = 1,2..n \]

独立性
事件 A 发生对 B也无影响，可见独立性是相互的，它们都等价于 \(P(AB) = P(A)P(B)\)
性质: 若事件 A 与 B 独立，则 A 与 \(\overline{B}\) 独立；\(\overline{A}\) 与 B 独立；\(\overline{A}\) 与 \(\overline{B}\) 独立.

多个事件的相互独立
设 A; B; C 是三个事件,如果有
\(P(AB) = P(A)P(B)\) \(P(AC) = P(A)P(C)\) \(P(BC) = P(B)P(C)\) 则A,B,C两两独立，如果还有\(P(ABC) = P(A)P(B)P(C)\),则称A,B,C相互独立.

随机变量
在样本空间\(\Omega\)上的实值函数 \(X = X(w)\) 称为随机变量, 常用大写字母 X; Y; 等表示随机变量, 其取值用小写字母 x,y表示. 假如一个随机变量仅取有限个或可列个值, 则称其为离散随机变量. 假如一个随机变量的可能取值充满数轴上的一个区间,则称其为连续随机变量。
🚗 定义表明：随机变量 X 是样本点w的一个函数, 这个函数可以是不同样本点对应不同的实数, 也允许多个样本点对应同一个实数. 这个函数的自变量（样本点）可以是数, 也可以不是数, 但因变量一定是实数.我们不仅要知道X取哪些值, 而且还要知道它取这些值的概率各是多少, 这就需要分布的概念。

随机变量分布函数
设 X 是一个随机变量, 对任意实数 x, 称

\[F(x) = P(X \leq x) \]

为随机变量 X 的分布函数. 且称 X 服从F(x),记为 \(X \thicksim F(x)\) 有时也可用 \(F(x)\) 以表明是 X 的分布函数.

离散随机变量的概率分布列
设 X 是一个离散随机变量, 如果 X 的所有可能取值是 x1,x2... xn,... 则称 X 取 \(x_{i}\) 的概率

\[p_{i} = p(x_{i}) = P(X = x_{i}),i=1,2,...n... \]

为 X 的概率分布列或简称为分布列, 记为 \(X \thicksim |p_{t}|\) , 分布列也可用如下列表方式来表示：

\[ \left( \begin{array}{cc} x_{1} & x_{2}..\\ p(x_{1}) & p(x_{2})... \end{array} \right) \]

Example: 掷两颗骰子, 其样本空间 \(\Omega\) 含有 36 个等可能的样本点

\[\Omega = \{ (x,y);x,y = 1,2,..6 \} \]

定义如下 3 个随机变量 X; Y 和 Z：

• X 为点数之和, 其可能取值为 2, 3,..12 等共 11 个值
• Y 为 6 点的个数, 其可能取值为 0, 1, 2 等共 3 个值
• Z 为最大点数, 其可能取值为 1, 2, ... 6 等共 6 个值
  分布列的基本性质
  (1) 非负性：\(p(x_{t}) \geq 0,i = 1,2,...\) ;(2) 正则性: $ \sum_{i = 1}^\infty p(x_{i}) = 1 $
  由离散随机变量 X 的分布列很容易写出 X 的分布函数：

\[F(x) = \sum_{x_{1} \leq x} p(x_{i}) \]

几个重要的离散型随机变量:

1. (0-1)分布
   随机变量X只可能取0与1两个值，分布律是
   $ P {X = k} = p^k(1-p),k = 0,1 $
2. 伯努力实验、二项分布
   若实验E只有只有A与\(\overline{A}\) 结果 实验E为伯努力实验(Bernoulli).
   在n次实验中A发生K次的概率为 :
   \[P \{X = k\} = \left( \begin{array}{c} n \\ k \end{array} \right) p^kq^{n-k} ,k = 0,1,2,3...n \]

3. 泊松分布
   设随机变量X所有可能取的值为0,1,2...,而取各个值的概率为
   \[P \{X = k\} = \frac{ \lambda ^k e^{- \lambda} }{k!} ,k = 0,1,2,... \]
   其中\(\lambda > 0\)是常数,则称X服从参数为\(\lambda\)的泊松分布，记为$ X \thicksim \pi (\lambda) $
   泊松定理
   设 $ \lambda > 0\(是一个常数，n是任意正整数，设\) np_{n} = \lambda $,则对于任一固定的非负整数k,有
   \[lim_{n \rightarrow \infty } \left( \begin{array}{c} n \\ k \end{array} \right) p_{n}^k (1-p_{n})^{n-k} = \frac{\lambda ^k e^{-\lambda}}{k!} \]

🚗 也就是以n,p为参数的二项分布概率值可以由参数为$\lambda = np $的泊松分布的概率值来近似。
4. 超几何分布
设有 N 个产品，其中有 M 个不合格品. 若从中不放回地随机抽取 n 个，则其中含有的不合格 品的个数 X 服从超几何分布，记为 \(X\thicksim h(n,N,M)\) 超几何分布的概率分布列为

\[P(X = k) = \frac{ \left( \begin{array}{c} M \\ k \end{array} \right) \left( \begin{array}{c} N-M \\ n -k \end{array} \right) }{\left( \begin{array}{c} N \\ n \end{array} \right)},k = 0,1,...r \]

之中$ r = min {M,n}\( 5. `几何分布` 在伯努利试验序列中，记每次试验中事件 A 发生的概率为 p，如果 X 为事件 A 首次出现时的 试验次数，则 X 的可能取值为 1,2... ，称 X 服从几何分布，记为\) X \thicksim G_{e}(p) $,其分布列为

\[P(X = k) = (1-p)^{k-1}p,k = 1,2... \]

6. 负二项分布(巴斯卡分布)
   在伯努利试验序列中，记每次试验中事件 A 发生的概率为p,如果X为事件A第r次出现时的实验次数,则X的可能取值为r,r+1,..r+m,...,称X服从负二项分布，记做\(X \thicksim Nb(r,p)\),分布列为:
   \[P(X = k) = \left( \begin{array}{c} k-1 \\ r-1 \end{array} \right)p^r(1-p)^{k-r},k = r,r+1,... \]

连续随机变量的概率密度函数

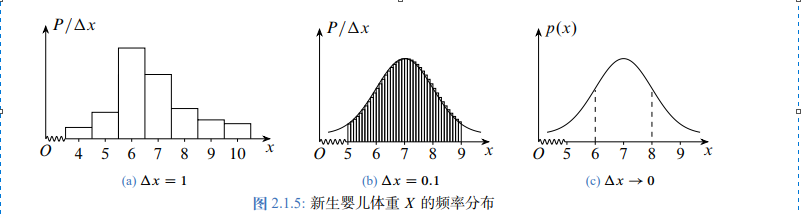
设随机变量 X 的分布函数为\(F(x)\), 如果存在实数轴上的一个非负可积函数 p(x) 使得
对任意实数 x 有

\[F(x) = \int_{-\infty }^x p(t)dt \]

可以看出在\(F(x)\)导数存在的点上都有\(F'(x) = p(x)\),\(F(x)\)是(累积)概率函数，倒数\(F'(x)\)是概率密度函数， 由此可看出p(x) 被称为概率密度函数.

密度函数的基本性质
(1) 非负性: \(p(x) \geq 0\)
(2) 正则性：$ \int_{-\infty}^{+\infty} p(x)dx =1 $

几个重要的连续型随机变量:

1. 均匀分布
   若连续行随机变量X具有概率密度

\[ y = \left\{ \begin{array}{ll} \frac{1}{b-a} & a<x<b \\ 0 & 其他 \end{array} \right. \]

则称X在区间(a,b)上服从均匀分布，记为$ X \thicksim U(a,b) \(,易知\)f(x) \geq 0\(,其\) \int_{-\infty}^{\infty}f(x)dx = 1 $

2. 指数分布
   若连续行随机变量X具有概率密度

\[ y = \left\{ \begin{array}{ll} \frac{1}{ \theta } e^{-x/\theta} & x > 0 \\ 0 & 其他 \end{array} \right. \]

其中\(\theta\) > 0 为常数，则称X服从参数为\(\theta\)的指数分布
3. 正态分布
若连续行随机变量X具有概率密度

\[f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{- \frac{ (x-\mu)^2 }{2 \sigma ^2} } \qquad ,-\infty < x < \infty \]

其中$ \mu,\sigma(\sigma > 0) \(为常数,则称X服从参数为\) \mu,\sigma\(的正态分布或者高斯分布，记做\) X \thicksim N(\mu,\sigma ^2) \(。 特别当\)\mu=0,\sigma = 1$时候称为随机变量X服从标准正态分布

4. 伽马分布
   称一下函数
   $ \Gamma (a) = \int _{0}^{+ \infty} x^{a-1}edx $ 为伽马分布。有一下性质：

   • $ \Gamma(1) = 1,\Gamma(\frac{1}{2}) = \sqrt{\pi} $
   • \(\Gamma(a+1) = a\Gamma(a)\) 当a为自然数n时，有 $ \Gamma(n+1) = n\Gamma(n) = n! $

   若连续行随机变量X具有概率密度

\[ p(x) = \left\{ \begin{array}{ll} \frac{\lambda a}{\Gamma(a)} x^(a-1)e^{-\lambda x} & x \geq 0 \\ 0 & x<0 \end{array} \right. \]

其中a > 0 为形状参数，\(\lambda > 0\)为尺度参数，则称X服从伽马分布，记为$ X \thicksim \Gamma a(a,\lambda) $
5. 贝塔分布
贝塔函数: $ B(a,b) = \int_{0}^{1} x^{a-1}(1-x)dx $,有一下性质:

• B(a,b) = B(b,a)

• 贝塔函数和伽马函数关系 $ B(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} $

  若连续行随机变量X具有概率密度

\[ p(x) = \left\{ \begin{array}{ll} \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^(a-1) (1-x)^{b-1} & 0< x < 0 \\ 0 & 其他 \end{array} \right. \]

其中a > 0,b > 0 为形状参数则称X服从贝塔分布，记为$ X \thicksim Be(a,b) $

随机变量函数分布
一些实验关心的随机变量不是直接测量的到的，而是某个直接测量随机变量的函数，比如要测量园轴横截面的直径d,而我们关心的时候面积\(A = \frac{1}{4}\pi d^2\),随机变量A是随机变量d的函数。已知随机变量X的概率分布去求他的函数\(Y = g(X)\)的概率分布。

🚗设随机变量X具有概率密度 \(f_{X}(x), -\infty <x < \infty\),又设函数g(x)处处可导且恒有 \(g'(x) > 0\) (或者恒有\(g'(x) < 0\)),则\(Y = g(X)\)是连续型的随机变量,其概率密度为

\[ f_{Y}(y) = \left\{ \begin{array}{ll} f_{X}[h(y)]|h'(y)| & a < y < \beta \\ 0 & 其他 \end{array} \right. \]

其中$ a = min{ g(-\infty),g(\infty) }, \beta =max{ g(-\infty),g(\infty) } $,h(y)是g(x)的反函数

多维度随机变量

设E为一个随机实验，它的样本空间是S = {e},设X = X(e)和Y = Y(e)是定义在S上的随机变量，由它们构成一个向量(X,Y) 叫做二维的随机变量或者二维随机向量。不仅与X和Y的性质相关而且依赖与两个随机变量之间的关系

\[F(x,y) = P\{ (X \leq x) \bigcap (Y \leq y) \} \Longleftrightarrow P\{X \leq x,Y \leq y\} \]

成为随机变量(X,Y)的分布函数，或称为随机变量X和Y的 联合分布函数
二维随机变量(X<Y)的分布函数F(x,y),如果存在非负的函数f(x,y)是的任意的x,y,有

\[F(x,y) = \int_{-\infty}^y \int_{-\infty}^x f(u,v)dudv \]

则称(X,Y)为连续型的二维随机变量，函数f(x,y)称为二维随机变量的概率密度或称联合概率密度
有如下性质:

• \(f(x,y) \geq 0\)
• \(\int_{-\infty}^{-\infty}\int_{-\infty}^{-\infty} f(x,y)dxdy = F(\infty,\infty) = 1\)
• 设G是\(xoy\)平面上的区域，点(X,Y)落在G内的概率为
  \[P\{ (X,Y) \} \in G = \int \int _{G}f(x,y)dx,dy \]

• 若f(x,y)在点(x,y)连续，则有

\[\frac{\partial ^2 F(x,y) }{\partial x \partial y} = f(x,y) \]

边缘分布
二维随机变量(X,Y)都有各自的分布函数\(F_{X}(x)\)和\(F_{Y}(y)\),依此称为二维随机变量(X,Y)关于X和Y的边缘分布函数。边缘分布函数可以由(X,Y)的分布函数F(x,y)确定，实际上

\[F_{x}(x) = P\{ X \leq x \} = P\{ X \leq x, Y < \infty \} = F(x,\infty) \]

即 $$ F_{X}(x) = F(x,\infty) $$

对于离散型随机变量,

\[F_{X}(x) = F(x,\infty) = \sum_{x_{i} \leq x} \sum_{j = 1}^{\infty} p_{ij} \]

知道X的 分布律 为

\[P\{ X = x_{i} \} = \sum_{j = 1} ^ \infty p_{ij}, \qquad i = 1,2,... \]

记 $ p_{i \cdot } = \sum_{j = 1}^{\infty} p_{ij} = P{ X =x_{i} }, \qquad i = 1,2,3$ 为(X,Y)关于X和Y的边缘分布律.注意此处$ p_{i \cdot }$有个点哦。

对于连续型随机变量(X,Y)，它的概率密度为f(x,y),由于

\[F_{X}(x) = F(x,\infty) = \int_{-\infty}^x [ \int_{-\infty}^{\infty} f(x,y)dy]dx \]

X是一个连续的随机变量，且概率密度为$f_{X}(x) = \int_{-\infty}^{\infty}f(x,y)dy \(,同样Y的概率密度为 \) f_{Y}(y) = \int_{-\infty}^{\infty}f(x,y)dx \( 分别称\)f_{X}(x)\(和\)f_{Y}(y)$为(X,Y)关于X和关于Y的边缘概率密度

条件分布
设(X,Y)是二维离散型随机变量,对于固定的j,若\(P\{Y = y_{j} \} > 0\),则称
$$ P{X = x_{i} | Y = y_{i}} = \frac{ P{X = x_{i},Y =y_{i} } }{ P{Y=y_{i}} } = \frac{p_{ij}}{p_{i \cdot}},j = 1,2... $$ 为\(Y=y_{j}\)条件下随机变量X的条件分布律

设二维随机变量(X,Y)的概率密度为f(x,y),(X,Y)关于Y的边缘概率密度为\(f_{Y}(y)\),若对于固定的y,\(f_{Y}(y) > 0\),则称$\frac{f(x,y)}{f_{Y}(y)} $在Y= y的条件下X的 条件概率密度 ,记为

\[f_{X|Y}(x|y) = \frac{f(x,y)}{f_{Y}(y)} \]

称$ \int_{-\infty}^x f_{X|Y}(x|y)dx = \int_{-\infty}^x \frac{f(x,y)}{f_{Y}(y)}dx $ 在Y= y的条件下X的条件分布函数，记作$P = { X \leq x , Y \leq y} $或者 $ F_{X | Y}(x|y) $

相互独立的随机变量

设F(x,y)及\(F_{X}(x)\),\(F_{Y}(y)\)是分别二维随机随机变量(X,Y)的分布函数及边缘分布函数。若对于所有的x,y都有

\[P\{ X \leq x,Y \leq y \} = P\{X \leq x\}P\{Y \leq y\} \]

即 $ F(x,y) = F_{x}(x)F_{Y}(y) $ 则称随机变量X,Y为相互独立的

设(X,Y)为连续型随机变量，f(x,y),f_{X}(x)及f_{Y}(y)分别为(X,Y)的概率密度和边缘概率密度，则X和Y 相互独立的条件等价与 $ f(x,y) = f_{X}(x)f_{Y}(y) $

设(X,Y)为离散型随机变量,则X和Y 相互独立的条件等价对于所有可能取值(x_{i},y_{i})都有 $ P{ X = x_{i},Y = y_{i} } = P{X = x_{i}}P{ Y = y_{i} } $

两个随机变量的函数的分布

• Z = X+Y 的分布

设(X,Y)为连续型二维随机变量，它具有概率密度为f(x,y),则Z = X+Y仍为连续型随机变量，其概率密度为

\[f_{X+Y}(z) = \int_{-\infty}^{\infty} f(z-y,y)dy \qquad \qquad f_{X+Y}(z) = \int_{\infty}^{\infty} f(x,z - x)dx \]

若X和Y是相互独立的，则 $ f_{X+Y}(z) = \int_{-\infty}^{\infty} f_{X}(z - y)f_{Y}(y)dy \qquad \qquad f_{X+Y}(z) = \int_{-\infty}^{\infty} f_{X}(x)f_{Y}(z - x)dy \(,这两个公式为\)f_{X}\(和\)f_{Y}\(的`卷积公式`,记作\) f_{X} \ast f_{Y} $

一般，设X,Y相互独立且$ X \thicksim N(\mu_{1},\sigma_{1}^2)\(,\) Y \thicksim N(\mu_{2},\sigma_{2}^2)\(,则Z = X + Y仍然服从正态分布,且有\) Z \thicksim N(\mu_{1} + \mu_{2},\sigma_{1}^2 + \sigma_{2}^2)$，可以推广到n个相互对立的正态随机变量之和的情况。

• \(Z= \frac {Y}{X}\) 的分布、Z = XY的分布
  设(X,Y)为连续型二维随机变量，它具有概率密度为f(x,y),则$ Z = \frac{Y}{X}\(、\)Z = XY$仍未连续型随机变量、其概率密度分别为

\[ f_{Y/X}(z) = \int_{-\infty}^{\infty}|x|f(x,xz)dx \\ f_{XY}(z) = \int_{-\infty}^{\infty} \frac{1}{|x|} f(x,\frac{z}{x})dx \]

又若X和Y相互独立，设(X,Y)关于X,Y的边缘密度分别为f_{X}(x),f_{Y}(y)则变为

\[ f_{Y/X}(z) = \int_{-\infty}^{\infty}|x| f_{X}(x) f_{Y}(xz)dx \\ f_{XY}(z) = \int_{-\infty}^{\infty} \frac{1}{|x|} f_{X}(x)f_{Y}(\frac{z}{x})dx \]

• M = max{X,Y}和N = min{X,Y}
  设X,Y是两个相互独立的随机变量，它们的分布函数分别为\(F_{X}(x)\)和\(F_{Y}(y)\),则相互独立的X和Y
  $ F_{max}(z) = P{ M \leq z } = P{ X \leq z,Y \leq z } = p{ X \leq z }P{ Y \leq z } $则有 \(F_{max}(z) = F_{X}(z)F_{Y}(z)\)
  类似的
  $F_{min}(z) = P { N \leq z } = 1 - P{ N > z} =1-P{ X > z,Y > z } = 1 - P{ X > z } \cdot P{ Y > z } $
  即 $ F_{min}(z) = 1- [1 - F_{X}(z)][1- F_{Y}(z)] $