Game Physics

Basic concepts form physics

Rigid Body Classification

Single particles and particles system are examples of discrete material. The standard notation is

\[Q_{total} = \sum\limits_{i=1}^{p}Q_{i} \]

Another type of body is referred to as a continuous material,consisting of infinitely many particles that lie in a bounded region of space,denoted \(R\).This rigid body as a continuum of mass.

Various physical quantities involve summations over all particles of mass in the region.

\[Q_{total} = \int_{R} Q dR \]

where \(R\) is the region, \(dR\) is an infinitesimal portion of the region, and \(Q\) is the physical quantity of interest and can be scalar- or vector-valued.

PlanarMotion in Cartesian Coordinates

First let us consider when the particle motion is constrained to be planar. In Cartesian coordinates, the position of the particle at time t is

\[r(t) = x(t)i + y(t)j \]

where \(i = (1,0)\) and \(j = (0,1)\).The velocity of the particle at time is

\[v(t) = \dot{r} = \dot{x}i + \dot{y}j \]

The acceleration of the particle at time t is

\[a(t) = \dot{v} = \ddot{r} = \ddot{x}i + \ddot{y}j \]

At each point on the curve of motion we can define a unit-length tangent vector by normalizing the velocity vector

\[T(t) = \frac{v}{|v|} = (cos(\phi(t)),sin(\phi(t))) \]

A unit-length normal vector

\[N(t) = (-sin(\phi(t)),cos(\phi(t))) \]

The coordinate system{ $ r(t ); T(t ),N(t ) $ } is called a moving frame.

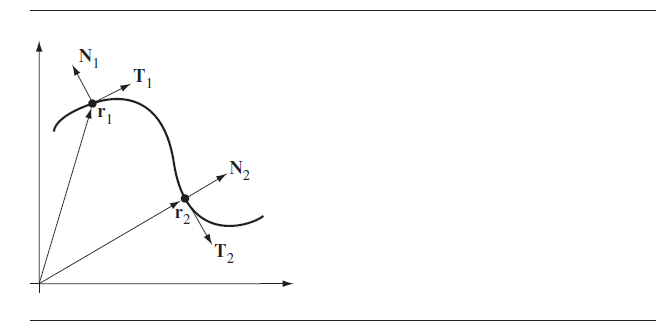
\(v = |v|T = \dot{s}T\) \(a = \dot{v} = \frac{d}{dt}(\dot{s}T) = \ddot{s}T + \dot{s}\frac{dT}{dt} = \ddot{s}T + \ddot{s}^2\frac{dT}{ds}\)

\(\frac{dT}{ds} = \frac{d}{ds}(cos\phi,sin\phi) = \frac{d\phi}{ds}(-sin\phi,cos\phi) = \kappa N(s)\) where \(\kappa = \frac{d\phi}{ds}\) is the curvature ofht e curve at arc length s. The acceleration is therefore

\[a = \ddot{s}T + \kappa \dot{s}^2N \]

The component \(\ddot{s}T\) is called the tangential acceleration.The component \(\kappa\dot{s}^2N\) is called the normal acceleration or centripetal acceleration

\[\kappa = \frac{v \cdot a^{\bot}}{ |v|^3 } = \frac{\dot{x}\ddot{y} - \dot{y}\ddot{x}}{(\dot{x}^2 + \dot{y}^2)^{3/2}} \]

$\frac{dN}{ds} = \frac{d}{ds}(-sin\phi,cos\phi) = \frac{d\phi}{ds}(-cos\phi,-sin\phi) = - \kappa T $

\[ J=m\begin{bmatrix} \frac{dT}{ds} \\ \frac{dN}{ds} \end{bmatrix} = \begin{bmatrix} 0 & \kappa \\ -\kappa & 0 \end{bmatrix}\begin{bmatrix} T \\ N \end{bmatrix} \qquad \qquad \qquad (12.30)\]