Rotational Dynamics

12.5 Rotational Dynamics

Rotational Kinematics

For Rotational kinematics ,The analog of linear velocity and acceleration are called angular velocity and angular acceleration.We denote them as \(\mathbf{w(t)}\) and \(\mathbf{a(t)}\). Two slightly different types of angular velocity.

• spin angular velocity
  Spin angular velocity describes the rate of change of orientation of an object and is not affected by translation of the object.
• orbital angular velocity
  Orbital angular velocity is actually not concerned with orientation at all; instead, it measures the rate at which the position of an object traces out an orbit around some other point.

\(\hat{n}\) tells us the direction of th axis,\(\omega\) is the radians per unit time ,the the spin angular velocity fo the rigid body by the angular velocity vector \(\mathbf{w}\)(not the blodface) : \(\mathbf{w}\) \(= \omega\hat{n}\)

When talking about orbital angular velocity, we must be clear about what point o we are measuring the angular velocity relative to. We do not measure the orbital angular velocity relative to the center of mass \(c\) ! We measure the orbital angular velocity relative to the point that is actually being orbited, and only those points on the “equator” of the object are actually orbiting around \(c\). Given any other arbitrary point, it will orbit a
point \(o\) that lies on the axis of rotation, as shown in Figure 12.16.( 就是当我们讨论orbital angular veloctiy的时候，我把必须清楚的一点是:oribital anugular velocity是相对那个点来进行旋转的，我们并不是相对与质心\(c\) ,而是他实际所绕的那个点\(o\)，这个点是在axis of rotatoin上的。只有"equator" of the object上的这些点才会绕这质心\(c\)进行旋转 )

consider the dynamics of rotation:

右图中，By applying Newton’s second law, we can compute the magnitude of the tangential acceleration (此处是切线的速度并不是角速度)as $$a_{\bot} = F_{\bot}/m$$

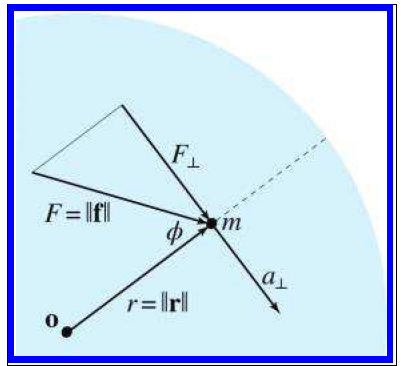
the relationship between linear speed and angular velocity: $v_{\bot} = s = r\mathbf{w} $, 这样 $ \dot{v_{\bot}} = r\dot{\mathbf{w}}$ 得出: \(a_{\bot} = r\mathbf{a}\)==> $$\mathbf{a} = a_{\bot} / r$$

如图所示: But in general, mass is distributed around the disk, so there are many m’s and r’s. This “cause” of angular acceleration is known as torque, which we denote by using the Greek letter \(\tau\) .

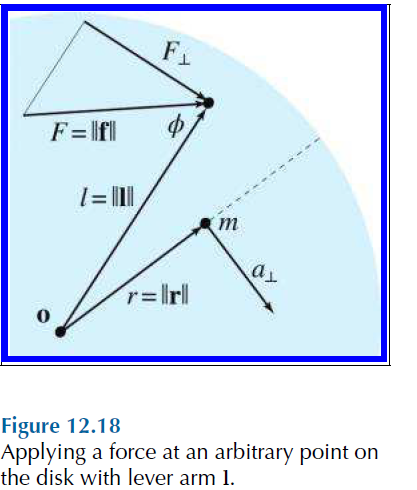
we can state this succinctly by: \(\tau = Flsin \phi\). The dimensions of torque are not the same as force. Torque has units of “force times length.”

In summary, the moment of inertia of an object, which must be measured relative to some particular pivot (in this case, it’s the fixed pivot point, but for a rigid body we usually measure it relative to its center of mass), quantifies the degree to which the object will resist angular acceleration about that pivot. The moment of inertia J of a point mass is proportional to its mass and proportional to the square of the distance from the mass to the pivot.

Moment of Inertia of a Point Mass in the Plane

\[J = mr^{2} \]

Now imagine that the disk in our thought experiment has multiple masses placed on it. Each of these masses contributes to the disk’s resistance to rotation, and their contribution is the same, regardless of where any force is applied. To compute the moment of inertia of an arbitrary rigid body, we **break up the object into “mass elements” such that for each element we know the mass \(m_{i}\) and radial distance to the center of mass \(r_{i}\) **. We then sum up the moments of inertia of each individual mass element:

\[J = \sum\limits_{i}J_{i} = \sum\limits_{i}m_{i}r^2 \]

Rotational Equivalent of Newton’s Second Law:

\[\tau = Ja \]

For rotation in a plane, all of the variables in Equation (12.26) are scalars. In three dimensions, however, \(\tau\) and \(a\) become vector quantities, and \(J\) becomes a matrix.

We’ve considered torque, the rotational analog to linear force. Now let’s turn our attention to momentum. Remember that linear momentum is the “quantity of motion” contained in an object. Its analog, angular momentum, has a similar interpretation. Intuitively, angular momentum describes how hard it will be to stop the rotation of the object. If the angular momentum is large, then the magnitude of the applied torque, or the duration for which it is applied, or both, must be large.

Spin Angular Momentum:

Angular momentum (\(L\)) is the product of the moment of inertia \(J\) and angular velocity (\(ω\)):

\[L = Jω \]

A similar relationship exists between angular momentum and torque. As torque is applied over time, it builds up angular momentum; equivalently, torque is equal to the rate of change (derivative) of angular momentum. As with linear momentum, this can be interpreted as a conservation law.

Torque and the Conservation of Angular Momentum：

\[L = \int\tau dt \qquad \qquad \qquad \tau = \frac{dL}{dt} \]

3D Rotational Dynamics

To extend the dynamics principles into three dimensions, we start with torque denoted by \(\tau\) .and
the direction of this vector indicates the axis about which the torque is tending to induce rotation. The formula for computing the torque for an applied force \(f\) and lever arm \(l\) is actually simpler in 3D than the corresponding 2D formula!

Torque in Three Dimensions

\[\tau = l \times f \]

Angular momentum likewise becomes a vector \(L\), with a similar formula for its relation to the linear quantity:\(L = r \times P\).

Inertia Tensor
The inertia tensor of a mass \(m\) with radial vector \(r\) is:

\[ J=m\begin{bmatrix} r_{y}^2 + r_{z}^2 & -r_{y}r_{x} & -r_{z}r_{x} \\ -r_{x}r_{y} & r_{z}^2 + r_{x}^2 & -r_{z}r_{y} \\ -r_{z}r_{x} & -r_{y}r_{z} & r_{x}^2 + r_{y}^2 \end{bmatrix} \qquad \qquad \qquad (12.30)\]

In three dimensions we sometimes refer to the moment of inertia as the inertia tensor.

3D Rotational Analog of Newton’s Second Law \(\tau = αJ\). ==> \(a = \tau J^{-1}\)

Equation (12.30) tells us how to compute the inertia tensor for a point mass, but what about more complicated shapes?In a manner similar to how we computed the center of mass, we can imagine breaking up a compound object into a large number of mass elements and taking the sum of their individual moments of inertia. Taking the limit as the volume of the largest element approaches zero, this sum becomes a multidimensional integral. Such integrals are typically difficult or impossible to solve analytically, except for abstract primitives such as boxes, disks, cylinders, spheres,cones, and the like. Fortunately, such primitives arise commonly in practice and can make adequate approximations. Even more fortunate for us is the fact that the hard work of solving the integral has already been done for a large variety of primitives. For such primitives, the best method for obtaining the moment of inertia is to look up the formula in a table.

Collision Response with Rotations

Remember the basic strategy:

• Compute the relative velocities at the point of contact.
• Project the relative velocities onto the surface normal. This is the velocity that must be counteracted in order to prevent (further) penetration.
• Compute k, the magnitude of an impulse, such that when we apply the impulse to both objects (in opposite directions) parallel to the surface normal, the post-collision velocities, measured along the surface normal, have the desired magnitude according to some collision law. This discussion will be based upon Newton’s collision law and the coefficient of restitution e.
• Apply the impulse \(kn\) to one object and \(−kn\) to the other.

Dealing with objects that can rotate adds a few complications.First, we earlier referred to “the” velocity of an object. But when an object is rotating, the different points on the object have different linear velocities.The velocity we need is not the velocity of the object’s center of mass, but rather the velocity at the point of contact. So we must extend our velocity calculation to account for the angular velocity. Likewise, our prediction of the post-impulse velocities at the points of impact must also take into consideration rotational effects. Application of an impulse at the point of contact will create an angular impulse, which will change the rate of rotation. In general, when objects are free to rotate, a smaller impulse will suffice to resolve the collision, since the impulse has two ways by which to reduce the point velocities. The change in angular velocity will cause the points of contact to move away from each other faster than their centers of mass do. Indeed, the centers of mass may still be moving towards each other after the collision.

In line dynamics we have: \(v'_{rel} \cdot n= -e v_{rel}\cdot n\),通过这种方式计算magnitude of the impulse(\(k\)).现在也可以这样计算:
We use \(r_{i}\) to denote the position of the point of impact on object i relative to its center of mass, \(ω_{i}\) for the angular velocity of the object, \(m_{i}\) for the mass, and \(J_{i}\) for the inertia tensor. For linear velocity, we need to introduce some new notation to distinguish between the linear velocities at the point of contact, which we denote as \(u_{i}\), and the linear velocities of the center of mass, denoted \(v_{i}\). As before, primes on the quantities refer to their values after the collision.

compute the point velocity of each object

\[u_{1} = v_{1} + w_{1}\times r_{1} \qquad u_{2} = v_{2} + w_{2}\times r_{2} \]

The velocities after the collision depend on the change in linear velocity of the center of mass, and also the change in angular velocity. These are computed by

\[v'_{1} = v_{1} - kn/m_{1} \qquad v'_{2} = v_{2} + kn/m_{2} \\ w'_{1} = w_{1} − (r_{1} × kn)J_{1}^{-1} \qquad w'_{2} = w_{2} + (r_{2} × kn)J_{2}^{-1} \]