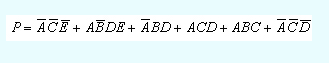卡诺图简单逻辑化简与五变量卡诺图化简
一、格雷码编码规则
画卡诺图的时候需要先将所有变量可能以格雷码的形式排列在方格两侧，所有变量有2^n个，虽然我们常用的变量为四个及以下，可以熟记格雷码，但为了学习还是有必要了解格雷码的编码规则。格雷码的基本特点就是任意两个相邻的代码只有一位二进制数不同，这样在数字电路中变化时每次就只有一位发生变化，提高了电路的稳定性。
规则：
自然二进制数到格雷码： 保留二进制码的最高位作为格雷码的最高位，而次高位格雷码为二进制码的高位与次高位相异或，而格雷码其余各位与次高位的求法相类似。
格雷码到自然二进制数：保留格雷码的最高位作为自然二进制码的最高位，而次高位自然二进制码为高位自然二进制码与次高位格雷码相异或，而自然二进制码的其余各位与次高位自然二进制码的求法相类似。
以一个四位二进制数来举例，二进制（abcd）,依据规则转换为格雷码就是【a, (a^b), (b^c), (c^d)】， 依据规则继续转化二进制的话就是 【a, (a^a^b), (a^a^b^b^c), (a^a^b^b^c^c^d)】，化简之后仍然可以得到（abcd）。
二、卡诺图简单逻辑化简
逻辑化简的实际目标是尽可能地减少表达式中包含的项数以及各项包含的变量数。
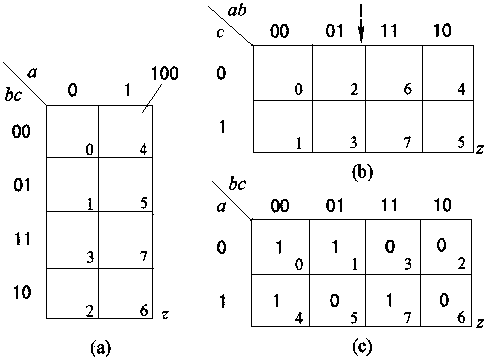此图即为基本卡诺图的形式，如何画就不在赘述，两侧变量依据格雷码形式，目的就是画卡诺圈将里面的1全都包括在内，卡诺圈尽量大，卡诺圈的数量尽量少。
（a）卡诺图上处在相邻、相对、相重位置的小方格所代表的最小项为相邻最小项。
（b）两个小方格相邻, 或处于某行(列)两端时，所代表的最小项可以合并，合并后可消去一个变量。
(c) 四个小方格组成一个大方格、或组成一行（列）、或处于相邻两行（列）的两端、或处于四角时，所的表的最小项可以合并，合并后可消去两个变量。
(d) 八个小方格组成一个大方格、或组成相邻的两行（列）、或处于两个边行（列）时，所代表的最小项可以合并，合并后可消去三个变量。
对于方格中带有未知变量x的，是可圈可不圈的，依据自己实际情况而定。
五变量卡诺图化简：
五变量以下最多十六方格，可轻易用上述方法得到。六变量以上方格过多，用此方法反倒麻烦。我也是通过找资料学习这两个变量的化简方法，分享给大家。习惯上我们会自然而然的将五变量分为二变量和三变量写在方格的两侧，可有时上述规则就会变得并不适用。比如下面这个例子。
| ab\cde | 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
| 00 | ||||||||
| 01 | 1 | 1 | 1 | 1 | ||||
| 11 | ||||||||
| 10 |
化简之后并不能够消去两个变量，只能消去一个变量。六变量卡诺图化简也存在可能出现这些问题。
五变量卡诺图化简
它是由四变量最小项图构成的，将左边的一个四变量卡诺图按轴翻转 180 °而成。左边的一个四变量最小项图对应变量 E =0 ，轴左侧的一个对应 E =1 。这样一来除了几何位置相邻的小方格满足邻接条件外，以轴对称的小方格也满足邻接条件，这一点需要注意。图中最小项编号按变量高低位的顺序为 EABCD 排列时，所对应的二进制码确定。
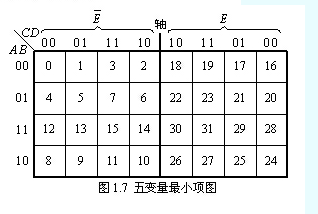
此时要注意列上变量排列的左右对称关系，对于既不含 E非也不含 E 的与项，可以填入 E非四变量卡诺图中然后以中间轴翻转 180 °，在 E 四变量卡诺图中对称位置也填上“ 1 ”。举例说明如下。
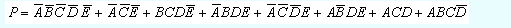
上面那句话比较抽象，
意思如图所示。
