PID调节
较好的参考
一般使用增量式PID算法,比位置式pid算法计算简单,内存消耗小,计算机输出的是控制机构的增量,即
实际控制量=上次控制量+PID算法输出值
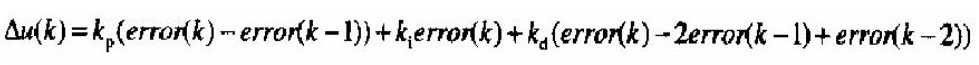


以上才是有营养的东西
----------------
-----------------
以下全是废话,垃圾资料浪费人生
PID是什么
始于1936 年2 月17 日,不用考虑被控对象的数学模型就能调节控制被控对象的一种方法 。PID,就是对输入偏差进行比例积分微分运算,运算的叠加结果去控制执行机构。
什么是PID?P就是比例就是输入偏差乘以一个系数;I 就是积分,就是对输入偏差进行积分运算;D 就是微分,对输入偏差进行微分运算。浅白一点说,就是先把系统调为纯比例作用,然后增强比例作用让系统震荡,记录下刚出现震荡时的比例作用Km和震荡周期T(T=2π/ω),根据下面的式子就可以得到P参数、I参数、D参数(一般情况)
Kp = 0.6*Km
Kd = Kp*π/4*ω
Ki = Kp*ω/π
就像你走路不需要精确知道你每一步走多远,却可以走到目的地一样
基本的PID调节器有两个输入值,被调量和设定值。一般来说,被调量是随系统状态在变化的,设定值是人们期望系统达到的一个固定值。基本的PID调节器还有一个输出量去控制执行机构
在我看来PID调节器就是程序里的一个函数,所谓的调PID就是在调节P参数、I参数、D参数
P 纯比例作用分析
P是比例作用,把调节器的输入偏差乘以P参数,结果作为调节器的输出。
输出=偏差*Kp
所以输出有和偏差类似的形状,得出以下结论,即
对于正作用的调节系统,顶点、谷底均发生在同一时刻。对于负作用的调节系统,被调量的顶点就是输出的谷底,谷底就是输出的顶点。波动周期完全一致。只要被调量变化,输出就变化;被调量不变化,不管静态偏差有多大,输出也不
会变化。
I 纯积分作用分析
如何科学地整定PID?
收集数据画曲线:
* 1 设定值(一般是条直线)
* 2 被调量的波动曲线
* 3 PID的输出曲线
如果是串级调节系统,我们还要收集:
* 4 副调的被调量曲线
* 5 PID 输出曲线
为什么不收集副调的设定值了?因为主调的输出就是副调的设定啊。在一个比较复杂的
调节系统中,副调的被调量往往不只一个,那就有几个收集几个。
PID整定方法,主要是靠玄学的经验试凑法,耗费大量时间去根据经验猜、调
把P、I、D 隔离开来。先去掉积分、微分作用,让系统变为纯比例调节方式。然后
再考虑积分,然后再考虑微分。
整定比例作用比较笨的办法,先把系统设置为纯比例作用,也就是说积
分时间无穷大,微分增益为0。逐渐加大比例作用,一直到系统发生等幅震荡,然后在这
个基础上适当减小比例作用即可,或者把比例增益乘以0.6~0.8。怎么判断震荡呢?一般来说,对于一个简单的单回路调节系统,比例作用很强的时候,振荡周期是很有规律的,基本上呈正弦波形状。。
参数整定找最佳, 从小到大顺序查。
先是比例后积分, 最后再把微分加。
曲线振荡很频繁, 比例度盘要放大。
曲线漂浮绕大弯, 比例度盘往小扳。
曲线偏离回复慢, 积分时间往下降。
曲线波动周期长, 积分时间再加长。
曲线振荡频率快, 先把微分降下来。
动差大来波动慢, 微分时间应加长。
理想曲线两个波, 前高后低四比一。
一看二调多分析, 调节质量不会低。
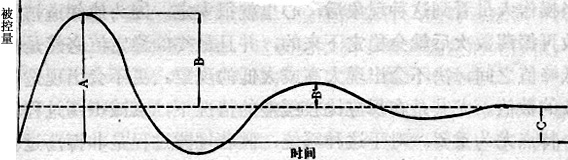
衡量一个PID控制系统质量的好坏,主要是看在外界干扰产生后,被控量偏离给定值的情况,假如偏离了以后能很快的平稳的回复到给定值,就认为是好的。通常认为图2所示的过渡过程是最好的,并以此作为衡量PID控制系统的质量指标。选用这个曲线作为指标的理由是:因为它第一次回复到给定值较快,以后虽然又偏离了,但是偏离不大,并经过几次振荡就稳定下来了,定量的看:第一个波峰B的高度是第二个波峰B'高度的四倍,所以这种曲线又叫做4:1衰减曲线。在调节器的工程参数整定时,以能得到4:1的衰减过渡过程为最好,这时的PID控制参数可叫最佳参数。 “理想曲线两个波,前高后低4比1”就是指图2这样的曲线,也就是过渡过程振荡两次就能稳定下来,并且振荡两次后有约近于4:1的衰减比,它被认为是最好的过渡过程。
PID 算法示例
#include <reg52.h>
typedef unsigned char uChar8;
typedef unsigned int uInt16;
typedef unsigned long int uInt32;
sbit ConOut = P1^1; //加热丝接到P1.1口
typedef struct PID_Value
{
uInt32 liEkVal[3]; //差值保存,给定和反馈的差值
uChar8 uEkFlag[3]; //符号,1则对应的为负数,0为对应的为正数
uChar8 uKP_Coe; //比例系数
uChar8 uKI_Coe; //积分常数
uChar8 uKD_Coe; //微分常数
uInt16 iPriVal; //上一时刻值
uInt16 iSetVal; //设定值
uInt16 iCurVal; //实际值
}PID_ValueStr;
PID_ValueStr PID; //定义一个结构体,这个结构体用来存算法中要用到的各种数据
bit g_bPIDRunFlag = 0; //PID运行标志位,PID算法不是一直在运算。而是每隔一定时间,算一次。
/* ********************************************************
/* 函数名称:PID_Operation()
/* 函数功能:PID运算
/* 入口参数:无(隐形输入,系数、设定值等)
/* 出口参数:无(隐形输出,U(k))
/* 函数说明:U(k)+KP*[E(k)-E(k-1)]+KI*E(k)+KD*[E(k)-2E(k-1)+E(k-2)]
******************************************************** */
void PID_Operation(void)
{
uInt32 Temp[3] = {0}; //中间临时变量
uInt32 PostSum = 0; //正数和
uInt32 NegSum = 0; //负数和
if(PID.iSetVal > PID.iCurVal) //设定值大于实际值否?
{
if(PID.iSetVal - PID.iCurVal > 10) //偏差大于10否?
PID.iPriVal = 100; //偏差大于10为上限幅值输出(全速加热)
else //否则慢慢来
{
Temp[0] = PID.iSetVal - PID.iCurVal; //偏差<=10,计算E(k)
PID.uEkFlag[1] = 0; //E(k)为正数,因为设定值大于实际值
/* 数值进行移位,注意顺序,否则会覆盖掉前面的数值 */
PID.liEkVal[2] = PID.liEkVal[1];
PID.liEkVal[1] = PID.liEkVal[0];
PID.liEkVal[0] = Temp[0];
/* =================================================================== */
if(PID.liEkVal[0] > PID.liEkVal[1]) //E(k)>E(k-1)否?
{
Temp[0] = PID.liEkVal[0] - PID.liEkVal[1]; //E(k)>E(k-1)
PID.uEkFlag[0] = 0; //E(k)-E(k-1)为正数
}
else
{
Temp[0] = PID.liEkVal[1] - PID.liEkVal[0]; //E(k)<E(k-1)
PID.uEkFlag[0] = 1; //E(k)-E(k-1)为负数
}
/* =================================================================== */
Temp[2] = PID.liEkVal[1] * 2; //2E(k-1)
if((PID.liEkVal[0] + PID.liEkVal[2]) > Temp[2]) //E(k-2)+E(k)>2E(k-1)否?
{
Temp[2] = (PID.liEkVal[0] + PID.liEkVal[2]) - Temp[2];
PID.uEkFlag[2]=0; //E(k-2)+E(k)-2E(k-1)为正数
}
else //E(k-2)+E(k)<2E(k-1)
{
Temp[2] = Temp[2] - (PID.liEkVal[0] + PID.liEkVal[2]);
PID.uEkFlag[2] = 1; //E(k-2)+E(k)-2E(k-1)为负数
}
/* =================================================================== */
Temp[0] = (uInt32)PID.uKP_Coe * Temp[0]; //KP*[E(k)-E(k-1)]
Temp[1] = (uInt32)PID.uKI_Coe * PID.liEkVal[0]; //KI*E(k)
Temp[2] = (uInt32)PID.uKD_Coe * Temp[2]; //KD*[E(k-2)+E(k)-2E(k-1)]
/* 以下部分代码是讲所有的正数项叠加,负数项叠加 */
/* ========= 计算KP*[E(k)-E(k-1)]的值 ========= */
if(PID.uEkFlag[0] == 0)
PostSum += Temp[0]; //正数和
else
NegSum += Temp[0]; //负数和
/* ========= 计算KI*E(k)的值 ========= */
if(PID.uEkFlag[1] == 0)
PostSum += Temp[1]; //正数和
else
; /* 空操作。就是因为PID.iSetVal > PID.iCurVal(即E(K)>0)才进入if的,
那么就没可能为负,所以打个转回去就是了 */
/* ========= 计算KD*[E(k-2)+E(k)-2E(k-1)]的值 ========= */
if(PID.uEkFlag[2]==0)
PostSum += Temp[2]; //正数和
else
NegSum += Temp[2]; //负数和
/* ========= 计算U(k) ========= */
PostSum += (uInt32)PID.iPriVal;
if(PostSum > NegSum) //是否控制量为正数
{
Temp[0] = PostSum - NegSum;
if(Temp[0] < 100 ) //小于上限幅值则为计算值输出
PID.iPriVal = (uInt16)Temp[0];
else PID.iPriVal = 100; //否则为上限幅值输出
}
else //控制量输出为负数,则输出0(下限幅值输出)
PID.iPriVal = 0;
}
}
else PID.iPriVal = 0; //同上,嘿嘿
}
/* ********************************************************
/* 函数名称:PID_Output()
/* 函数功能:PID输出控制
/* 入口参数:无(隐形输入,U(k))
/* 出口参数:无(控制端)
******************************************************** */
void PID_Output(void)
{
static uInt16 iTemp;
static uChar8 uCounter;
iTemp = PID.iPriVal;
if(iTemp == 0)
ConOut = 1; //不加热
else ConOut = 0; //加热
if(g_bPIDRunFlag) //定时中断为100ms(0.1S),加热周期10S(100份*0.1S)
{
g_bPIDRunFlag = 0;
if(iTemp) iTemp--; //只有iTemp>0,才有必要减“1”
uCounter++;
if(100 == uCounter)
{
PID_Operation(); //每过0.1*100S调用一次PID运算。
uCounter = 0;
}
}
}
/* ********************************************************
/* 函数名称:PID_Output()
/* 函数功能:PID输出控制
/* 入口参数:无(隐形输入,U(k))
/* 出口参数:无(控制端)
******************************************************** */
void Timer0Init(void)
{
TMOD |= 0x01; // 设置定时器0工作在模式1下
TH0 = 0xDC;
TL0 = 0x00; // 赋初始值
TR0 = 1; // 开定时器0
EA = 1; // 开总中断
ET0 = 1; // 开定时器中断
}
void main(void)
{
Timer0Init();
while(1)
{
PID_Output();
}
}
void Timer0_ISR(void) interrupt 1
{
static uInt16 uiCounter = 0;
TH0 = 0xDC;
TL0 = 0x00;
uiCounter++;
if(100 == uiCounter)
{
g_bPIDRunFlag = 1;
}
}


