LeetCode刷题笔记（8）——分治算法初探

本篇文章总结了LeetCode题目53 最大子序列和中使用的分治算法

53. 最大子序和

题目类型

分治 动态规划

做题总结

分治算法：
实现方式：循环递归

• 在每一层递归上都有三个步骤：

1. 分解：将原问题分解为若干个规模较小、相对独立、与原问题形式相同的子问题
2. 解决：若子问题规模较小且容易解决时，则直接解；否则，递归地解决各子问题
3. 合并：将各子问题的解“合并”为原问题的解

注意事项：

• 边界条件，即求解问题的最小规模的判定

对于本题来讲，分治的情况如下：

 

 

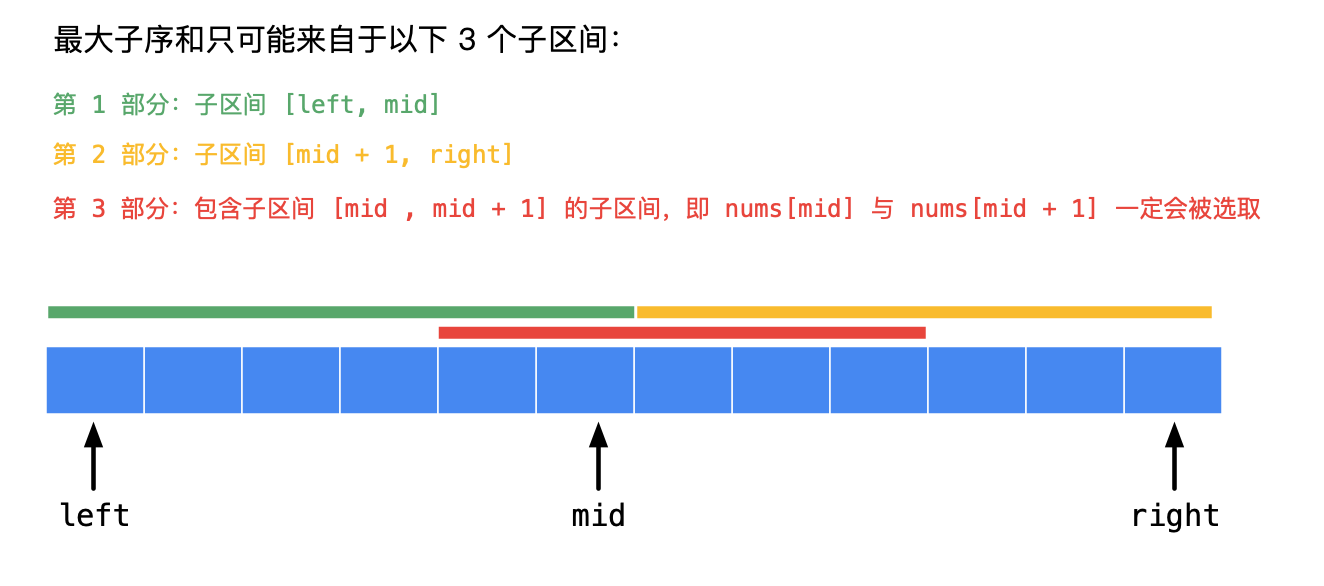
 整个分治过程如下：

 

 

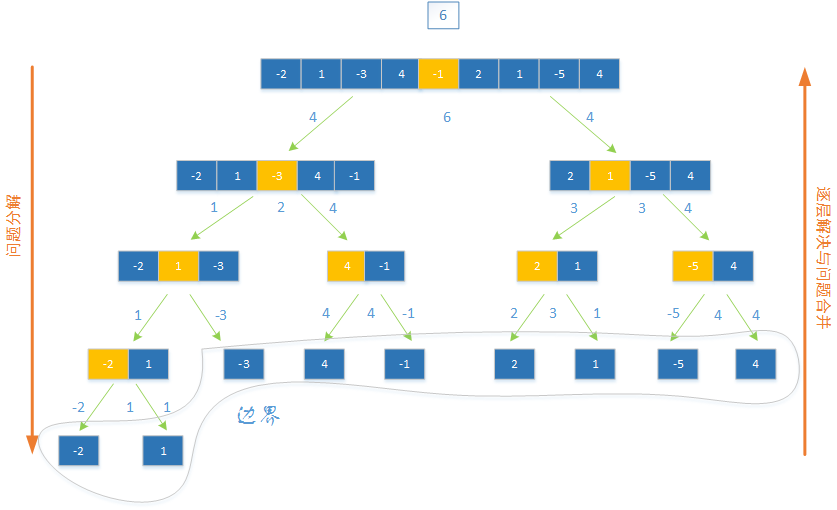
 也可以参照下图：

 

 

 

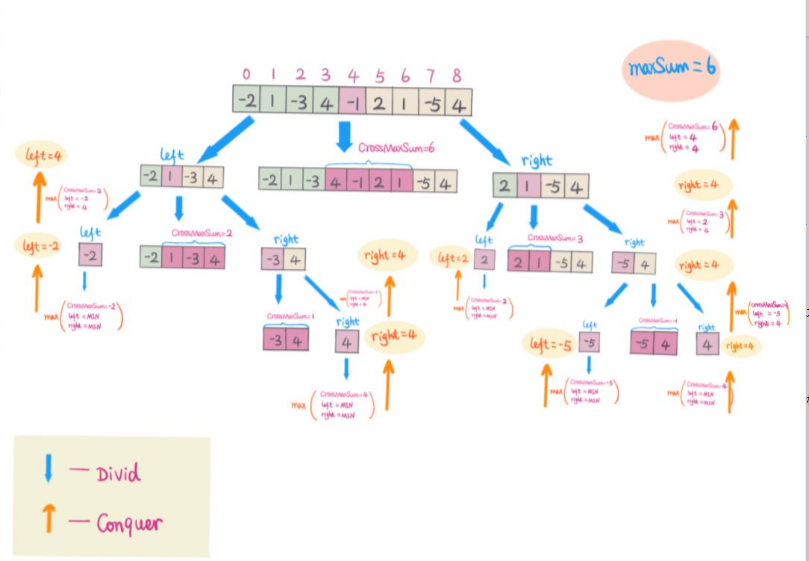
本题的分治解法可参考链接：https://www.bilibili.com/video/BV19t411k7jR?from=search&seid=2021815922201083386

int Max( int val1, int val2 )
{
    return val1 > val2 ? val1 : val2;
}

int maxSubSum( int *nums, int left, int right )
{
    int leftMaxSum, rightMaxSum, crossMaxSum;
    int mid, i;
    //边界条件
    if( left == right )
        return nums[left];

    //分解并递归解决
    mid = (left + right) / 2;
    leftMaxSum = maxSubSum( nums, left, mid );
    rightMaxSum = maxSubSum( nums, mid + 1, right );

    int leftCrossSum = 0, leftCrossSumMax = INT_MIN;
    for( i = mid; i >= left; --i )
    {
        leftCrossSum += nums[i];
        if( leftCrossSum > leftCrossSumMax )
            leftCrossSumMax = leftCrossSum;
    }

    int rightCrossSum = 0, rightCrossSumMax = INT_MIN;
    for( i = mid + 1; i <= right; ++i )
    {
        rightCrossSum += nums[i];
        if( rightCrossSum > rightCrossSumMax )
            rightCrossSumMax = rightCrossSum;
    }
    crossMaxSum = leftCrossSumMax + rightCrossSumMax;

　　//合并
    return Max( Max( leftMaxSum, rightMaxSum ), crossMaxSum );
}

int maxSubArray( int *nums, int numsSize )
{
    return maxSubSum( nums, 0, numsSize - 1 );
}