LeetCode做题笔记(5)——数组中第K大元素——快速选择(快速排序)、优先队列(堆排序)、二分法
本篇文章主要总结了LeetCode经典题 #215数组中第K个最大元素,主要总结了该题的三种解法:快速选择、优先队列、二分法
题目类型
排序
做题总结
二分法
- 本题类似于#378.有序矩阵中第K小的元素,都可以使用二分法的特殊用法——在未排序的数组中进行查找。具体思路为:首先确定数组范围[min, max],令l=min,r=max。mid=r-(r-l)/2,如果大于等于mid的数少于k个,则说明mid取大了,且mid不是第k大的数,因此右边界变为mid-1,于是查找范围变为[l, mid-1];如果大于等于mid的数不少于k个,则说明mid取小了或取得正好,此时mid有可能是第k大的数,因此左边界变为mid,于是查找范围变为[mid, r],当l==r时,二分结束,此时l或r的值即为第k大的数。
- 但本题与#378的不同之处在于#378是查找第k小的数,而本题是查找第k大的数,那么在mid的计算上也就不同。对于查找第k小的数,我们需要在原数组中查找小于等于mid的元素的个数,此时要用mid=l+(r-l)/2,而查找第k大的数时,需要在原数组中查找大于等于mid的元素的个数,此时要用mid=r-(r-l)/2。
- 为什么会有这样的区别呢?问题产生于l与r迭代到二者相邻的时候。设元素组为[1,2,3],k=1,即查找第1大的元素。我们先按照之前常见的mid=l+(r-l)/2的计算方式,首先l=1,r=3,mid=2,大于等于mid的元素个数cnt=2>=k,因此l=mid=2,r=3,mid=2+0=2,原地不动,而正常来讲,mid应该比之前更大一些才对,但由于整数除法的问题,mid无法继续增加。此时如果按照mid=r-(r-l)/2的计算方式,首先l=1,r=3,mid=2,cnt=2>=k,因此l=mid=2,r=3,mid=3-0=3,这时,cnt=1>=k,因此l=mid=3,r=3,l=r已经不满足循环条件,于是退出并返回l(或r)的值,该值即为第k大的数。
- 基于以上经验可以得出结论:当二分法用于查找数组中第k小的数时,mid=l+(r-l)/2;当用于查找第k大的数时,mid=r-(r-l)/2。
- 最后注意一点,这里的二分法不能这样写(类似于常规二分法一样):
这里把cnt等于k的情况单独拿出来直接返回,但这样是错误的,因为数组中可能根本没有值为mid的元素(可能差1也可能差2差3...)。正确的写法是:... if( cnt < k ) { r = mid - 1; cnt = 0; } else if( cnt > k ) { l = mid - 1; cnt = 0; } else { return mid; }
实际上,在二分的过程中,根本无法确定第k大的数是多少,只能等到l=r时。if( cnt < k ) { r = mid - 1; cnt = 0; } else { l = mid; cnt = 0; }
二分法代码如下:int findKthLargest( int *nums, int numsSize, int k ) { int i, min = INT_MAX, max = 0; for( i = 0; i < numsSize; ++i ) { min = nums[i] < min ? nums[i] : min; max = nums[i] > max ? nums[i] : max; } int l = min, r = max, mid, cnt = 0; while( l < r ) { mid = r - (r - l) / 2; for( i = 0; i < numsSize; ++i ) { if( nums[i] >= mid ) ++cnt; } if( cnt < k ) { r = mid - 1; cnt = 0; } else { l = mid; cnt = 0; } } return l; }
快速查找
- 在使用快速查找时,可以将第K大问题转换为第(N+1-K)小问题
- 这里,快速选择的枢轴数pivot取法为三数取中法,没有用取数组左值法,因为可能会达到一个很坏的情况;也没有用随机数法,因为一方面是C的随机数函数还不会用,另一方面是随机数的生成也是很拖性能的。
- 快速选择是由快速排序法稍作改动得来的,即在快排的每一次迭代后,判断枢轴是否就在位置K处,如果是则找到了Kth,因为左边的值都比枢轴小,右边的都比它大;如果枢轴所在位置小于K,则说明Kth在枢轴右边,于是对枢轴右侧进行递归,否则对左边进行递归,直到枢轴的位置为K
- 首先说一下快速排序,快速排序的写法有多种,主要是围绕枢轴的选取方法展开的,以下介绍取边界值法,三数取中法,三数取中加插入排序法。
取边界值法
该方法是最简单的枢轴选取方法,但有一个明显的缺点:如果输入的数组刚好是顺序或逆序的,其时间复杂度会达到O(N)。
void Qsort( int a[], int left, int right )
{
if( left >= right )
return;
int pivot = a[right];
int i = left - 1, j = right;
for( ;; )
{
//left和right作为边界,防止越界
//这里用++i,而不能放在while循环中,因为如果left和right分别指向了2个
//等于pivot的数,则left和right就会死在原地无法前进
//由于i左边的数都是小于pivot的,j右边的数都是大于pivot的,因此
//在ij没触碰边界的情况下,二者退出死循环时,要么i在j右边且紧挨着j,
//要么是ij重合(ij都指向一个等于pivot的数);而i或j触碰边界的情况一般
//为:a[] = 1,2,3,4,0,则j第一次就会触界,实际上i不需要防越界条件,
//因为pivot为a[right],i会首先检查到该条件。如a[] = 1,2,3,4,5时。
//在《数据结构与算法》中就巧妙地设置了防越界条件——三数取中值后,
//将另外两个数分别放到两边。
while( a[++i] < pivot && i < right ){ }
while( a[--j] > pivot && j > left ){ }
if( i < j )
Swap( &a[i], &a[j] );
else
break;
}
Swap( &a[i], &a[right] ); //如果是以a[left]为pivot,则Swap( &a[j], &a[left] );
Qsort( a, left, i - 1 );
Qsort( a , i + 1, right );
}三数取中法
int Median3( int a[], int left, int right )
{
int center = (left + right) / 2;
//对三个数进行排序,最小的放在数组最左边
//最大的放在数组最右边,中值暂时放在mid处
if( a[left] > a[center] )
Swap( &a[left], &a[center] );
if( a[center] > a[right] )
Swap( &a[center], &a[right] );
if( a[left] > a[center] )
Swap( &a[left], &a[center] );
//把中值(枢轴)放到右边倒数第二个位置上
Swap( &a[center], &a[right - 1] );
return a[right - 1];
}
void Qsort( int a[], int left, int right )
{
//当left和right中间只有2个元素时,三数取中
//法无法处理,此时要用特殊处理
if( right - left > 1 )
{
int pivot = Median3( a, left, right );
int i = left, j = right - 1;
for( ;; )
{
//这里不用判断边界条件,借助了三数取中法
//的好处:在数组左右边放置了边界,无需再
//考虑复杂的边界问题
while( a[++i] < pivot ) {}
while( a[--j] > pivot ) {}
if( i < j )
Swap( &a[i], &a[j] );
else
break;
}
//此时i在j右边,因此将pivot放在此处
Swap( &a[i], &a[right - 1] );
//递归地进行排序,直到left和right之间只有2个元素
//这时进入else进行特殊处理,然后退出当前递归,逐
//层返回
Qsort( a, left, i - 1 );
Qsort( a, i + 1, right );
}
else
{
if( a[left] > a[right] )
Swap( &a[left], &a[right] );
}
}三数取中+插入排序
加插入排序一方面解决三数取中时元素少于3个的问题,另一方面时为了解决元素数量较少时快排效率不高的问题。
#define CUTOFF ( 3 )
void InsertionSort( int a[], int n )
{
int j, p;
int tmp;
for( p = 1; p < n; ++p )
{
tmp = a[p];
for( j = p; j > 0; --j )
{
if( a[j - 1] > tmp )
//把大的往后窜直到碰到比它小的,这时就找到了
//插入的位置(前面都比它小,后面都比他大)
a[j] = a[j - 1];
else
break; //前面都是按从小到大排顺序好的
}
a[j] = tmp; //已找到合适位置,执行插入操作
//也可以这样简写for循环:
//for( j = p; j > 0 && a[j - 1] > tmp; --j )
// a[j] = a[j - 1];
//a[j] = tmp;
}
}
void Qsort( int a[], int left, int right )
{
if( left + CUTOFF < right )
{
int pivot = Median3( a, left, right );
int i = left, j = right - 1;
for( ;; )
{
while( a[++i] < pivot ) {}
while( a[--j] > pivot ) {}
if( i < j )
Swap( &a[i], &a[j] );
else
break;
}
Swap( &a[i], &a[right - 1] );
Qsort( a, left, i - 1 );
Qsort( a, i + 1, right );
}
else
InsertionSort( a + left, right - left + 1 );
}快速选择只需修改快速排序的递归部分,这里在三数取中法的基础上修改为了快速选择,代码如下:
void Qselect( int a[], int left, int right, int k )
{
if( right - left > 1 )
{
int pivot = Median3( a, left, right );
int i = left, j = right - 1;
for( ;; )
{
while( a[++i] < pivot ){ }
while( a[--j] > pivot ){ }
if( i < j )
Swap( &a[i], &a[j] );
else
break;
}
Swap( &a[i], &a[right - 1] );
if( k <= i )
Qselect( a, left, i - 1, k );
else if( k > i + 1 )
Qselect( a, i + 1, right, k );
//if k == i + 1, Kth num found, so return directly
//need'nt to write this case
}
else
{
if( a[left] > a[right] )
Swap( &a[left], &a[right] );
}
}小顶堆/优先队列
优先队列实际上是使用堆结构来实现的,堆有很多种,包括二叉堆、d堆、左式堆、斜堆等,首先说一下优先队列的实现,然后再说下堆排序。
- 优先队列大多用二叉堆来实现,二叉堆通过将数组元素与到堆中元素一一映射来实现堆的构建,在二叉堆中,如果将数组元素0作为根节点(堆顶),则一个父节点i的左儿子下标为2i+1,右儿子为2i+2,同理,如果儿子节点为i,则其父节点下标为(i-1)/2;如果以数组元素1作为根节点,则父节点i的左儿子为2i,右儿子为2i+1,儿子节点i的父节点为i/2。
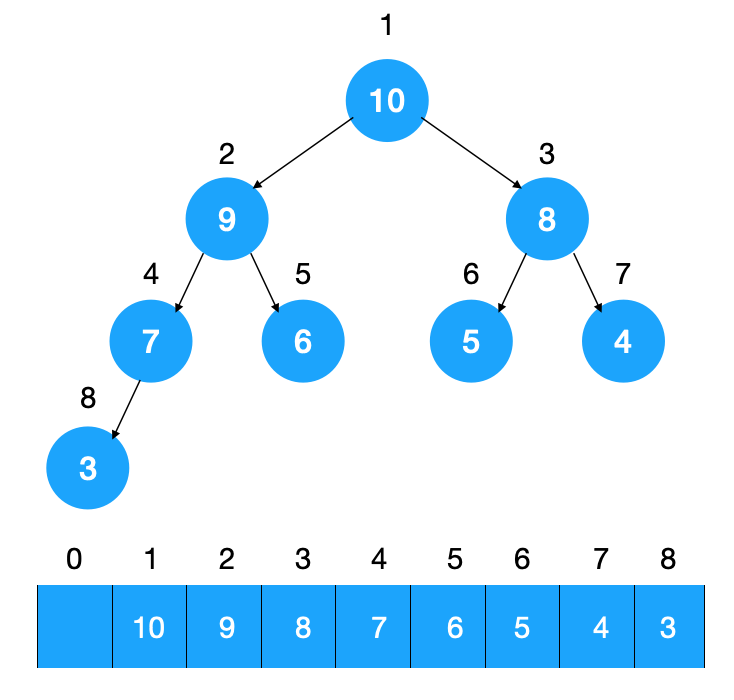
2. 优先队列的实现
struct HeapStruct
{
int Capacity;
int Size;
int *Elements;
};
PriorityQueue Initialize( int MaxElements )
{
PriorityQueue H = malloc( sizeof(struct HeapStruct) );
H->Elements = malloc( (MaxElements + 1) * sizeof(int) );
H->Capacity = MaxElements;
H->Size = 0;
H->Elements[0] = INT_MIN;
return H;
}
/***********************************************************************
*
* 插入新的元素X时,首先要在数组中增加一个空位,
* 然后在堆找到一个合适的位置将其插入,并且要保证
* 堆序性——父节点小于子节点
*
* “上滤”:
* 从空位处开始,如果其父节点比X大,说明X不能放在此处,
* 因此将父节点下沉到该空位,从而将其原位置空出来,即空位“上滤”,
* 再次比较空位的父节点与X的大小关系,如果父节点大则继续“上滤”,
* 如果父节点的值小于X,则找到了正确的位置,于是将X放到空位处,结束。
*
* #对“上滤”更好的解释————插入值X的“上浮”:
* 首先,在堆中增加一个空位,将新值X放到空位处;
* 然后,比较X与其父节点,若父节点大于X(堆序错误),则二者交换位置,
* 于是X“上浮”,继续比较X与其新的父节点,父节点大于X,则继续交换——“上浮”
* ,如果在比较的过程中发现父节点小于X(正常堆序),则说明已经找到了正
* 确的位置,于是退出循环比较过程,整个插入过程结束。
* (以“上浮”来说明整个过程时,提到了X与父节点的交换,但实际上可以真的
* 做交换,也可以假交换——就像如下程序一样,更高效。所谓“假交换”就是只移
* 动父节点,而不真正移动X,每次上浮时都将父节点与X比较而不是与其真正
* 的儿子2*i或2*i+1比较,这样看起来就好像X每次都与父节点交换并“上浮”了
* 一样^>^)
*
* 说明:在初始化函数中将数组位置[0]设为一个非常小的值,用作边界
* 这样在上浮到根节点时,能够保证正确插入。
*
**********************************************************************/void Insert( int X, PriorityQueue H )
{
int i;
for( i = ++H->Size; H->Elements[i / 2] > X; i /= 2 )
H->Elements[i] = H->Elements[i / 2];
H->Elements[i] = X;
/*这样写更好理解:
i = ++H->Size;
for( ;; )
{
if( H->Elements[i / 2] > X )
{
H->Elements[i] = H->Elements[i / 2];
i /= 2;
}
else
{
H->Elements[i] = X;
break;
}
}
*/
}
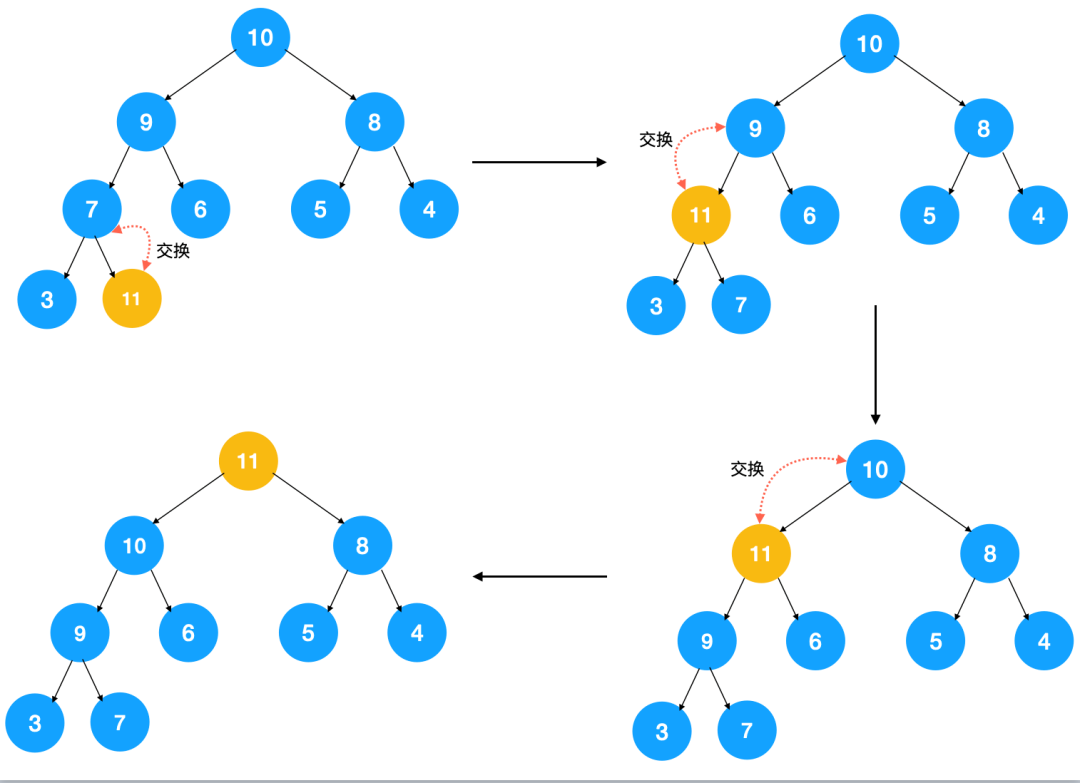
/***********************************************************************
*
* 删除最小元时(这里构造的是小顶堆),最小元就在根节点上,即Elem[1],
* 关键在于删除后如何重新调整堆以保证堆序,首先要将数组删除一个位置,
* 即最后一个元素的位置(删之前先把最后一个元素Last记录下来),然后
* 将元素向根部“挪”,在挪的过程中还得给无家可归的Last物色一个合适的
* 位置,整个过程采用的方法叫做“下滤”。
*
* “下滤”:
* 从根节点处的空位开始,首先寻找两个子节点中较小的(Child),然后将
* Last与Child比较,如果Child更小,则将Child挪到空位,从而使空位下沉,
* 再次找到空位的子节点中较小的值Child,与Last进行比较,如果Child依然
* 更小,则将Child挪到空位,空位继续下沉,如果Last更小,那么说明为Last
* 找到了合适的位置,直接将其安置在空位,整个过程结束。最后还要将删除
* 的堆顶的值返回。
*
* #对下滤更好的解释————“无家可归”元素的“下沉”;
* 首先,明确一点:堆中元素的删除是对堆顶元素的删除,删除后堆顶位置空
* 出,同时堆的大小减1,于是得将堆中最后一个元素的位置删掉,然后将这个
* “无家可归”的元素先记录下来,在重新调整堆序的过程中给他找到合适的位
* 置。具体方法为“下沉”法:
* 首先,将Homeless放到空出的堆顶位置
* 然后,从堆顶开始,比较父节点与较小的儿子,即比较Homeless与较小的儿
* 子,如果小儿子更小,则交换Homeless与小儿子的位置,于是Homeless“下沉”
* ,继续比较下沉后的Homeless与其小儿子,如果小儿子更小则Homeless继续
* “下沉”,如果在下沉的过程中遇到比自己大的小儿子,则说明当前位置合适
* ,于是退出循环比较下沉过程,整个堆序重整过程结束;如果一直下
* 沉到边界后才退出循环比较下沉过程,则说明当前的位置没有子节点了,不
* 存在堆序问题,Homeless直接放在此处就可以了。
*(以“下沉”来说明整个过程时,提到了Homeless与子节点的交换,但实际上可
* 以真的做交换,也可以假交换——就像如下程序一样,更高效)
*
* 说明:这里要注意边界问题,即空位的子节点位置必须在Size范围内,这里
* 在判断边界时,判断的是左子节点(因为空位至少要有一个子节点才行),
* 然后再比较左右子节点的时候,又判断了是否有右节点,判断方法为:
* 判断i * 2 != H->Size,再加上之前的条件——i * 2 <= H->Size,如果判断成
* 立,则说明存在右子节点。
*
**********************************************************************/
int DeletMin( PriorityQueue H )
{
int i, Child;
int MinElement, LastElement;
MinElement = H->Elements[1];
LastElement = H->Elements[H->Size--];
for( i = 1; i * 2 <= H->Size; i = Child )
{
/* find smaller child */
Child = i * 2;
if( Child != H->Size && H->Elements[Child + 1]
< H->Elements[Child] );
++Child;
/* percolate one level */
if( LastElement > H->Elements[Child] )
H->Elements[i] = H->Elements[Child];
else
break;
}
H->Elements[i] = LastElement;
return MinElement;
}
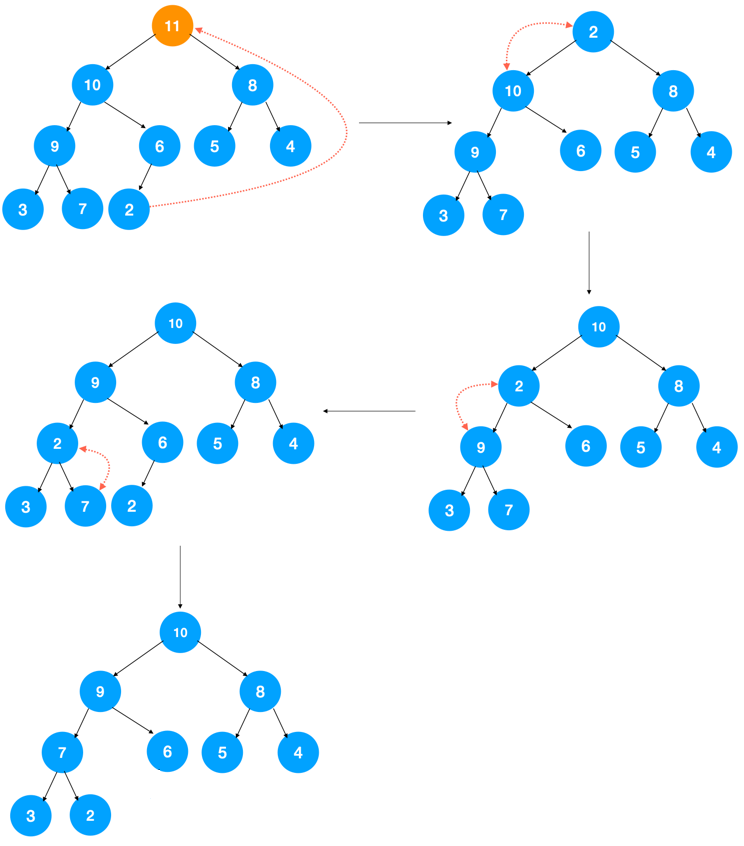
使用优先队列求第K大元素的代码如下:
int findKthLargest( int *nums, int numsSize, int k )
{
PriorityQueue pQueue;
pQueue = PrioQueueInit( numsSize );
int i;
for( i = 0; i < numsSize; ++i )
{
if( pQueue->size == k )
{
if( pQueue->elements[1] < nums[i] )
{
PrioQueueDelete( pQueue );
PrioQueueInsert( pQueue, nums[i] );
}
}
else
{
PrioQueueInsert( pQueue, nums[i] );
}
}
return pQueue->elements[1];
}3.堆排序
/* 取左儿子(堆顶放在数组[0]处) */
#define LeftChild( i ) ( 2 * ( i ) + 1 )
/*******************************************************************
*
* PercDown对父节点i以下的子堆进行堆序整理,操作对象为数组,该程
* 序中默认堆顶在数组[0]位置上,而不像二叉堆结构实现优先队列时将
* 数组[1]位置作为堆顶。这里维护的是一个大顶堆,这适用于从小到大
* 的排序顺序。整个过程与优先队列插入时的下滤过程一样,这里也是
* 用了“假交换”。
*
******************************************************************/
void PercDown( int A[], int i, int N )
{
int Child;
int Tmp;
for( Tmp = A[i]; LeftChild( i ) < N; i = Child )
{
Child = LeftChild( i );
if( Child != N - 1 && A[Child + 1] > A[Child] )
++Child;
if( Tmp < A[Child] )
A[i] = A[Child];
else
break;
}
A[i] = Tmp;
}
/*******************************************************************
*
* 首先将给定数组堆化,这里用下滤函数PercDown从最后一个父节点开
* 始进行堆序整理,直到根节点,整个过程完成后便得到一个大顶堆;
* 然后通过Swap模拟将堆顶元素删除,最后一个元素放到堆顶,并将空
* 出来的地方用来存放删除的堆顶元素,这样就实现了在原数组上排序,
* 而不需要额外的数组空间临时存储被删除的堆顶元素(最后再将其拷
* 回原数组),最后将放在堆顶的最后一个元素进行“下沉”,以重新整
* 理堆序。注意每次堆的大小都会减1,当循环结束后,元素组便成为了
* 一个有序数组(从小到大)。
*
******************************************************************/
void HeapSort( int A[], int N )
{
int i;
for( i = N / 2; i >= 0; --i ) //对数组A建堆
PercDown( A, i, N );
for( i = N - 1; i > 0; --i )
{
Swap( &A[0], &A[i] ); //通过删除
PercDown( A, 0, i );
}
}
}
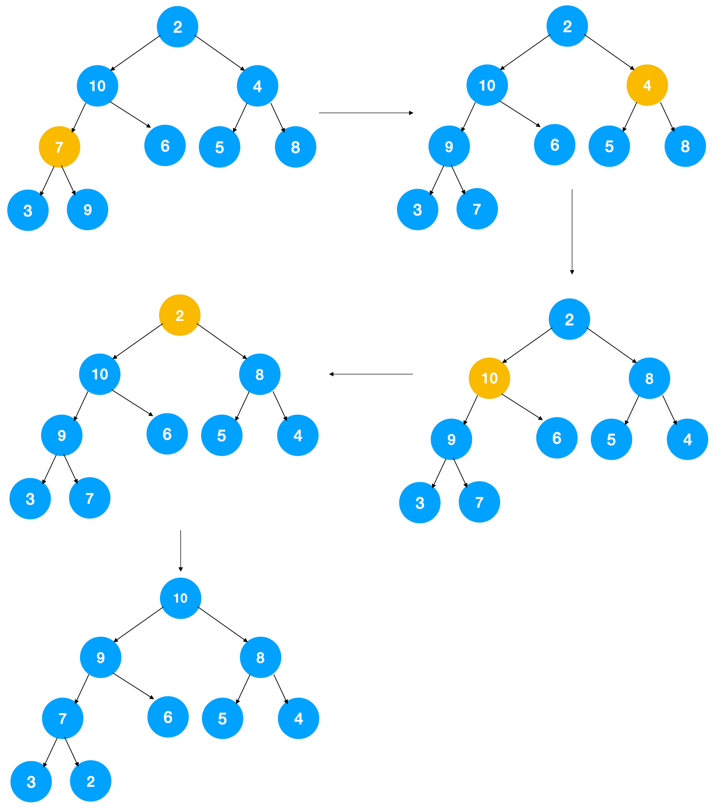
建堆及排序过程如下图所示:
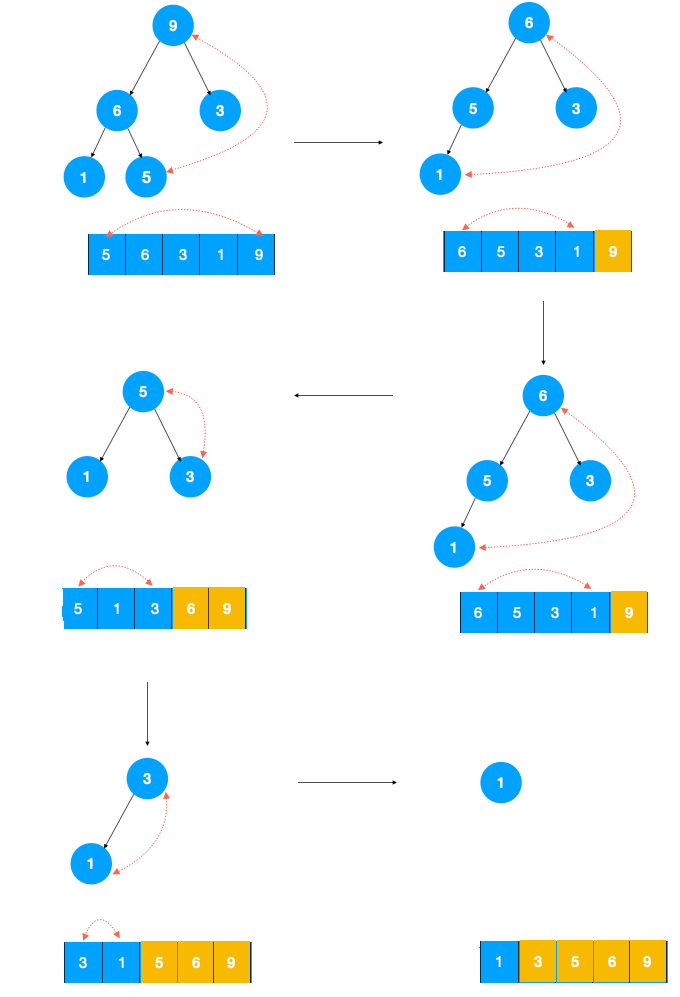
最后,关于逗号运算符:如果if下有多条语句,但又不想加花括号怎么办?——可以用,分割语句:if( a > b ) int tmp = a, a = b, b = tmp;,实际上,for( int i = 1, j = 2; ; i++, j++)也是用了逗号运算符
注:以上图片来源于微芯公众号:五分钟学算法
