CMOS光电转换特性
1. 量子效率和响应率 -PHOTOCONVERSION CHARACTERISTICS
总量子效率(Overall quantum efficiency, QE) 指入射光子转成像素电荷的效率,由下式给出:
式中 , \(N_{sig}(\lambda)\) 是每个像素产生的信号电荷, \(N_{ph}(\lambda)\) 是每个像素的入射光子。如前所述,入射光子有一部分被光电二极管的上部结构反射或者吸收了。微型透镜结构决定了有效填充因子 \(FF\) , 光电二极管结构(从表面到衬底)决定了电荷收集系数。因此,式1可以被表达为
式中, \(T(\lambda)\) 是探测器以上结构的光线透射比, \(FF\) 是有效 , \(\eta(\lambda)\) 是光电二极管的电荷收集效率。 \(N_{sig}(\lambda)\) 和 \(N_{ph}(\lambda)\) 由下式表示 :
式中 \(I_{ph}\) 是光电流 photocurrent,单位为 \(A/cm^2\) ; \(A_{pix}\) 是像素面积,单位为 \(cm^2\) ; \(q\) 是电子电荷量 electron charge ; \(P\) 是输入光功率 optical input power ,单为为 \(W/cm^2\) ; \(t_{INT}\) 是积分时间。
响应率 Responsivity: \(R(\lambda)\) 定义为光电流与光输入功率的比例,由下式给出:
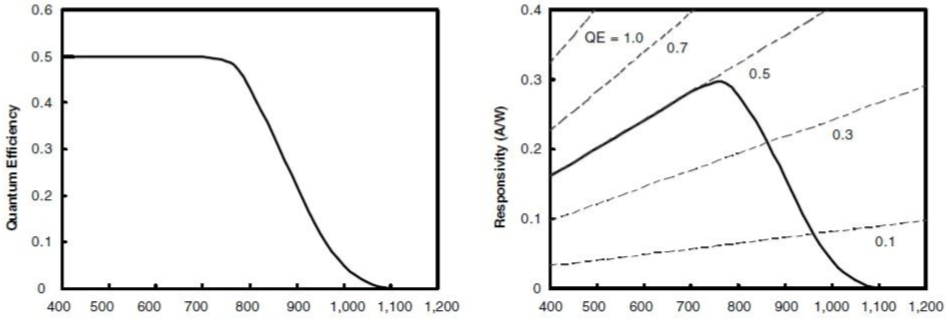
参考上式 5,则光谱响应可以用两种方式表示:响应率 或 量子效率 。为了突出两种表示方式的不同, 我们假设有一个虚拟图像传感器,它在 400~700nm 的波长范围内 QE 值恒为 0.5,其光谱响应如图 1 所示。我们经常使用 相对响应 the relative response ,即将响应值相对它的峰值进行归一化。将彩色滤光器的响应值color filter response(见图像传感器图一)和图像传感器的响应值 image sensor's response 相乘,可以得到整体的颜色响应。
2. 光电转换特性机理 - MECHANICS OF PHOTOCONVERSION CHARACTERISTICS
光电转换特性(photoconversion)表示了输出电压和曝光之间的关系。在数码相机领域,使用标准光源时, 曝光通常以勒克斯秒(lux-seconds)为单位。估计来自标准光源的入射光子数量的过程多少有些复杂, 光电转换的参数将用单色光为例进行说明。在单色光条件下,人射光每单位能量包含的光子数目很容易求出,光电转换的参数细节也容易分析。参考文献2 提供了估算标准光源中的人射光子数量的方法。
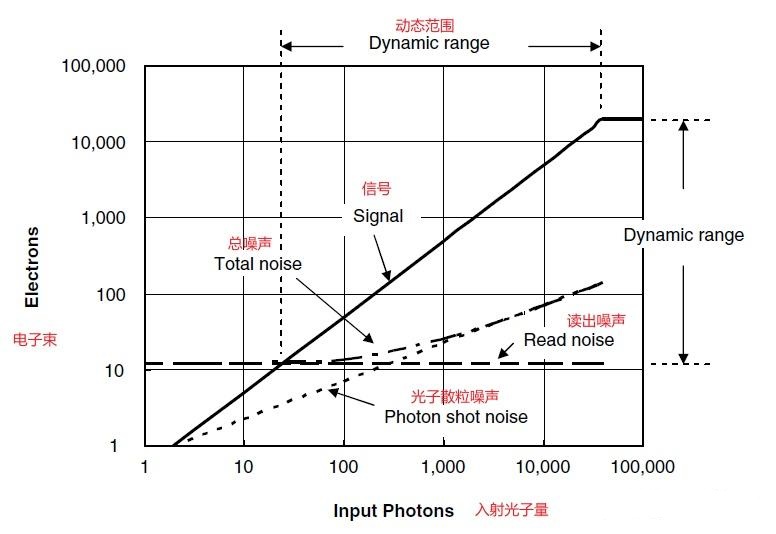
图2 是光电转换参数的一个例子, 展示了信号 Signal、光子散粒噪声 Photon shot noise 和读出噪声(本底噪声) read nosie 与 入射光子量 incident photons 的函数关系。为了做出图2,我们假设了一个虚拟的图像传感器,它的像素尺寸 \(A_{pix}\) 为 \(25 \mu m^2\) , \(C.G(Conversion Gain)\) 为 \(40\mu V/e^-\) , 满阱容量 \(FWC\) 为 \(N_{sat}=20 000\) 个电子, 本底噪声 \(n_{read}=12\) 个电子, 探测器的 \(QE=0.5\) 。该图中未包含暗电流散粒噪声 Dark current shot noise 。
2.1 动态范围和信噪比 - Dynamic Range and Signal-to-Noise Ratio
动态范围(Dynamic range, DR ) 定义为 满阱容量full-well capacity 与 本底噪声the noise floor 之间的比值。信噪比(Signal-to-noise ratio, SNR)是给定输入电压下信号与噪声的比值。它们分别如下式所示:
在图 2 的例子中, DR 的计算方法为: \(20\cdot log(20000/12)=64.4dB\) 。在 SNR 表达式中, 噪声 \(n\) 是在信号电平为 \(N_{sig}\) 时的 总暂态噪声total temporal noise。在 总噪声中以读出噪声为主 , SNR 由下式表示:
在光子散粒噪声占主要部分时, 采用光子散粒噪声估计转换增益如sensor nosie式23,可以表示为
图 3 展示了 SNR 与入射光子数的函数关系。由式 9 可知,最大 SNR 仅由满阱容量决定,见下式:

🌻 测量图像信噪比SNR参数:
使用 “Image J” 来测试图片的信噪比,暗电流噪声会随着时间而累积,因此在需要长时间曝光的实验(如WB实验)中,暗电流会产生较大的影响。CCD制冷是降低暗电流的手段之一,而我们真正应该关心的并非CCD的制冷温度而是暗电流的大小,因此需要保证在较短的曝光时间内测量图像的SNR信噪比:
- 计算背景区域平均灰度值(Mean)和背景噪声标准差(StdDev),此区域所采集到的灰度值来自相机的噪声
- 计算目标区域的平均灰度值(Mean)
- 信噪比的计算:信噪比为信号与噪声的比值,在计算信噪比时,我们先用目标区域的信号减去背景的信号,随后除以背景区域噪声的标准差:
SNR=(目标区域信号-背景噪声)/噪声标准差
🚀 实验如下:
2.2 量子效率的估算 - Estimation of Quantum Efficiency
量子效率易从图 2 中得出,在本例中为 0.5。同时,也可以通过 SNR 曲线中 (如图 2 所示 ) 散粒噪声为主的部分估算量子效率,如下式:
式中 , \(S/N\) 为 \(N_{sig}/n_{photo}\) 然后,入射光子的数量 (见图 2 的横轴) 需要转换为曝光量,信号电子的数量(见图 2 的纵轴)需要转换为输出电压 (在本例中, 是检测点电压或输入参考电压)。对于单色光来说,人射光子的数量由下式给出:
2.3 转换增益的估算 - Estimation of Conversion Gain
将图像传感器的信号电荷转换为信号电压的过程,按以下关系进行:
式中, \(C.G\) 是转换增益(见式 14 )。采用光子散粒噪声估计转换增益如sensor nosie式23:
式 13 和式 15 导出以下关系式 :
因此,转换增益可以由 \(V_{sig}\) 与 \(v_{photo}^2\) 的关系图的斜率获得。在该估算方法中, 光子散粒 噪声被视为提供有用信息的“信号”, 因而可以得到曝光量与输出电压的关系,如图 4 所示。
2.4 满阱容量的估算 - Estimation of Full-Well Capacity
式 10 表明, 满阱容量可以通过用实验测量最大信噪比来获得:
同样地,在图 4 中,因为信号线与光子散粒噪声的交点发生在 \(N_{sig}=1\) 处(此处信号电压等于转换增益)满阱容量(或者饱和电荷) \(N_{sat}\) 可以从图中估出。
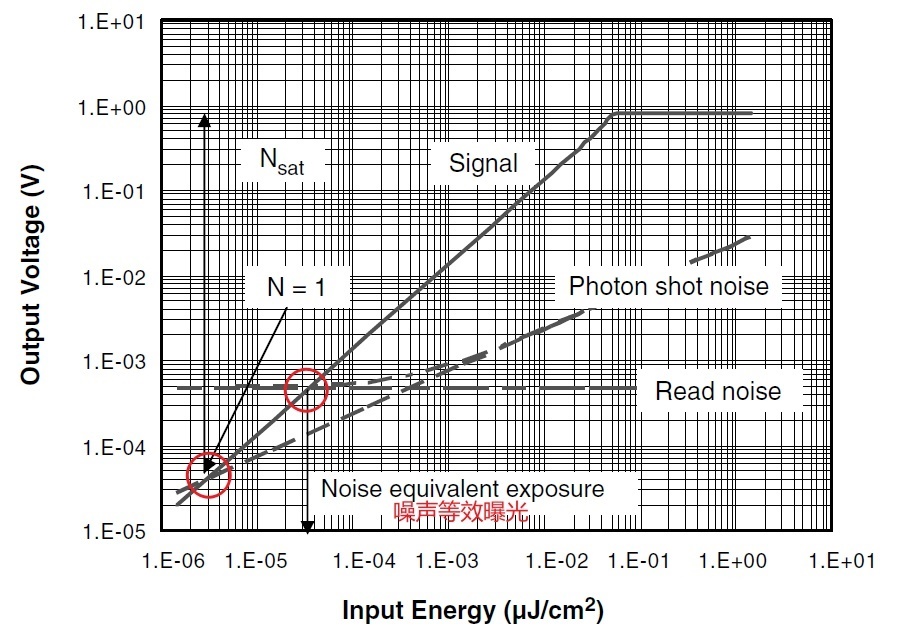
上图表示在单色光波长为550nm处曝光量 vs 电荷检测点的信号电压情况,结果如下:
- \(QE=0.5\)
- \(A_{pix}=25\mu m^2\)
- \(C.G=40\mu V/e^-\)
- \(N_{sat}=20000e^-\)
- \(n_{read}=12e^-\)
2.5 噪声等效曝光度 - Noise Equivalent Exposure
噪声等效曝光度(Noise equivalent exposure)可以定义为信号电平等于读出噪声电平时,也就是信噪比等于 1 时的曝光量。
实际上,入射光子和信号电荷之间的关系的推导须反向进行,即从获取图像传感器曝光量和输出信号的关系开始。采用该种方法的前提是假设光电转换特性是线性的,而且没有失调电压。若非如此(例如由暗电流会引起非线性和失调),则应在修正之后再采用该方法获得转换增益。
在实际器件中,信噪比 (包括FPN固定定模式噪声) 实际限制着真正的成像信噪比,因为一次拍照同时包含这两个来源。另外, PRNU 限制了最大信噪比,因为 PRNU 的增长 与 散粒噪声的增长 分别正比于 信号电子数 及 其平方根。在 PRNU 线性度大约为 \(1\%\) 的条件下, 不管满阱容量有多大, 最大 SNR(包括 PRNU)永远不可能超过 40dB。
2.6 线性度 - Linearity
光电转换固然是一个线性过程。然而,从电子到信号电荷的转换 (如电荷收集效率) 和 信号电荷到输出电压的转换则可能是非线性的过程。
在 CCD 图像传感器中, 非线性可能源于随电压变化的 浮置扩散型电容floating diffusion 以及 输出放大器output amplifier 的非线性。然而, 这些非线性的影响通常很小, 因为相比于拥有高偏置电压(约 15V)的输出放大器,非线性来源部分的工作电压范围非常有限( <1V)。在 IT CCD 中,最值得注意的非线性出现在饱和电平附近, 因为像素中有垂直溢出漏极结构(vertical overflow drain structure)。该非线性来源于从光电二极管电荷储存区域到垂直溢出漏极的电子转移。
2.7 串扰 - Crosstalk
串扰有两种成分:光学optical串扰和电学electrical.串扰。光学串扰成分来源于漫射光或对角度敏感的片上微透镜阵列,如 像素中的光电探测器图 2 所示。不考虑电学串扰成分的前提下,波长较长的光发生光电转换生成信号电荷的区域较深,可能会扩散到相邻的像素。减少该类电荷扩散的方法,包括:
在保持表面对红光光谱响应率的条件下,使有效光电转换深度变浅。例如,使用正向偏置 n 型衬底 (见 像素中的光电探测器图 4b )。
在像素问加入隔离区。例如,对于 CMOS 图像传感器可以采用更高渗杂度的 p 型隔绝区包围光电二极管区域。
正如 像素中的光电探测器图 所描述的,对于小型像素来说,通常会制作片上微型透镜以增加灵敏度。微型透镜能将人射光线汇聚到光电二极管区域的中心上,因此也能减少串扰。
3 灵敏度和信噪比 - SENSITIVITY AND SNR
灵敏度, 作为图像传感器中最重要的性能指标, 通常被定义为输出信号变化与输入光线变化的比值,常用单位有伏特每勒克斯秒volts per lux-second、电子每勒克斯秒electrons per lux-second、位每勒克斯秒bits per lux-second等。然而,这个定义并没有明示“图像传感器能够捕获并仍能产生输出图像的最暗场景是什么?”这一问题。为了解决这个问题,我们需要知道图像传感器的“灵敏度”(输出变化与输人变化之比)和它的噪声水平。在非常低的光线水平下, 噪声等效曝光度包括了上述两个因素的影响。当考虑从暗到亮的整个光照范围时,信噪比是对图像传感器真正“灵敏度”的衡量标准。
3.1 如何提高信噪比 - HOW TO INCREASE SIGNAL-TO-NOISE RATIO
显然, 信噪比可以通过加强信号和减小噪声来提高。为了加强信号,必须提高量子效率。由式1表示,其分解后得式2,可知需要提高下列项:
- 光的透射比 \(T(\lambda)\) :减少颜色滤光片吸收; 减小 SiOz/Si 接触面的反射率。
- APS填充因子 \(FF\) :减小像素中的非探测区域;优化微型透镜结构。
- 电荷收集效率 \(\eta(\lambda)\) : 由优化微探测器结构并避免像素间串扰。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号