基础物理概念
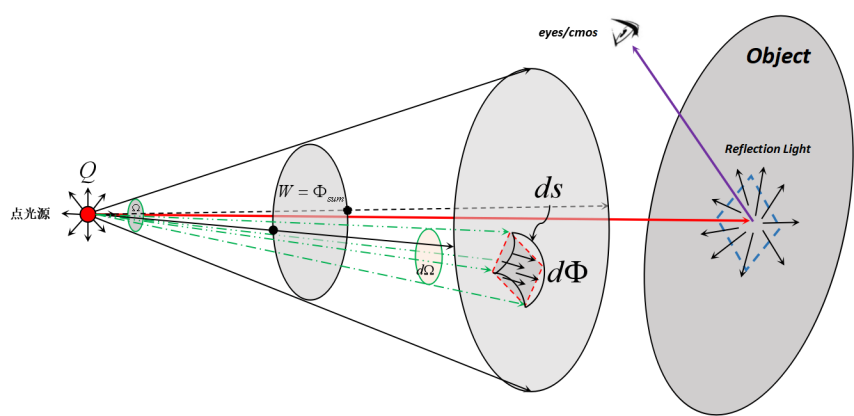
🌻 Tips: 立体角的规定为当前球面表面积与球体半径平方的比值，因此整个球面对应的立体角为 \(\Omega=S_{Sphere}/R^2=4\pi R^2/R^2=4\pi\)，故此立体角公式为：\(d\Omega=dS/r^2\)
一、辐射学
1. 辐射通量
辐射通量又称辐射功率，指单位时间内通过某一截面的辐射能，是以辐射形式发射、传播或接收的功率，单位为 \(W\)（瓦），即 \(1W=J/s\)（焦耳每秒）。它也是辐射能随时间的变化率 \(\Phi=dQ/dt\) 。测量辐射通量的方法一般是由直流电置换辐射通量的等价置换原理进行的。
2. 辐射照度
辐射照度又称辐照度，是受照面单位面积上的辐射通量，单位：瓦每平方米（ \(W/m^2\) ）；辐射照度表征了受辐射能照射的表面上，单位面积单位时间内接收的辐射能的多少，即受照面上的辐射通量密度。计算公式如下：
\(I\) 表示辐射照度，\(\Phi\) 表示光通量，\(S\) 表示面积。
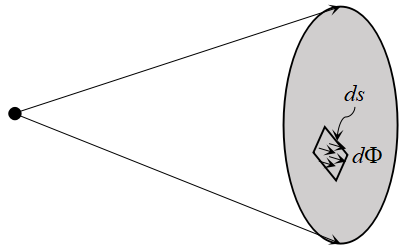
3. 辐射强度
点辐射源在某方向上单位立体角内传送的辐射通量，记作 \(I_e\) ，即 \(I_e=d\Phi_e/dΩ\) ，式中 \(d\Phi_e\) 是 \(d\Omega\) 立体角元内的辐射通量。 辐射强度的 \(I_e\) 单位为 瓦/球面度 。多数辐射源的辐射强度正比于该方向与表面法线之间夹角的余弦，这样的辐射源称为余弦辐射体或朗伯辐射体。
4. 辐射亮度
辐射亮度简称辐亮度，辐射亮度表示面辐射源上某点在一定方向上的辐射强弱的物理量。指面辐射源在单位时间内通过垂直面元法线方向 \(\vec n\) 上单位面积、单位立体角上辐射出的能量，即辐射源在单位投影面积上、单位立体角内的辐射通量。
辐射亮度的 \(SI\) 单位为 瓦/(球面度x米^2) 。面辐射源的辐射亮度 \(L_e\) ：辐射源在某一方向的单位投影面积在单位立体角内的辐射通量，称为辐射亮度 (Radiance) \(L_e\)。\(L_e=dI_e/(dS \cdot cos\theta)\)； \(I_e\) 为辐射强度，\(\theta\) 为给定方向和辐射源面元法线间的夹角。单位是 \(W/(sr\cdot m^2)\)。
二、光度量学
1. 光通量概念
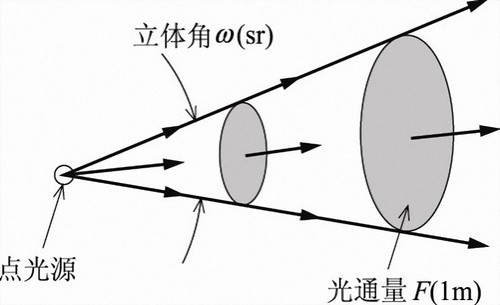
光通量 （luminous flux） 指人眼所能感觉到的辐射功率，单位为 \(lm\) (流明)，它等于单位时间内某一波段的 辐射能量 和该波段的 相对视见率 的 乘积 。由于人眼对不同波长光的相对视见率不同，所以不同波长光的辐射功率相等时，其光通量并不相等；光通量与辐射通量的关系如下：
式中 \(K_m\) 为光谱光视效能的最大值，等于 \(683lm/W\) ; \(V(\lambda)\) 为国际照明委员会 (CIE) 规定的标准光谱光视效率函数; \(\phi_{eλ}\) 为辐射通量的光谱密集度。
\(1lm\) 等于由一个具有 \(1cd\) (坎德拉) 均匀的发光强度的点光源在 \(1sr\) (球面度)单位立体角内发射的光通量，即 \(1 lm=1 cd·sr\) 。一只 \(40W\) 的普通白炽灯的标称光通量为 \(360lm\) ，\(40 W\) 日光色荧光灯的标称光通量为\(2100 lm\) ，而 \(400 W\) 标准型高压钠灯的光通量可达 \(48000 lm\) 。
2. 发光强度概念
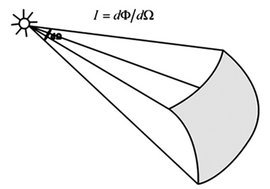
发光强度 (Luminous intensity) 是基于人眼模型定义的，该物理量考虑了人眼的相对视见效率，在光度学中简称光强或光度。用于表示光源给定方向上单位立体角内光通量的物理量，国际单位为坎德拉，符号：cd ，以前又称烛光、支光。其物理表达式如下：
物理意义： 发光体在给定方向上的发光强度是该发光体在该方向的立体角元 \(d\Omega\) 内传输的光通量 \(d\Phi\) 除以该立体角元所得之商，即单位立体角的光通量。
📓 Example: 发光强度为1烛光的点光源，在单位立体角（1球面度）内发出的光通量为“1流明”?
考虑到1烛光时间上为光强度单位，1烛光=\(1cd\)，据此计算光通量如下：
3. 光照强度(照度)概念
光照强度是指单位面积上所接受可见光的能量，简称照度，单位勒克斯 （Lux或lx） 。为物理术语，用于指示光照的强弱和物体表面积被照明程度的量。其物理表达式如下：
\(1 lux=1 lm/m^2\) : 被光均匀照射的物体，在1平方米面积上所得的光通量是1流明时，它的照度是1勒克斯；流明是光通量的单位。
4. 光亮度
光亮度 (luminance) 又称发光率，是指一个表面的明亮程度，以 \(L\) 表示， 即光源在垂直其光传输方向的平面上的正投影单位表面积单位立体角内发出的光通量。
物理意义： \(ds'=ds·cosθ\) ，面元沿这个方向的发光强度为 \(dI\) ，则光源在该方向上的光亮度为 \(L=dI/(cosθ \cdot ds)\) ；若面元沿这个方向上立体角元 \(d\Omega\) 内发出的光通量为 \(d\Phi\) ，因此 \(dI=d\Phi/d\Omega\) ，光亮度又可写为 \(L=d\Phi/(d\Omega \cdot ds \cdot cosθ)\)；在国际单位制中，光亮度的单位是 坎德拉/平方米 \((cd/m^2)\)，又称尼特 nit 。
三、色度学
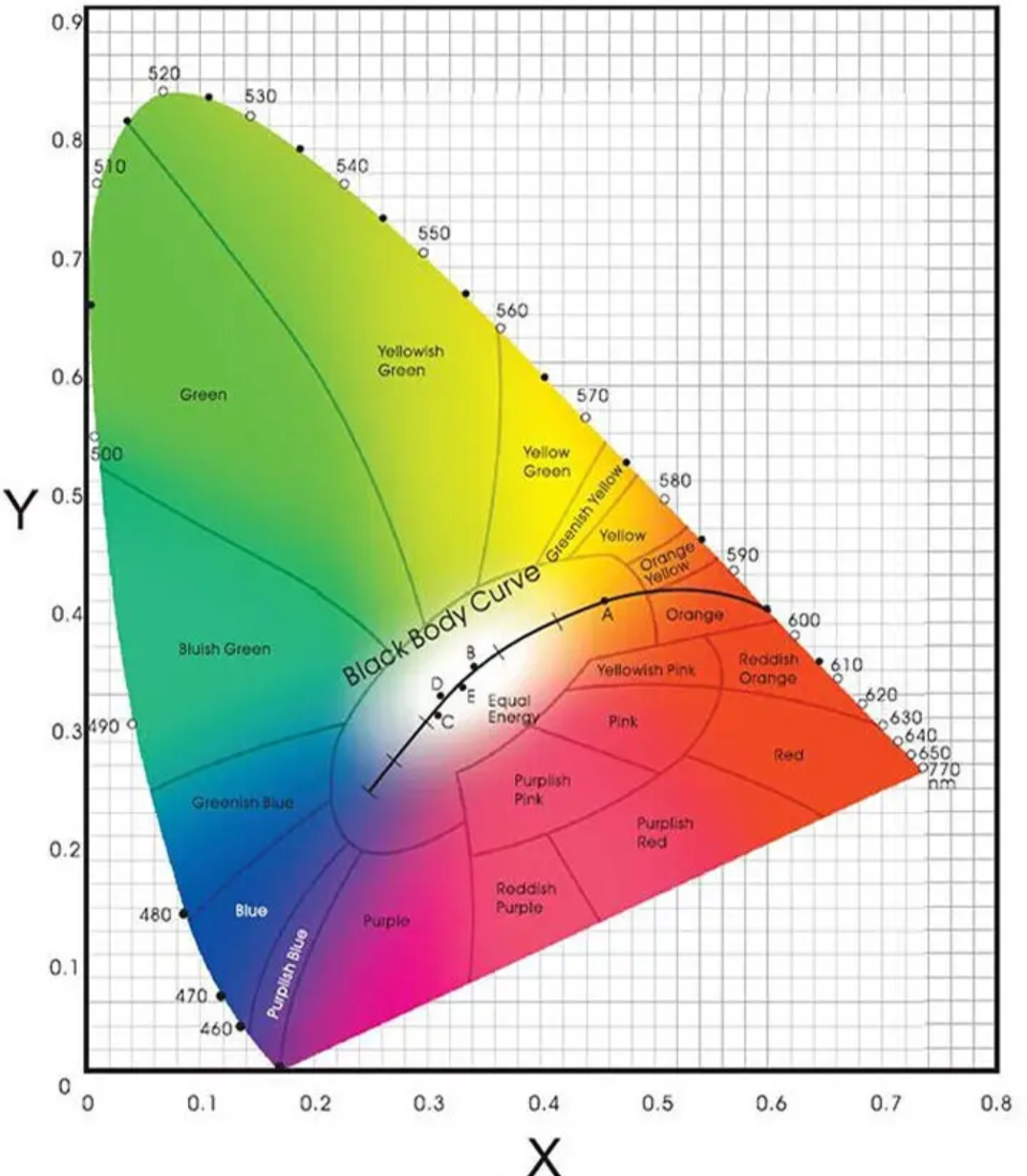
CIE 1931色度图是用标称值表示的CIE色度图，x表示红色分量，y表示绿色分量。E点代表白光，它的坐标为(0.33，0.33);环绕在颜色空间边沿的颜色是光谱色，边界代表光谱色的最大饱和度，边界上的数字表示光谱色的波长，其轮廓包含所有的感知色调。所有单色光都位于舌形曲线上，这条曲线就是单色轨迹，曲线旁标注的数字是单色(或称光谱色)光的波长值;自然界中各种实际颜色都位于这条闭合曲线内;RGB系统中选用的物理三基色在色度图的舌形曲线上。
