矩阵 — 点乘与叉乘

点乘

基本概念

• 简而言之就是矩阵各对应元素相乘。
• 需满足乘数矩阵和被乘数矩阵的行向量或列向量相等，或两者同时相等。

数学公式

S1 矩阵尺寸不完全相同

\[C=AB= \begin{bmatrix} a_{11} \\ a_{21} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{bmatrix}= \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{11}b_{13} \\ a_{21}b_{21} & a_{21}b_{22} & a_{21}b_{23} \end{bmatrix} \]

S2 矩阵尺寸完全相同

\[C=AB= \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{bmatrix}= \begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & a_{13}b_{13} \\ a_{21}b_{21} & a_{22}b_{22} & a_{23}b_{23} \end{bmatrix} \]

Python测试代码

numpy 库中可使用运算符 * 或 multiply 函数计算。

A = np.array([[1],[2]])
B = np.array([[1,2,4],[1,4,5]])
C = np.array([[1,2,3],[4,5,6]])

X = A*B
array([[ 1,  2,  4],
       [ 2,  8, 10]])

X == np.multiply(A,B)
array([[ True,  True,  True],
       [ True,  True,  True]])

Y = B*C
array([[ 1,  4, 12],
       [ 4, 20, 30]])
Y == np.multiply(B,C)
array([[ True,  True,  True],
       [ True,  True,  True]])

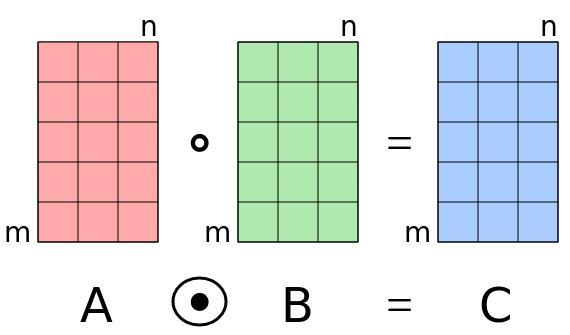
需要点出的是：
当矩阵A和矩阵B的维度相同时，矩阵点乘即为哈达玛积（Hadamard Product），如下图所示：

叉乘

基本概念

• 就是我们熟知的矩阵乘法。
• 中间相同留两边。

S1 示例

\[C=A \times B= \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\times \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{bmatrix}= \begin{bmatrix} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} & a_{11}b_{13}+a_{12}b_{23} \\ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} & a_{21}b_{11}+a_{22}b_{23} \end{bmatrix} \]

Python测试代码

numpy 库中可使用运算符 @ 或 dot 函数计算。

A = np.array([[1,2],[3,4],[1,5]])
B = np.array([[1,2],[2,1]])

A@B
array([[ 5,  4],
       [11, 10],
       [11,  7]])

A@B  == np.dot(A,B)
array([[ True,  True],
       [ True,  True],
       [ True,  True]])

Reference

矩阵点乘/叉乘