Hiho----有向图欧拉回路

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho破解了一道又一道难题，终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。

宝箱被一种奇怪的机关锁住：

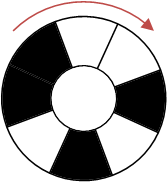
这个机关是一个圆环，一共有2^N个区域，每个区域都可以改变颜色，在黑白两种颜色之间切换。

小Ho控制主角在周围探索了一下，果然又发现了一个纸片：

机关黑色的部分表示为1，白色的部分表示为0，逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布，使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次，终究没有办法打开，只得在此写下机关破解之法。
	——By 无名的冒险者
	

小Ho：这什么意思啊？

小Hi：我给你举个例子，假如N=3，我们通过顺时针转动，可以使得正下方的3个区域表示为：

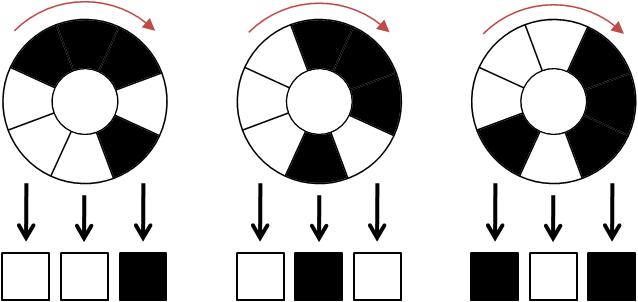
因为黑色表示为1，白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)

每转动一个区域，可以得到一个新的数字。一共可以转动2^N次，也就是2^N个数字。我们要调整黑白区域的位置，使得这2^N个数字恰好是0~2^N-1

小Ho：我懂了。若N=2，则将环上的黑白色块调整为"黑黑白白"，对应了"1100"。依次是"11","10","00","01"四个数字，正好是0~3。那么这个"黑黑白白"就可以打开机关了咯？

小Hi：我想应该是的。

小Ho：好像不是很难的样子，我来试试！

提示：有向图欧拉回路

输入

第1行：1个正整数，N。1≤N≤15

输出

第1行：1个长度为2^N的01串，表示一种符合要求的分布方案

样例输入

3

样例输出

00010111

代码： 经过Hiho在线测试，符合题目要求。

import java.util.ArrayList;
import java.util.Scanner;


public class Main {

    ArrayList result = new ArrayList();
        public static void main(String[] argv){
            
            Scanner in = new Scanner(System.in);
            int N = in.nextInt();
            int m = (int)Math.pow(2, N-1);
            int n = (int)Math.pow(2, N);
            //System.out.println(m);
            int Move =32-N+1;

            ArrayList<Integer>[] s = new ArrayList[m];
            for(int i=0; i<m; i++){
                s[i] = new ArrayList<Integer>();
            }
            
            for(int j=0; j<m; j++){
            
                    s[j].add((2*j)%m);
                    s[j].add((2*j+1)%m);
                
                
                //System.out.println("  "+j+"  "+s[j].get(0)+"  "+s[j].get(1));
            }
            in.close();
            Main Test = new Main();
            Test.DNF(s, 0);
            //System.out.print(0+" "+0);
            /*
            for(int i=0;i<Test.result.size(); i++){
                if(i>0)
                    System.out.print(" ");
                System.out.print(" "+Test.result.get(i));
            }
            */
            System.out.println("");
            for(int i=0;i<n; i++){
                
                System.out.print((int)Test.result.get(i)%2);
            }
        }
        
public void DNF(ArrayList[] s, int start){
            
            while(true){
                
                   if(s[start].size()>0){                       
                       int temp = (Integer)s[start].get(0);
                       s[start].remove(0);
                       //s[temp].remove((Integer)start);
                       DNF(s, temp);                
                   }    
                   else 
                       break;
            }
            result.add(start);
            //System.out.print(start);
            
        }
        
}