快速多项式乘法
快速多项式乘法
FFT
多项式的表示方法
系数表示法
\(A(x)=\sum_{i=0}^{n} a_{i} * x^{i}\)表示为\({\{a_0,a_1,...a_n}\}\)
点值表示法
\(A(x)=\sum_{i=0}^{n} a_{i} * x^{i}\)表示为\({\{x_0,y_0,x_1,y_1...x_n,y_n}\}\)
优化多项式乘法的思路
如果用系数表示法进行多项式乘法,时间复杂度显然是\(O(n^2)\)的。
对于点值表示法,如果两个多项式用的是同一组x坐标,那么只要将对应的y坐标相乘即可,时间复杂度是\(O(n)\)的。
但是一般用的多项式是系数表示法,而朴素的系数表示法转点值表示法是\(O(n^2)\),点值表示法转系数表示法(高斯消元法)甚至达到了\(O(n^3)\),想通过点值表示法进行快速多项式乘法则必须解决这两个瓶颈。
单位根
下文中,默认 \(n\) 为2的正整数次幂
在复平面上,以原点为圆心, 1为半径作圆, 所得的圆叫单位圆。以圆点为起点, 圆的n等分点为终点, 做\(n\)个向量, 设幅角为正且最小 的向量对应的复数为 \(\omega_{n},\) 称为\(n\)次单位根。
根据复数乘法的运算法则, 其余 \(n-1\) 个复数为 \(\omega_{n}^{2}, \omega_{n}^{3}, \ldots, \omega_{n}^{n}\)
注意 \(\omega_{n}^{0}=\omega_{n}^{n}=1\) (对应复平面上以 \(x\) 轴为正方向的向量)
那么如何计算它们的值呢? 这个问题可以由欧拉公式解决
下文默认点值表示法选定的x为\(\omega_{n}^0,\omega_{n}^{2}, \omega_{n}^{3}, \ldots, \omega_{n}^{n-1}\)
单位根的性质
(1)\(\omega_{n}^{k}=\cos k * \frac{2 \pi}{n}+i \sin k * \frac{2 \pi}{n}\)
(2)\(\omega_{2 n}^{2 k}=\omega_{n}^{k}\)
(3)\(\omega_{n}^{k+\frac{n}{2}}=-\omega_{n}^{k}\)
(4)\(\omega_{n}^{0}=\omega_{n}^{n}=1\)
根据上述四条性质,就可以进行快速的系数与点值之间的转换。
快速傅里叶变换
系数到点值的快速转换
对于一个用系数表示的多项式:
我们可以将每一项按幂次的奇偶进行拆分:
设
那么不难得到
我们将 \(\omega_{n}^{k}\left(k<\frac{n}{2}\right)\) 代入得
同理, 将 \(\omega_{n}^{k+\frac{n}{2}}\) 代入得
此时可以发现, \(\omega_{n}^{k}\) 和 \(\omega_{n}^{k+\frac{n}{2}}\)相差的只是一个系数,大头的两个子多项式是完全一样的,因此只要算出了\(A_{1}\left(\omega_{\frac{n}{2}}^{k}\right)\)和\(A_{2}\left(\omega_{\frac{n}{2}}^{k}\right)\)就可以得到\(\omega_{n}^{k}\) 和 \(\omega_{n}^{k+\frac{n}{2}}\)。整体来看,得到了\(A_1\)和\(A_2\)的点值表示法就可以\(O(n)\)地得出\(A\)的点值表示法,同时\(A_1\)和\(A_2\)也可以用同样的方法得到,这就变成了一个每次将规模缩小为\(1/2\)的递归过程。显然递归的深度为\(log_2n\),整体的时间复杂度就是\(O(n*logn)\)
点值到系数的快速转换
设\(\left(y_{0}, y_{1}, y_{2}, \ldots, y_{n-1}\right)\) 为 \(\left(a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}\right)\) 的傅里叶变换 (即点值表示)
设有另一个向量 \(\left(c_{0}, c_{1}, c_{2}, \ldots, c_{n-1}\right)\) 满足
即多项式 \(B(x)=y_{0}, y_{1} x, y_{2} x^{2}, \ldots, y_{n-1} x^{n-1}\) 在 \(\omega_{n}^{0}, \omega_{n}^{-1}, \omega_{n}^{-2}, \ldots, \omega_{n-1}^{-(n-1)}\) 处的点值表示
可以证明,\(c_k=na_k\),因此点值到系数的转换只要做一次类似系数到点值转换的过程就可以了,时间复杂度也是\(O(n*logn)\)
迭代法
根据上述原理已经可以用递归的方法写出\(O(n*logn)\)的多项式乘法了,但是空间复杂度也是\(O(nlogn)\),下面给出一种优化空间复杂度为\(O(n)\)的迭代方法。
观察原来的递归过程:
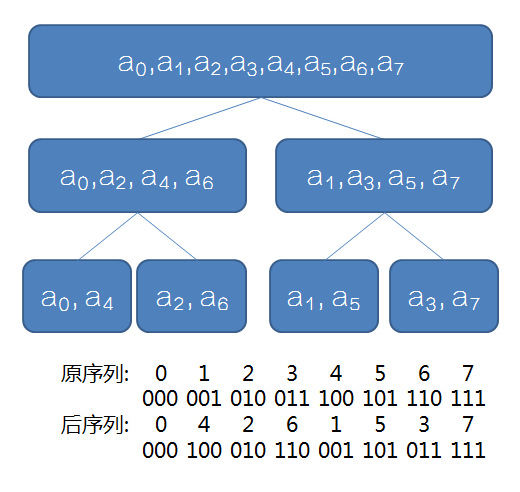
可以发现,我们需要求的序列是原序列下标的二进制反转,因此我们可以借助这个性质\(O(n)\)地得出反转后的序列,直接不停地合并即可
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const double pi=acos(-1.0);
struct cp{
double x,y;
cp(){x=y=0;}
cp(double xx,double yy){x=xx,y=yy;}
};
cp operator + (cp a,cp b){
return cp(a.x+b.x,a.y+b.y);
}
cp operator - (cp a,cp b){
return cp(a.x-b.x,a.y-b.y);
}
cp operator * (cp a,cp b){
return cp(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
inline void FFT(int n,vector<cp> &a,int t,vector<int> &rev){//迭代版FFT
for(int i=0;i<=n-1;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=1;len<=(n>>1);len<<=1){
cp w1(cos(pi/len),t*sin(pi/len));
for(int i=0;i<=n-(len<<1);i+=(len<<1)){
cp w(1,0);
for(int j=0;j<=len-1;j++){
cp x=a[i+j],y=w*a[i+j+len];
a[i+j]=x+y,a[i+j+len]=x-y;
w=w*w1;
}
}
}
}
void solve(vector<int>&a,vector<int>&b,vector<int>&res){
int n,m;
n=a.size()-1,m=b.size()-1;
int k=1,ci=0;
while(k<=n+m)k<<=1,ci++;
vector<int> rev(k+1,0);
vector<cp> f(k+1),g(k+1);
for(int i=0;i<=n;i++)f[i].x=a[i];
for(int i=0;i<=m;i++)g[i].x=b[i];
for(int i=1;i<=k-1;i++)//二进制翻转
rev[i]=(rev[i>>1]>>1)|((i&1)<<(ci-1));
FFT(k,f,1,rev);
FFT(k,g,1,rev);
for(int i=0;i<=k;i++)
f[i]=f[i]*g[i];
FFT(k,f,-1,rev);
for(int i=0;i<=n+m;i++)
res[i]=(int)(f[i].x/k+0.5);
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
vector<int> a(n+1),b(m+1),res(n+m+1);
for(int i=0;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=0;i<=m;i++){
scanf("%d",&b[i]);
}
solve(a,b,res);
for(int i=0;i<=n+m;i++){
if(i>0)printf(" ");
printf("%d",res[i]);
}
return 0;
}
NTT
由于原根具有和单位根类似的性质,我们可以用原根来代替单位根,使计算没有精度的误差。
和将单位圆进行等分一样,这里是把一个大小为p-1的群进行等分(\(g^0,g^1,g^2...g^{p-1}\)),由于每次迭代都是/2的过程,这里等分也和单位圆一样要分成2的幂次份,因此P的选取是有要求的,必须是像\(r∗2^k+1\)这样的形式,这样分最多能分成\(2^k\)份。
之后只要将\(Wn\)用\(g^{\frac{p-1}{n}}\)替换即可。
P可以取998244353,原根g=3,\(998244353=119*2^{23}+1\),最大可以支持\(n+m=2^{23}\)的多项式乘法运算。但是需要注意的是答案的系数必须小于998244353,否则得到的就是取模后的值,不是真值。
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const ll P=998244353,G=3,Gi=332748118;
ll fp(ll b,ll p,ll mod){
ll ans=1;
while(p){
if(p&1)ans=ans*b%mod;
b=b*b%mod;
p>>=1;
}
return ans;
}
ll inv(ll x,ll mod){
return fp(x,mod-2,mod);
}
inline void NTT(int n,vector<ll> &a,int t,vector<int> &rev){//迭代版FFT
for(int i=0;i<=n-1;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int len=1;len<=(n>>1);len<<=1){
ll w1 = fp( t == 1 ? G : Gi , (P - 1) / (len << 1) , P);
for(int i=0;i<=n-(len<<1);i+=(len<<1)){
ll w=1;
for(int j=0;j<=len-1;j++){
ll x=a[i+j],y=w*a[i+j+len]%P;
a[i+j]=(x+y)%P,a[i+j+len]=(x-y+P)%P;
w=w*w1%P;
}
}
}
}
void solve(vector<int>&a,vector<int>&b,vector<int>&res){
int n,m;
n=a.size()-1,m=b.size()-1;
int k=1,ci=0;
while(k<=n+m)k<<=1,ci++;
vector<int> rev(k+1,0);
vector<ll> f(k+1),g(k+1);
for(int i=0;i<=n;i++)f[i]=a[i]%P;
for(int i=0;i<=m;i++)g[i]=b[i]%P;
for(int i=1;i<=k-1;i++)//二进制翻转
rev[i]=(rev[i>>1]>>1)|((i&1)<<(ci-1));
NTT(k,f,1,rev);
NTT(k,g,1,rev);
for(int i=0;i<=k;i++)
f[i]=f[i]*g[i]%P;
NTT(k,f,-1,rev);
ll k_inv=inv(k,P);
for(int i=0;i<=n+m;i++)
res[i]=f[i]*k_inv%P;
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
vector<int> a(n+1),b(m+1),res(n+m+1);
for(int i=0;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=0;i<=m;i++){
scanf("%d",&b[i]);
}
solve(a,b,res);
for(int i=0;i<=n+m;i++){
if(i>0)printf(" ");
printf("%d",res[i]);
}
return 0;
}
MTT
如何做任意模数多项式乘法?可以用FFT,但是如果结果较大为了保证精度还是需要使用NTT。
先用三个不同模数的NTT做一遍,得到以下结果:
我们把前两个式子通过中国乘余定理合并, 就可以得到
其中, \(M=m_{1} * m_{2}\)
设\(ans =k M+A\),则
为了保证\(k\)的真值是小于\(m3\)的,则必须保证\(\frac{ans}{m_1*m_2}<m_3\),即\(ans<m_1m_2m_3\)。
这里用的三个模数为469762049,998244353,1004535809,可以运算的结果上限为\(4e20\)以内,\(n+m \le 2^{21}(2e6)\)的多项式运算。
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const ll p1=469762049,p2=998244353,p3=1004535809,G=3;
ll fm(ll b,ll p,ll mod){
ll ans=0;
b%=mod;
while(p){
if(p&1)ans=(ans+b)%mod;
b=(b+b)%mod;
p>>=1;
}
return ans;
}
ll fp(ll b,ll p,ll mod){
ll ans=1;
b%=mod;
while(p){
if(p&1)ans=ans*b%mod;
b=b*b%mod;
p>>=1;
}
return ans;
}
ll inv(ll x,ll mod){
return fp(x,mod-2,mod);
}
inline void NTT(int n,vector<ll> &a,int t,vector<int> &rev,int P){//迭代版FFT
for(int i=0;i<=n-1;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
ll Gi=inv(G,P);
for(int len=1;len<=(n>>1);len<<=1){
ll w1 = fp( t == 1 ? G : Gi , (P - 1) / (len << 1) , P);
for(int i=0;i<=n-(len<<1);i+=(len<<1)){
ll w=1;
for(int j=0;j<=len-1;j++){
ll x=a[i+j],y=w*a[i+j+len]%P;
a[i+j]=(x+y)%P,a[i+j+len]=(x-y+P)%P;
w=w*w1%P;
}
}
}
}
void cal(vector<int>&a,vector<int>&b,vector<int>&res,int P){
int n,m;
n=a.size()-1,m=b.size()-1;
int k=1,ci=0;
while(k<=n+m)k<<=1,ci++;
vector<int> rev(k+1,0);
vector<ll> f(k+1),g(k+1);
for(int i=0;i<=n;i++)f[i]=a[i]%P;
for(int i=0;i<=m;i++)g[i]=b[i]%P;
for(int i=1;i<=k-1;i++)//二进制翻转
rev[i]=(rev[i>>1]>>1)|((i&1)<<(ci-1));
NTT(k,f,1,rev,P);
NTT(k,g,1,rev,P);
for(int i=0;i<=k;i++)
f[i]=f[i]*g[i]%P;
NTT(k,f,-1,rev,P);
ll k_inv=inv(k,P);
res.resize(n+m+1);
for(int i=0;i<=n+m;i++)
res[i]=f[i]*k_inv%P;
}
void solve(vector<int>&a,vector<int>&b,vector<int>&res,int P){
vector<int>a1,a2,a3;
cal(a,b,a1,p1);
cal(a,b,a2,p2);
cal(a,b,a3,p3);
int n=a1.size();
res.resize(n);
ll M=p1*p2;
for(int i=0;i<n;i++){
ll A=0;
A+=fm(a1[i]*p2%M,inv(p2,p1),M);
A+=fm(a2[i]*p1%M,inv(p1,p2),M);
A%=M;
ll k=(((ll)a3[i]-A)%p3+p3)%p3*inv(M,p3)%p3;
res[i]=(k%P*(M%P)%P+A%P)%P;
}
}
int main(){
int n,m,p;
scanf("%d%d%d",&n,&m,&p);
vector<int> a(n+1),b(m+1),res(n+m+1);
for(int i=0;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=0;i<=m;i++){
scanf("%d",&b[i]);
}
solve(a,b,res,p);
for(int i=0;i<=n+m;i++){
if(i>0)printf(" ");
printf("%d",res[i]);
}
return 0;
}

