ICPC2019上海区域赛 部分题解(正在更新)
K. Color Graph
题意:
给定一个简单图,点个数<=16,删去部分边后,使得该图中无边数为奇数得环,问剩下的边数最大为多少?
思路:
如果一个图中无奇数边的环,那么这个图一定是个二分图。只要枚举二分图的左部,统计所有从左部到右部的边个数,答案就是枚举出的所有边数的最大值。(因为最优解一定也是一个二分图,所以一定会被枚举到)
//赛后补题,只过样例,仅供参考
#include <bits/stdc++.h>
using namespace std;
const int maxn=105;
const int maxm=1e4+5;
struct edge{
int u,v;
}E[maxm];
int tot=0;
void addedge(int u,int v){
E[++tot].u=u;
E[tot].v=v;
}
int color[maxn];
int main(){
int T;
cin>>T;
for(int kase=1;kase<=T;kase++){
int n,m;
scanf("%d%d",&n,&m);
fill(color,color+1+n,0);
tot=0;
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
addedge(u,v);
}
int ans=0;
for(int meijv=0;meijv<=(1<<n)-1;meijv++){
int mj=meijv;
for(int i=1;i<=n;i++){
if(mj&1){
color[i]=1;
}
else color[i]=0;
mj>>=1;
}
int res=0;
for(int i=1;i<=tot;i++){
if(color[E[i].u]!=color[E[i].v]){
res++;
}
}
ans=max(ans,res);
}
printf("Case #%d: %d\n",kase,ans);
}
}
D. Spanning Tree Removal
题意:
给定一个n阶的完全图,每次操作是从图中移除一棵生成树的所有边,问最多能进行多少次这样的操作?输出操作次数和每次移除的生成树的边。
思路:
n阶完全图共有n*(n-1)/2条边,一棵生成树有n-1条边,很容易猜到能进行n/2次操作,接下来就是如何构造的问题。
下面给出一种直接构造的方法(奇数就孤立出一个点随便连即可)
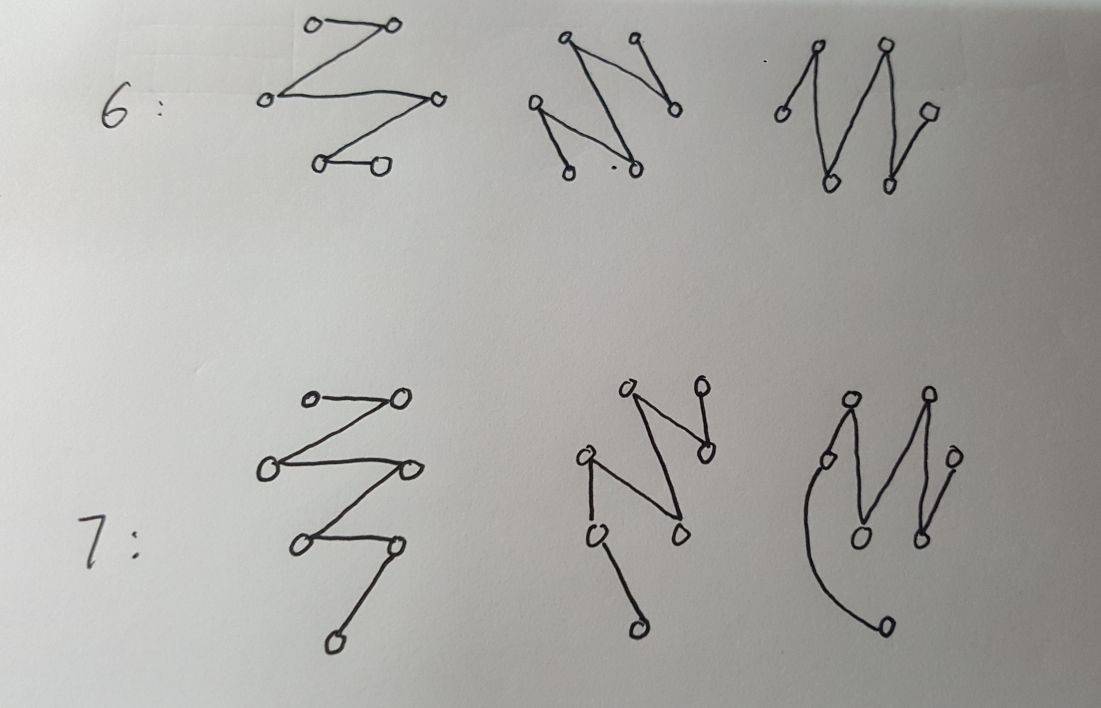
//赛后补题,只过样例,仅供参考
#include <bits/stdc++.h>
using namespace std;
int main(){
int T;
cin>>T;
for(int kase=1;kase<=T;kase++){
int n;
scanf("%d",&n);
printf("Case #%d: %d\n",kase,n/2);
if(n%2==0){
for(int i=1;i<=n/2;i++){
printf("%d %d\n",i,i+1);
for(int j=1;j<=n/2-1;j++){
int u=i+j;
int v=(u+n-j*2-1)%n+1;
printf("%d %d\n",u,v);
printf("%d %d\n",v,u+1);
}
}
}
else{
n--;
for(int i=1;i<=n/2;i++){
printf("%d %d\n",i,i+1);
for(int j=1;j<=n/2-1;j++){
int u=i+j;
int v=(u+n-j*2-1)%n+1;
printf("%d %d\n",u,v);
printf("%d %d\n",v,u+1);
}
printf("%d %d\n",i,n+1);
}
}
}
}
H. Tree Partition
题意:
给出一棵点权树,一个树的大小定义为所有点的权值和。问将一棵树分为k棵子树,如何分割才能使所有树的大小的最大值最小?
思路:
二分答案,已知最大连通子图的大小x后,只要在树上从树根向上dp子树的大小即可。如果一个子树u的大小大于x,则先选择u最大的儿子v切除(即切割边u,v),这样能保证剩下的部分大小尽可能地小。这样保证了图上所有的连通子图的都是小于x的,同时也是用贪心的方法选择切割方案(每个子树都尽可能地取到最大,使剩下部分尽可能小),得到的就是最小的切割次数。
实现方法:若判断发现一个节点u的权值大于x,则将他的儿子节点排序,从大到小依次删除,直到u的权值小于x。
//赛后还原,仅供参考
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;
struct edge{
int v,next;
}E[maxn];
int head[maxn],tot;
void addedge(int u,int v){
E[++tot].v=v;
E[tot].next=head[u];
head[u]=tot;
}
ll a[maxn],sum[maxn];
int flag=0,cnt;
int n,k;
void dfs(int u,int fa,ll x){
sum[u]=a[u];
if(sum[u]>x||flag==0){
flag=0;
return;
}
for(int i=head[u];i;i=E[i].next){
int v=E[i].v;
if(v!=fa){
dfs(v,u,x);
sum[u]+=sum[v];
}
}
if(sum[u]>x){
vector<ll>V;
for(int i=head[u];i;i=E[i].next){
int v=E[i].v;
if(v!=fa){
V.push_back(sum[v]);
}
}
sort(V.begin(),V.end());
while(sum[u]>x){
cnt++;
sum[u]-=V.back();
V.pop_back();
}
}
if(cnt>k-1){
flag=0;
return;
}
}
bool check(ll x){
flag=1;cnt=0;
dfs(1,0,x);
// printf("%lld:%d\n",x,flag);
if(flag)
return 1;
else
return 0;
}
int main(){
int T;
cin>>T;
for(int kase=1;kase<=T;kase++){
scanf("%d%d",&n,&k);
fill(head,head+1+n,0);
fill(sum,sum+1+n,0);
tot=0;
for(int i=1;i<=n-1;i++){
int u,v;
scanf("%d%d",&u,&v);
addedge(u,v);
addedge(v,u);
}
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
ll l=0,r=1e14+5;//左开右闭
while(r-l>1){
ll mid=(r+l+1)/2;
if(check(mid))
r=mid;
else
l=mid;
}
printf("Case #%d: %lld\n",kase,r);
}
}
E. Cave Escape
题意:
给定一个\(n * m\)的格子矩阵,其中有一个格子是起点,一个格子是终点。从起点开始移动,每次能移动到有相邻边的格子中,每个格子都有一个权值v,若从点a移动到点b,且b点未被访问过,则可以获得\(Va*Vb\)的收益,若移动到终点,可以选择先不出去,继续在图上乱走,问如何可以使得走出终点后获得得收益最大?(只需要输出最大收益即可)
思路:
很显然终点在哪是对答案完全没有影响的,只要在矩阵中乱走获得最大收益再出去即可。
我们可以将这个矩阵转化为一个无向图,图中的点就是矩阵的格点,相邻格点之间有一条边,长度为它们权值的乘积。只要在这个图上跑一遍最大生成树,树的大小就是最大收益。为什么起点也是对答案没有影响?因为要达到最大收益,最好的方法就是将图中每一个都遍历一遍,因为多遍历一个点是不会亏的,可以通过已经遍历到的任意点往新的点走来得到收益(已经遍历过的格子在矩阵中是连通的,可以到处转移),这不就是生成树吗?
//赛后补题,只过样例,仅供参考
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e3+5;
const int maxm=4e6+5;
struct edge{
int u,v;
ll w;
}E[maxm];
bool cmp(edge a,edge b){
return a.w>b.w;
}
int tot=0;
void addedge(int u,int v,ll w){
E[++tot].u=u;
E[tot].v=v;
E[tot].w=w;
}
int fa[maxn*maxn];
int n,m;
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
ll kruskal(){
for(int i=1;i<=n*m;i++){
fa[i]=i;
}
sort(E+1,E+1+tot,cmp);
int cnt=0;
ll ans=0;
for(int i=1;i<=tot;i++){
int u=E[i].u;
int v=E[i].v;
int fu=find(u);
int fv=find(v);
if(fu!=fv){
fa[fu]=fv;
ans+=E[i].w;
cnt++;
}
if(cnt==n*m-1)return ans;
}
}
ll x[maxn*maxn];
ll V[maxn][maxn];
int xx[]={1,0,0,-1};
int yy[]={0,1,-1,0};
int main(){
int T;
cin>>T;
for(int kase=1;kase<=T;kase++){
int sr,sc,tr,tc;
scanf("%d%d%d%d%d%d",&n,&m,&sr,&sc,&tr,&tc);
tot=0;
ll A,B,C,P;
scanf("%lld%lld%lld%lld%lld%lld",&x[1],&x[2],&A,&B,&C,&P);
for(int i=3;i<=n*m;i++){
x[i]=(x[i-1]*A+x[i-2]*B+C)%P;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
V[i][j]=x[(i-1)*m+j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int pp=0;pp<4;pp++){
int it=i+xx[pp];
int jt=j+yy[pp];
int u=(i-1)*m+j;
int v=(it-1)*m+jt;
if(it>=1&&it<=n&&jt>=1&&jt<=m){
addedge(u,v,V[i][j]*V[it][jt]);
}
}
}
}
ll ans=kruskal();
printf("Case #%d: %lld\n",kase,ans);
}
}
B. Prefix Code
题意:
给出一系列数字,长度均小于10,问是否有一个数是其他数的前缀?
思路:
Trie树模板题。记录单词的终末,前缀包含的单词个数即可。若一个点是单词终末且前缀包含单词个数>1,则输出No。
//输入字串用s+1,函数调用用s
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int T[maxn][12];
int num[maxn];
int isend[maxn];
int tot=1;
void add(char *s){
int l=strlen(s+1);
int rt=1;
for(int i=1;i<=l;i++){
if(T[rt][s[i]-'0']==0){
T[rt][s[i]-'0']=++tot;
rt=tot;
}
else{
rt=T[rt][s[i]-'0'];
}
num[rt]++;
}
isend[rt]=1;
}
void init(){
for(int i=0;i<=tot;i++){
memset(T[i],0,sizeof(T[i]));
num[i]=isend[i]=0;
}
tot=1;
}
char s[15];
int main(){
int T;
cin>>T;
for(int kase=1;kase<=T;kase++){
init();
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%s",s+1);
add(s);
}
int flag=1;
for(int i=1;i<=tot;i++){
if(isend[i]&&num[i]>1){
flag=0;
break;
}
}
if(flag)
printf("Case #%d: Yes\n",kase);
else
printf("Case #%d: No\n",kase);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号