poj 2049 -- Finding Nemo

Finding Nemo

Time Limit: 2000MS		Memory Limit: 30000K
Total Submissions: 7372		Accepted: 1714

Description

Nemo is a naughty boy. One day he went into the deep sea all by himself. Unfortunately, he became lost and couldn't find his way home. Therefore, he sent a signal to his father, Marlin, to ask for help.
After checking the map, Marlin found that the sea is like a labyrinth with walls and doors. All the walls are parallel to the X-axis or to the Y-axis. The thickness of the walls are assumed to be zero.
All the doors are opened on the walls and have a length of 1. Marlin cannot go through a wall unless there is a door on the wall. Because going through a door is dangerous (there may be some virulent medusas near the doors), Marlin wants to go through as few doors as he could to find Nemo.
Figure-1 shows an example of the labyrinth and the path Marlin went through to find Nemo.

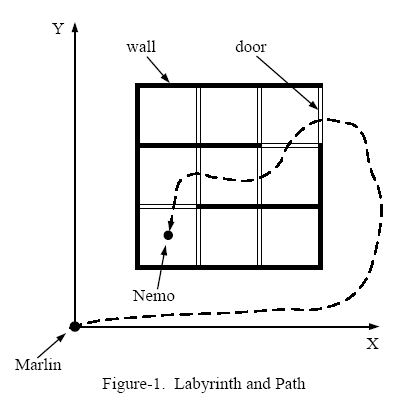
We assume Marlin's initial position is at (0, 0). Given the position of Nemo and the configuration of walls and doors, please write a program to calculate the minimum number of doors Marlin has to go through in order to reach Nemo.

Input

The input consists of several test cases. Each test case is started by two non-negative integers M and N. M represents the number of walls in the labyrinth and N represents the number of doors.
Then follow M lines, each containing four integers that describe a wall in the following format:
x y d t
(x, y) indicates the lower-left point of the wall, d is the direction of the wall -- 0 means it's parallel to the X-axis and 1 means that it's parallel to the Y-axis, and t gives the length of the wall.
The coordinates of two ends of any wall will be in the range of [1,199].
Then there are N lines that give the description of the doors:
x y d
x, y, d have the same meaning as the walls. As the doors have fixed length of 1, t is omitted.
The last line of each case contains two positive float numbers:
f1 f2
(f1, f2) gives the position of Nemo. And it will not lie within any wall or door.
A test case of M = -1 and N = -1 indicates the end of input, and should not be processed.

Output

For each test case, in a separate line, please output the minimum number of doors Marlin has to go through in order to rescue his son. If he can't reach Nemo, output -1.

Sample Input

Sample Output

5
-1

这个题光建图就坑了我很长时间，orz。。
大体意思是儿子掉水里了，爸爸去救，爸爸发现这片水域像个迷宫，有墙有门还有空地，问他爸爸最少经过几道门才能救出他儿子。

拿测试数据来说明我的建图方式：
　　x y d t  表示坐标为xy，d表示平行于哪个坐标轴，t表示这个方向上的长度
来看图

我们以Nemo方格点为(1,1)  它上面的点为（1,2)，这样以此类推，每个方格用一个3维数组表示： d[x][y][4] ,x,y表示坐标，4分别表示上左下右四个方向，
而d[x][y][x] 表示x方向上是门，是墙还是空地。
而建图的过程就是
void BuildGrap()
{
    for(int i = 0; i < 200; i++){
        for(int j = 0; j < 200; j++){
            d[i][j][0] = s[i][j+1][0];
            d[i][j][1] = s[i+1][j][1];
            d[i][j][3] = s[i][j][0];
            d[i][j][2] = s[i][j][1];

        }
    }
}
此外此题我是倒着做的，从nemo所处位置开始搜索，一直搜到最外围，然后可能存在多种情况，所以用优先队列可以确定第一个到达外围的步数。

  1 /*======================================================================
  2  *           Author :   kevin
  3  *         Filename :   FindingNemo.cpp
  4  *       Creat time :   2014-05-26 20:27
  5  *      Description :
  6 ========================================================================*/
  7 #include <iostream>
  8 #include <algorithm>
  9 #include <cstdio>
 10 #include <cstring>
 11 #include <queue>
 12 #include <cmath>
 13 #define clr(a,b) memset(a,b,sizeof(a))
 14 #define M 205
 15 #define INF 0x7f7f7f7f
 16 using namespace std;
 17 int d[M][M][4],s[M][M][2];
 18 int vis[M][M],cnt[M][M];
 19 int lastx,lasty,maxx,maxy;
 20 int dir[4][2] = {{0,1},{1,0},{-1,0},{0,-1}};
 21 struct Node     //优先队列，按cnt统计的步数排序
 22 {
 23     int x,y;
 24     bool operator < (const Node &a) const{
 25         return cnt[a.x][a.y] < cnt[x][y];
 26     }
 27 }node;
 28 void BFS()
 29 {
 30     priority_queue<Node>que;
 31     Node temp;
 32     node.x = lastx; node.y = lasty;
 33     que.push(node);
 34     vis[lastx][lasty] = 1;
 35     while(que.empty() != true){
 36         int x,y;
 37         temp = que.top();
 38         que.pop();
 39         for(int i = 0; i < 4; i++){
 40             x = temp.x + dir[i][0]; y = temp.y + dir[i][1];
 41             if(x < 0 || y < 0) continue;
 42             if(x > 199 || y > 199) continue;
 43             if(d[x][y][3-i] != 1){  //若不是墙
 44                 node.x = x; node.y = y;
 45                 if(d[x][y][3-i] == 0){  //若是门
 46                     if(vis[x][y]) //若被访问过，更新cnt值
 47                         cnt[x][y] = min(cnt[x][y],cnt[temp.x][temp.y]+1);
 48                     else{
 49                         cnt[x][y] = cnt[temp.x][temp.y]+1;
 50                         que.push(node);
 51                     }
 52                 }
 53                 else{ //若是空地
 54                     if(vis[x][y])//若被访问过，更新cnt值
 55                         cnt[x][y] = min(cnt[x][y],cnt[temp.x][temp.y]);
 56                     else{
 57                         cnt[x][y] = cnt[temp.x][temp.y];
 58                         que.push(node);
 59                     }
 60                 }
 61                 vis[x][y] = 1; //访问标记
 62                 if(x > maxx || y > maxy){ //达到边界，将步数更新到cnt[0][0]
 63                     cnt[0][0] = min(cnt[0][0],cnt[x][y]);
 64                     break;
 65                 }
 66             }
 67         }
 68     }
 69 }
 70 void BuildGrap()  //建图
 71 {
 72     for(int i = 0; i < 200; i++){
 73         for(int j = 0; j < 200; j++){
 74             d[i][j][0] = s[i][j+1][0];
 75             d[i][j][1] = s[i+1][j][1];
 76             d[i][j][3] = s[i][j][0];
 77             d[i][j][2] = s[i][j][1];
 78 
 79         }
 80     }
 81 }
 82 int main(int argc,char *argv[])
 83 {
 84     int n,m,a,b,dd,t;
 85     double xx,yy;
 86     while(scanf("%d%d",&n,&m)!=EOF){
 87         clr(d,-1);
 88         clr(s,-1);
 89         clr(vis,0);
 90         clr(cnt,0);
 91         if(n == -1 && m == -1) break;
 92         maxx = maxy = 0;
 93         for(int i = 0; i < n; i++){
 94             scanf("%d%d%d%d",&a,&b,&dd,&t);
 95             if(dd == 1){
 96                 for(int k = 0; k < t; k++){
 97                     s[a][b][dd] = 1;
 98                     b++;
 99                 }
100             }
101             if(dd == 0){
102                 for(int k = 0; k < t; k++){
103                     s[a][b][dd] = 1;
104                     a++;
105                 }
106             }
107             if(maxx < a){
108                 maxx = a;
109             }
110             if(maxy < b){
111                 maxy = b;
112             }
113         }
114         for(int i = 0; i < m; i++){
115             scanf("%d%d%d",&a,&b,&dd);
116             s[a][b][dd] = 0;
117         }
118         scanf("%lf%lf",&xx,&yy);
119         lastx = floor(xx);
120         lasty = floor(yy);
121         if(lastx < 0 || lastx > 199 || lasty < 0 || lasty > 199){
122             printf("0\n");
123             continue;
124         }
125         BuildGrap();
126         cnt[0][0] = INF;
127         BFS();
128         if(cnt[0][0] == INF){
129             printf("-1\n");
130         }
131         else{
132             printf("%d\n",cnt[0][0]);
133         }
134     }
135     return 0;
136 }