板子-补充
Pollard_Rho
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
typedef long long ll;
const int maxn = 105;
ll x[maxn], ans;
ll factor[maxn];
ll multi(ll a, ll b, ll p) //快速乘
{
__int128 tmp1=a,tmp2=b,tmp3=p;
return tmp1*tmp2%tmp3;
}
ll qpow(ll a, ll b, ll p)
{
ll ans = 1;
while(b){
if(b & 1LL) ans = multi(ans, a, p);
a = multi(a, a, p);
b >>= 1;
}
return ans;
}
bool MR(ll n)
{
if(n == 2) return true;
int s = 20, i, t = 0;
ll u = n-1;
while(!(u&1)){
t++;
u >>= 1;
}
while(s--){
ll a = rand()%(n-2)+2;
x[0] = qpow(a, u, n);
for(i = 1; i <= t; i++){
x[i] = multi(x[i-1], x[i-1], n);
if(x[i] == 1 && x[i-1] != 1 && x[i-1] != n-1) return false;
}
if(x[t] != 1) return false;
}
return true;
}
ll gcd(ll a, ll b)
{
if(b == 0) return a;
else return gcd(b, a%b);
}
//ll gcd(ll a,ll b){
// return __gcd(a,b);
//}
ll Pollard_Rho(ll n, int c)
{
ll i = 1, k = 2, x = rand()%(n-1)+1, y = x;
while(1){
i++;
x = (multi(x, x, n)+c)%n;
ll p = gcd((y-x+n)%n, n);
if(p != 1 && p != n) return p;
if(y == x) return n;
if(i == k){
y = x;
k <<= 1;
}
}
}
void find(ll n, int c)
{
if(n == 1) return;
if(MR(n)){
factor[++factor[0]]=n;
return;
}
ll p = n, k = c;
while(p >= n){
p = Pollard_Rho(p, c--);
}
find(p, k);
find(n/p, k);
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0);
srand(time(0));
ll t,n;
cin>>t;
for(int cs=1;cs<=t;++cs){
cin>>n;
factor[0]=0;
find(n,107);
if(factor[0]==1){
cout<<"Prime\n";
}
else{
ll tmp=factor[1];
for(int i=2;i<=factor[0];++i){
if(factor[i]>tmp)tmp=factor[i];
}
cout<<tmp<<'\n';
}
}
return 0;
}
最大团
复杂度 \(O(3^n)\).
最大团点的数量=补图中最大独立集点的数量
图的染色问题中,最少需要的颜色的数量=最大团点的数量
const int maxn = 130;
bool mp[maxn][maxn]; //邻接矩阵
int some[maxn][maxn], none[maxn][maxn], all[maxn][maxn];
int n, m, ans;
void dfs(int d, int an, int sn, int nn)
{
if(!sn && !nn) ans = max(ans, an);
int u = some[d][0];
for(int i = 0; i < sn; ++i)
{
int v = some[d][i];
if(mp[u][v]) continue;
for(int j = 0; j < an; ++j)
all[d+1][j] = all[d][j];
all[d+1][an] = v;
int tsn = 0, tnn = 0;
for(int j = 0; j < sn; ++j)
if(mp[v][some[d][j]])
some[d+1][tsn++] = some[d][j];
for(int j = 0; j < nn; ++j)
if(mp[v][none[d][j]])
none[d+1][tnn++] = none[d][j];
dfs(d+1, an+1, tsn, tnn);
some[d][i] = 0, none[d][nn++] = v;
}
}
int work()
{
ans = 0;
for(int i = 0; i < n; ++i) some[1][i] = i+1;
dfs(1, 0, n, 0);
return ans;
}
三元环计数
无向图
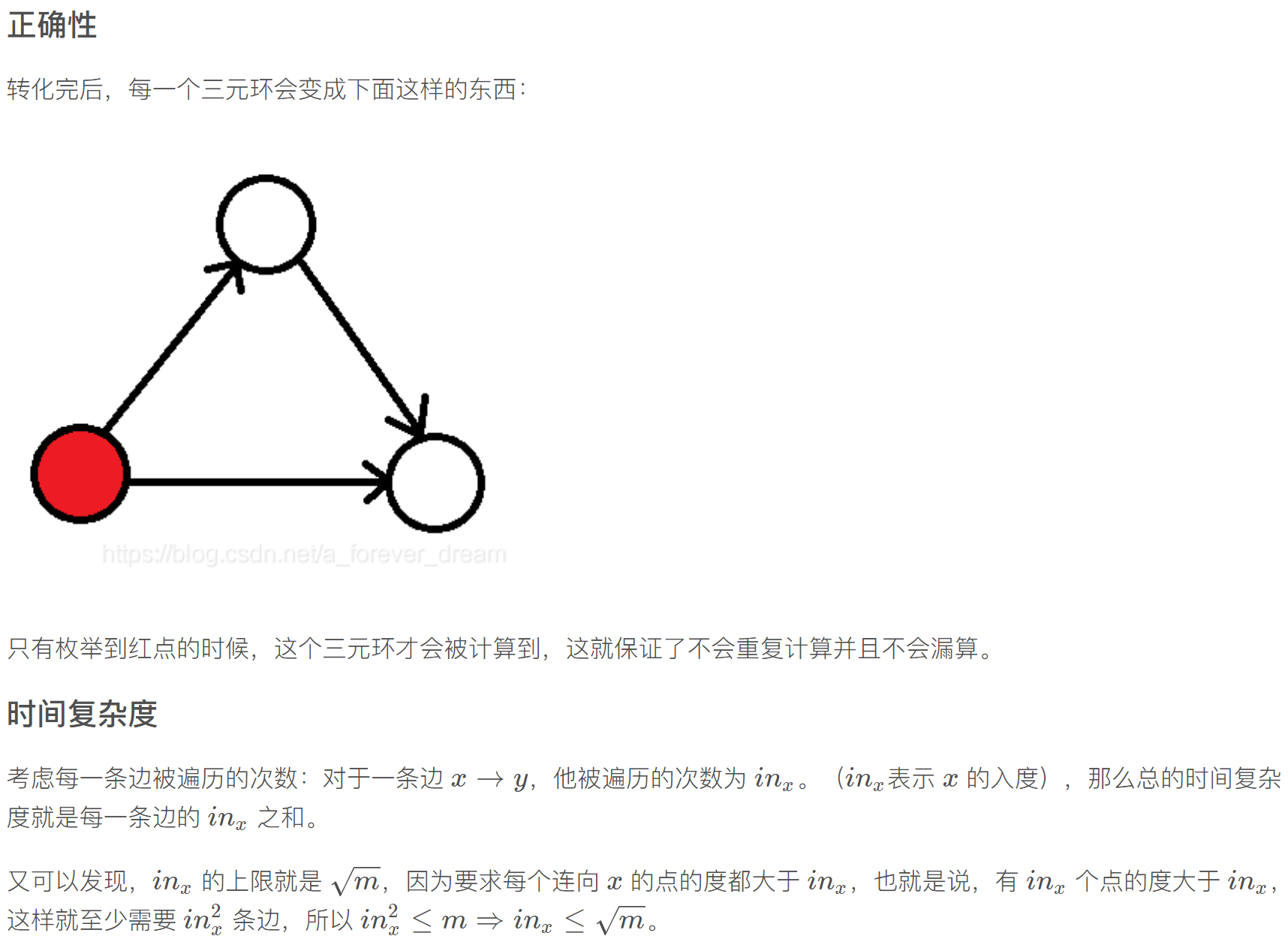
时间复杂度 \(\text O(m\sqrt{m})\)
https://blog.csdn.net/a_forever_dream/article/details/101441587


#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define maxn 300010
#define ll long long
int n,m;
struct edge{int y,next;};
edge e[maxn*4];
int len;
int first[maxn];
void buildroad(int x,int y)
{
e[++len]=(edge){y,first[x]};
first[x]=len;
}
struct node{int x,y;};
node edges[maxn*2];
int du[maxn],id[maxn],to[maxn],tot[maxn];
inline ll C(int x){return (ll)x*(x-1)/2ll;}
int main()
{
while(~scanf("%d %d",&n,&m))
{
memset(du,0,sizeof(du));//记录每个点的度的数组
for(int i=1;i<=m;i++)
scanf("%d %d",&edges[i].x,&edges[i].y),du[edges[i].x]++,du[edges[i].y]++;
memset(first,0,sizeof(first));len=0;
for(int i=1,x,y;i<=m;i++)
{
x=edges[i].x,y=edges[i].y;
if(x>y)swap(x,y);//让x成为编号小的点
if(du[x]>=du[y])buildroad(x,y);//度大的往小的连有向边
else buildroad(y,x);
}
memset(tot,0,sizeof(tot));//别忘了初始化各种数组
memset(to,0,sizeof(to));//to[i]表示当前点到点i的边是第几条边
memset(id,0,sizeof(id));//id表示每个点的标记
for(int i=1;i<=n;i++)
{
int x=i;
for(int j=first[x];j;j=e[j].next)//枚举能到达的点,给他们大商标机
id[e[j].y]=x,to[e[j].y]=j;//打标记,记录to
for(int j=first[x];j;j=e[j].next)//再次遍历所有有标记的点
{
for(int k=first[e[j].y];k;k=e[k].next)//遍历有标记的点能到达的点
if(id[e[k].y]==x)tot[j]++,tot[k]++,tot[to[e[k].y]]++;
//假如能到达一个有标记的点,那么就找到了一个三元环,给这三条边都打上标记
}
}
ll ans=0;
for(int i=1;i<=len;i++)//统计答案
ans+=C(tot[i]);
printf("%lld\n",ans);
}
}
竞赛图
有向完全图的三元环计数
\(C(n,3)-\sum_{u} C(in_u,2)\) ,\(in_u\) 表示 \(u\) 的入度。


