[模板] 后缀自动机&&后缀树
后缀自动机
后缀自动机是一种确定性有限状态自动机, 它可以接收字符串\(s\)的所有后缀.
构造, 性质
翻译自毛子俄罗斯神仙的博客, 讲的很好
后缀自动机详解 - DZYO的博客 - CSDN博客
下面是一些note:
定义
- 对于字符串\(s\)的子串\(t\), \(endpos(t)\) (或者 \(right(t)\) ) 表示t在s中出现位置的右端点的集合.
- \(endpos\)互不相交.
- 有相同 \(endpos\) 集合的字符串构成一个等价类.
- 对于每个等价类, 包含的字符串长度为\([len(p), maxlen(p)]\) , 是一个连续的区间.
- 后缀自动机的节点 \(p\) 代表一个 \(endpos\) 相同的子串的集合.
- 对于后缀自动机的节点 \(p\), \(parent(p)\) (或者 \(link(p)\) ) 表示p在不同等价类中的最长后缀.
- \(parent\) 形成一棵树关系.
- \(len(p) = maxlen(parent(p)) +1\)
构建 && 状态数/转移数线性证明
上面的blog已经写的很好了, 我就不重写一遍了:P
示意图
字符串 ab:
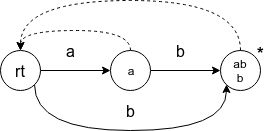
其中 * 代表终止节点, 虚箭头表示 \(fa(p)\).
字符串 abb:
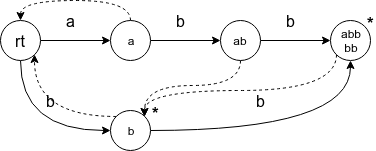
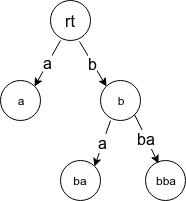
字符串 bba 的后缀树 (见后), 即字符串 abb 的前缀树/后缀自动机的 parent 树:
Code
const int nsz=1e6+50,ndsz=2*nsz,csz=27;
ll n;
char s[nsz];
//sam
//p.l means maxlen(p)
struct tnd{int ch[csz],l,fa,cnt;}sam[ndsz];
#define ch(p,c) sam[p].ch[c]
#define fa(p) sam[p].fa
int ps=1,las=1;
int cnt[ndsz],c[ndsz],seq[ndsz];
void insert(int c){
int p=las;
las=++ps,sam[las].l=sam[p].l+1,cnt[las]=1;
for(;p&&ch(p,c)==0;p=fa(p))ch(p,c)=las;
if(p==0)fa(las)=1;
else{
int q=ch(p,c);
if(sam[q].l==sam[p].l+1)fa(las)=q;
else{
int q1=++ps;
sam[q1]=sam[q],sam[q1].l=sam[p].l+1,fa(q)=fa(las)=q1;
for(;p&&ch(p,c)==q;p=fa(p))ch(p,c)=q1;
}
}
}
void build(){
rep(i,1,n)insert(s[i]-'a');
}
struct te{int t,pr;}edge[ndsz];
int hd[ndsz],pe=1;
void adde(int f,int t){edge[++pe]=(te){t,hd[f]};hd[f]=pe;}
void buildtr(){
rep(i,2,ps)adde(fa(i),i);
}
void gettp(){ //topo sort
rep(i,1,ps)++c[sam[i].l];
rep(i,1,ps)c[i]+=c[i-1];
rep(i,1,ps)seq[c[sam[i].l]--]=i;
}
void match(char *s,int n){
int cur=1,l=0;
rep(i,1,n){
if(ch(cur,s[i])){++l,cur=ch(cur,s[i]);}
else{
while(cur&&ch(cur,s[i])==0)cur=fa(cur);
if(cur==0)l=0,cur=1;
else l=sam[cur].l+1,cur=ch(cur,s[i]);
}
}
}
后缀树
后缀树是对字符串 \(S\) 的所有后缀建立的trie树, 同样可以识别 \(S\) 的所有后缀.
为了节省空间, 可以利用虚树的思想. 我们把只有一个子节点的节点压缩到它的父亲, 也就是说, 把没有分叉的一条链压缩成一条边.
显然, 这样建成的后缀 trie 只会保留每个后缀的终止节点('\0'), 和他们的lca. 这两者数量都是 \(O(n)\) 的, 因此状态总数也为 \(O(n)\) .
同时, 字符串 \(S\) 后缀自动机的parent树等价于 \(S\) 逆序 \(S'\) 的后缀树, 可以称作前缀树. 证明见[3].
几个关键问题
在后缀自动机上走路的时间复杂度
23333
就是说对字符串 \(S\) 建立后缀自动机, 然后将字符串 \(T\) 从起点走转移边, 如果没有转移边则跳parent指针. 这样可以求出 \(S\) 与 \(T\) 的每一个公共子串.
记当前 \(S\) 与 \(T\) 的匹配长度为 \(l\). 对于每一次转移, \(l\) 会加 \(1\); 对于跳parent指针, \(l\) 会减少, 而 \(l\) 总的减少不会超过 \(|T|\). 因此总时间复杂度为 \(O(|T|)\).
事实上, 对于insert(c)的均摊时间复杂度的分析是类似的.
代码
//l : max len of current matched string
//p : current state
void match(char *s,int n){
int cur=1,l=0;
rep(i,1,n){
if(ch(cur,s[i])){++l,cur=ch(cur,s[i]);}
else{
while(cur&&ch(cur,s[i])==0)cur=fa(cur);
if(cur==0)l=0,cur=1;
else l=sam[cur].l+1,cur=ch(cur,s[i]);
}
}
}
拓扑序
from [2]
SAM 中的 DAWG 满足一个性质,如果有一条转移边 \(u \rightarrow v\) ,则一定有 \(|\max(u)| < |\max(v)|\)。类似的,如果 \(\text{next}(v) = u\),也有 \(|\max(u)| < |\max(v)|\)。所以,按照每个节点记录的 max 长度排序,可以同时得到 DAWG 和前缀树的拓扑序。
使用桶排序, 那么时间复杂度是\(O(n)\).
代码
void gettp(){ //topo sort
rep(i,1,ps)++c[sam[i].l];
rep(i,1,ps)c[i]+=c[i-1];
rep(i,1,ps)seq[c[sam[i].l]--]=i;
}
这样我们就可以在SAM上进行动态规划.
每个节点代表字符串个数
由定义可知,
节点 \(p\) 代表字符串个数 $ = maxlen(p)-len(p)+1 = maxlen(p)-maxlen(parent(p))$.
同时, 节点 \(p\) 代表字符串个数 = 起点到节点 \(p\) 路径数.
求endpos集合
记非拷贝而来的节点为实节点, 否则为虚节点.
当实节点为第 \(t\) 个字符加入时建立的时, 它的endpos集合中显然有 \(t\), 并且它是endpos集合中有 \(t\) 的节点中maxlen最大的.
那么它的parent节点显然也包含\(t\), 直接跳parent()即可.
这时我们可以O(n)的求出endpos集合的大小:
- 对于不是拷贝的节点, cnt设为1; 拷贝而来的节点, cnt设为0.
- 在parent树上dp, \(cnt_p+=\sum_{parent(v)=p} cnt_v\).
- \(cnt_p\) 表示这个节点endpos集合大小, 也就是在字符串中的出现次数.
如果要求endpos集合, 需要可合并数据结构 (线段树/set/堆等). 利用可持久化线段树合并 ([模板] 线段树合并) 可以求出所有点的 endpos 集合.
最小表示法
建立\(S+S\)的后缀自动机, 从起点开始, 每次走字典序最小的转移, 并记录.
转移 \(|S|\) 次之后, 得到的字符串即为 \(S\) 的最小表示.
后缀自动机的用法
- 拓扑序 dp (自动机上/parent树上)
- 利用 len 函数和 endpos 集合 (dp, 线段树合并等)
- 利用 parent 树
- 树上的技巧: lca, 倍增, 点分治, 树剖, LCT
- dp(自上向下, 自下向上, 双重, 倍增)
- 利用自动机的性质 (转移等)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号