凸问题、分类器
时间好快;我想起去年一个南开同学做的凸问题的报告。
下边是知乎的一个朋友写的,贴过来用用^_^: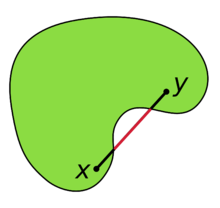
数学中最优化问题的一般表述是求取,使
,其中
是n维向量,
是
的可行域,
是
上的实值函数。
是 凸集是指对集合中的任意两点
,有
,即任意两点的连线段都在集合内,直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集,则涉及到闭集的定义,而闭集的定义又基于开集,比较抽象,不赘述,这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。
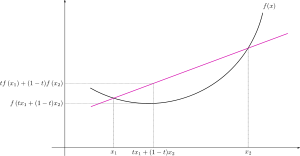
是凸函数是指对于定义域
中任意两点
,有
,直观上就是
向下凸出,如下图示意。
实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点:
- 目标函数
如果不是凸函数,则不是凸优化问题
- 决策变量
中包含离散变量(0-1变量或整数变量),则不是凸优化问题
- 约束条件写成
时,
如果不是凸函数,则不是凸优化问题
之所以要区分凸优化问题和非凸的问题原因在于凸优化问题中局部最优解同时也是全局最优解,这个特性使凸优化问题在一定意义上更易于解决,而一般的非凸最优化问题相比之下更难解决。
**************
看了上面的,我个人认为,所谓的凸优化问题,似乎可以用高中的线性规划的问题解释。比如线性规划的最优解就应该是这个凸优化问题的解。
下面还要引用知乎的内容:
另外一个问题就是朴素贝叶斯分类器。其主要解决的问题是P(C|D)这个条件概率。C代表类别,D代表文档。其表达的意思是我们要计算在已观测到的文档D判定它属于类别C的概率。由于直接计算这个概率不好计算,贝叶斯的作用就体现出来了。其强大之处就在于可将先验概率与后验概率互相转换。P(C|D)=P(D|C)P(C)/P(D),通过对于样例的训练,我们可以通过bag of words的假设估计出P(D|C),也可以统计出P(C),分母对于所有类别都一样,因此可以忽略。这样,我们就可以把文档D划分到一个概率最大的类C里,就完成了对文档D的分类。
另外研究问题总离不开消费者偏好理论:完备、传递、选择、优势、连续
生产可能性边界如何发挥作用决定生产最佳组合,要与预算线和效用曲线合在一张图上看,三者的切点即是最优点--此时,在一定的预算约束下,A、B的生产替代率等于其价格反比,效用比也等于价格反比,在这一点消费者效用最大化,生产者生产组合最优化。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号