算法导论笔记 第二十八章 矩阵运算

28.1 求解线性方程组

定义

奇异矩阵：秩不是满秩的矩阵

欠定的(线性方程组)：线性方程组的矩阵向量A的秩小于n

超定的(线性方程组)：方程数目超过未知变量的数目n

//其实我早就忘得差不多了=。=赶紧捡起来

LUP分析

找出三个n×n的矩阵L、U和P，满足

PA=LU

//和Program Assignment有啥关系

其中L(lower)是下三角矩阵，U(upper)是上三角矩阵，P是一个置换矩阵。我们称满足上式的矩阵LUP称为A的LUP分解。

对于所有的非奇异矩阵都有这样的分解。在下面的伪代码中转置矩阵由数组π表示。

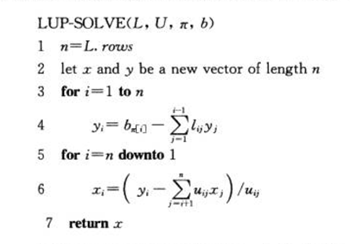
计算一个LU分解

考虑非奇异的n×n矩阵A，采用高斯消元法来创建一个LU分解。

使用递归来化解

这个叫A对于a₁₁的舒尔补（真难听=。=）

在LUP分解中我们所除的元素称为主元，为矩阵U的对角线上，为了避免吧0当做除数，我们在LUP分解中包含一个转置矩阵P，这样的操作叫做选主元。

以下是用迭代代替尾递归的代码：

运行时间为立方级

计算一个LUP分解

和LU分解大同小异

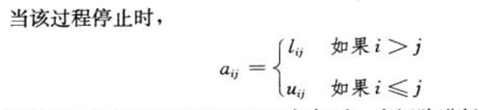
LUP算法概况

1. 第一次取第一列绝对值最大的元素作为主元，并交换到第一行
2. 第一列余下的元素除以这个主元
3. 下一个递归矩阵的元素用自身的值减去对于行列元素排头元素之积
4. 取去掉第一行和第一列的元素为新矩阵，重复以上步骤
5. 分离LU的时候，对于非奇异矩阵，L对角线全部取1，U取原本的
6. LU算法则减少第一步