图论引导笔记 第十章 染色

10.1 四色问题

一个很长很长很长的故事

10.2 顶点染色

定义：

对偶：我们说一个图G是一副地图的对偶，当且仅当(1)G的顶点为地图的区域(2)G的两个顶点是邻接的当且仅当他们对应的区域是相邻的。

真染色（简称染色）：给G的顶点分配一些（来自某个颜色集合的）颜色，每个顶点分配到一种颜色，且邻接的顶点分配到不同的颜色。

色数：在G的所有染色中，使用颜色最少的方案的颜色数。记作χ(G)

K可染色的：能使用含有k种元素颜色的集合给G的顶点染色。（也可以直接理解为色数小于K的图G）

K染色：使用了K种颜色的染色。

（图是）K色的：G是K染色的，满足χ(G)=K

最小染色：图G的每个K染色都是G的最小染色（我怎么感觉最后两个概念换个顺序比较好说）

 

此处回忆一波：独立的，最大独立集，点独立数的概念。

色类：将G.V分成k个独立集{V₁ ，V₂ ，V₃ ，… ，V_k}，但同时不能把G.V分成k-1个独立集，我们称这些顶点集称为色类。

团：图G的一个团指G的一个完全子图。给定无向图G=(V,E)。如果U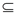V，且对任意u，v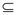U 有(u，v)  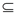E，则称U 是G 的完全子图。

团数：图G中最大团的阶数。记作ω（G）。实际上点独立数β（G）=k当且仅当ω（`G）=k

染色的另一种定义：函数c:V(G)N，使得当uv∈G.E时，c(u)≠c(v)

 

复习：δ(G)最小度，Δ(G)表示最大度

Grotzsch图：一个色数为4且没有三角的图。没错就是下面这个。它的最小完全子图的阶数为2，在10.5中等号取不到。

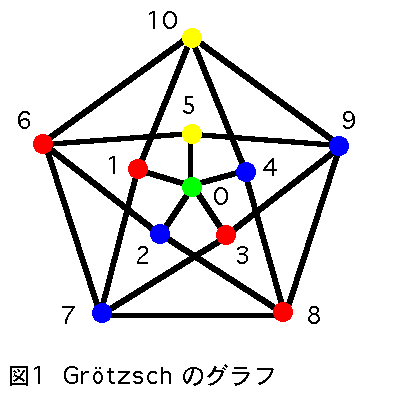
影子图：S（G）是通过对G的每一个顶点v,增加一个新顶点v'，并使得原来在G中的所有顶点v邻接的点都与v'相邻接。得到的图称之为G的影子图。

影子顶点：在上一个定义中提到的v'，即是点v的影子顶点。

性质：（1）影子顶点与原来结点是不相邻接的（2）任意两个影子顶点之间是不相邻接的

 

定理：

10.1四色定理：每个平面图的色数至少为4。

10.2 图G的色数是2，当且仅当G是一个非空二部图。奇圈χ(C_n)=3,偶圈χ(C_n)=2.

10.3 要证明χ(G)=k，需要证明：（1）至少需要k 种颜色给G染色/不能用k-1种颜色给 G染色（2）存在一个G的K染色

10.4 （选课问题）k名学生在n门课集合里面选课，每人可以选几门，排课使得每一个学生的每两节课都不能在同一天的同一个时间段开课

    解：构造一个图H,顶点为这n门课程，两个顶点连一条边如果有某个同学同时选了这两门课，最少时间段数就是χ(G)。

    同时还有结论：若H是G的子图，χ(H)≤χ(G)

10.5对于每个n阶图G, χ(G)≥ω(G)（图的最小染色≥最大完全子图的阶数），χ(G)≥n/β(G) （图的最小染色≥n/点独立数）

    证明：前者：设H是一个阶数为ω(G)的团，对于这个团χ(H)=|H.V|=ω(G)，由于H是G的子图χ(G)≥χ(H)=ω(G)，得证。对于后者，G的独立集的集合元素个数不会超过点独立数，相乘肯定大于n。

10.6 （十字路口交通相位问题）交通灯的相位等于图的色数

10.7 用贪心算法给图的色数一个上界，而色数问题本是NP不可解的。对于每一个G，χ(G)≤1+Δ(G),其中，Δ(G)表示的度最大的点的度数。证明：此时考虑这个点，把该点和其相邻点涂山不同的颜色

    等号取到的一些情况：对于n≥3是奇数，χ(C_n)=1+Δ(C_n)=3显然成立；对于任意完全图χ(K_n)=1+Δ(K_n)=1+（n-1）显然成立。

10.8 (Brook 定理)对每个非奇圈也非完全的连通图G，χ(G)≤Δ(G)

    证明：由于这是一个非完全图，对于最大度顶点k的相邻顶点集adj[k]，此时考虑|adj[k]|≥3的情况（为2阶图（path/tree/circle）的时候单独考虑是都符合的），此时adj[k]必定存在不直接相邻的两个点，取这两个点赋予相同的颜色，其余点赋予不同颜色。命题得证。

10.9 对于每一个图G，χ(G)≤max{δ(H)}+1，其中max遍历取满G的所有诱导子图H

    证明：用一下方法构造一个G所有顶点的序列：在G的所有诱导子图中，设k为max{δ(H)}，假设图G=G_n的阶为n，取其中度数最小的节点为v_n,且v_n ≤k，对于图G_n-1=G-v_n,取其中度数最小的节点v_n-1,同样的有deg v_n-1 ≤k，以此类推得到一个顶点序列v₁, v₂, …, v_n-1, v_n。接下来我们来构建一个图的染色：c(G₁)=1,对于点v_i来说，c(G_i)=max{c(G_i-1),deg v_i+1}。对于任意i,deg v_i≤k，故χ(G)≤max{δ(H)}+1成立。原命题得证。

10.10 对于每一个整数k≥3，都存在一个色数为k的无三角的图。

    证明：【构造证明与归纳证明】对于k=3,4的情况是成立的，对于一个无三角的(k-1)色图G，我们在他的影子图S(G)中增加一个新结点u，使得u与每一个影子结点相连，得到的新图H是k色无三角的图。先反证法证明没有三角，然后把原来图扩成加一色的图。证毕。