叉积

向量基本运算

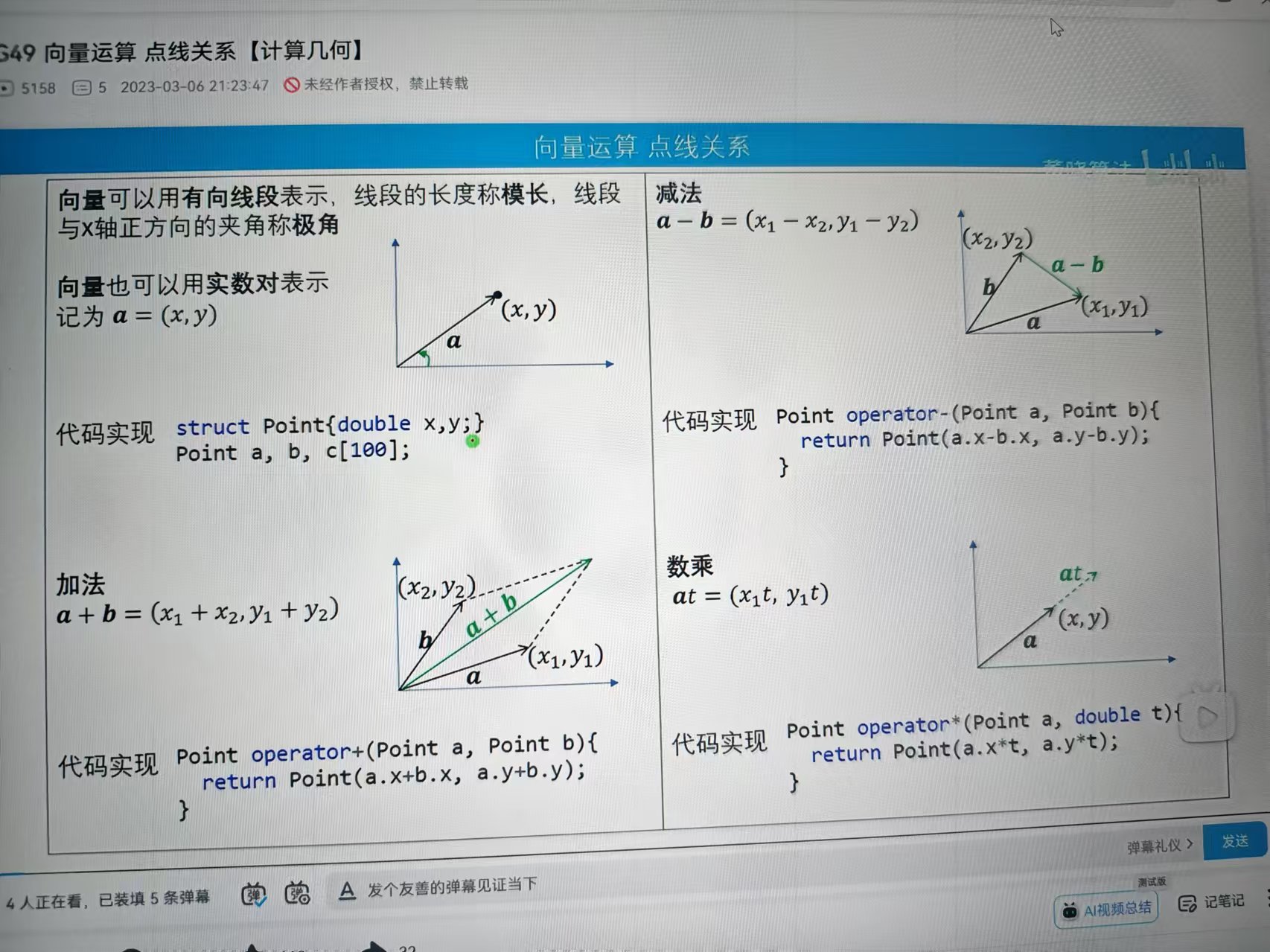
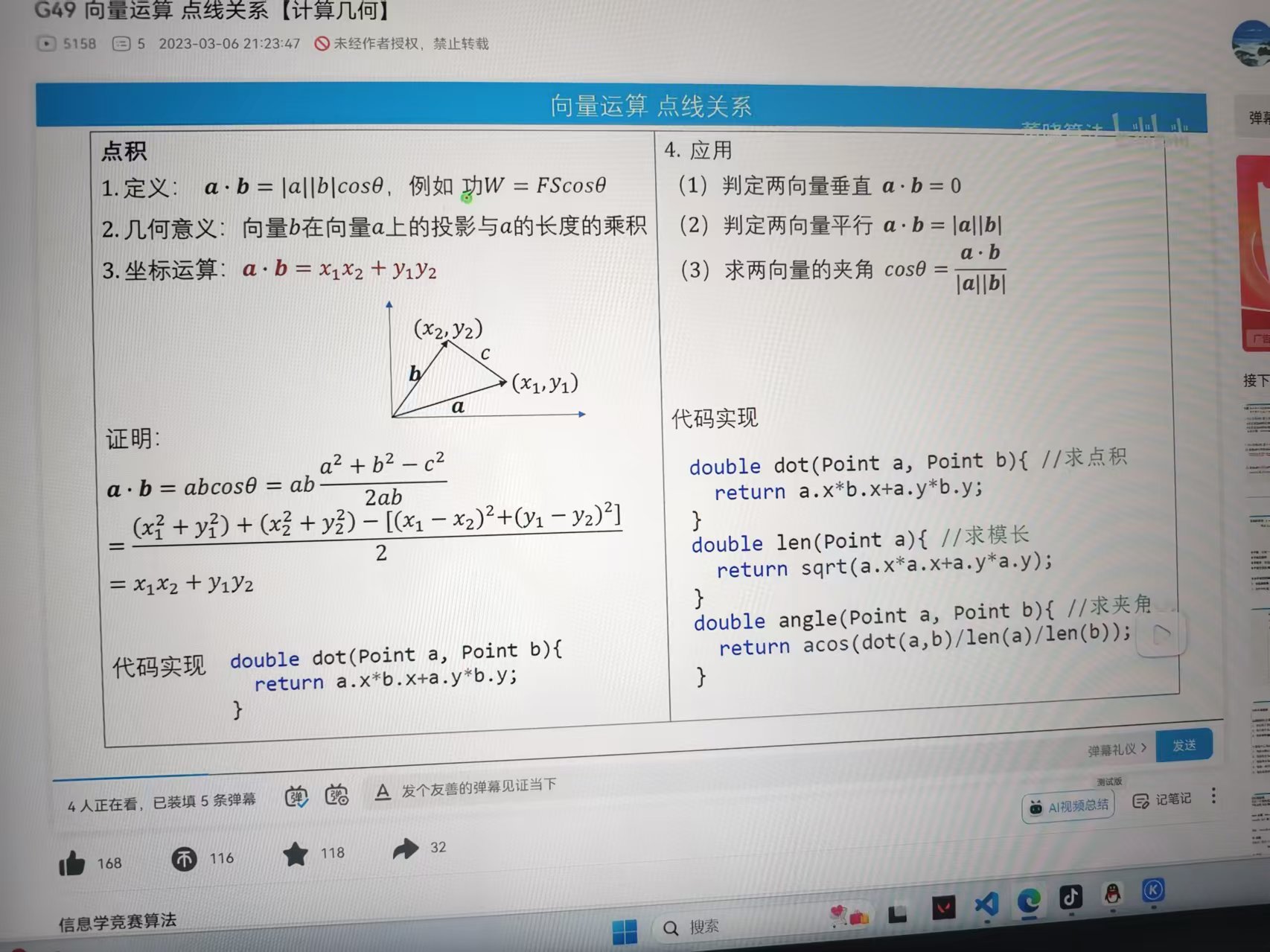
点积

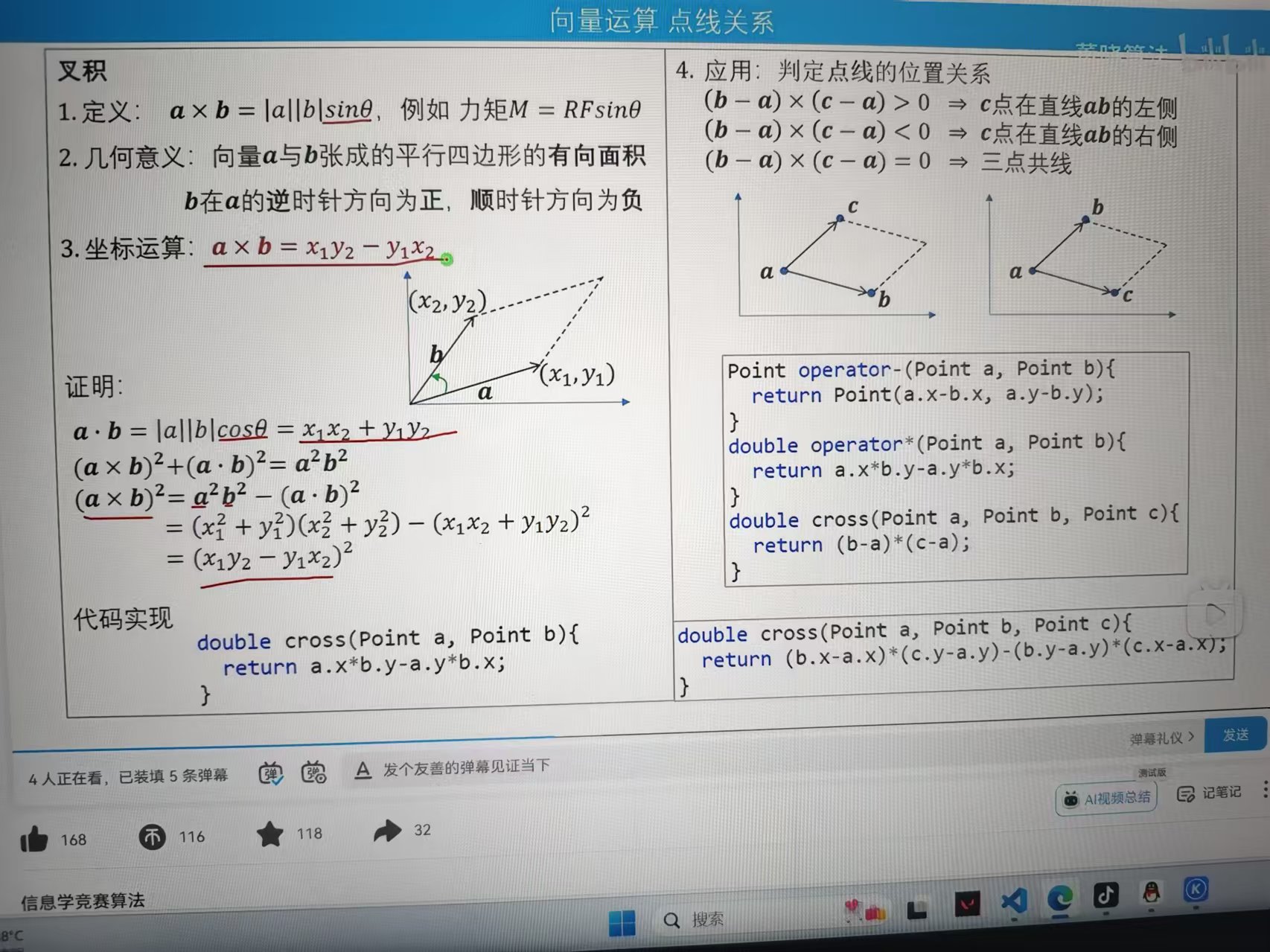
叉积

一.Transmitters

由叉积的基本定理得出，要判断一个点c再一条直线ab的左边还是右边，只要看（b-a）*（c-a）大于0还是小于0，对于这题，我们可以将左右边看成发射范围的半圆，因为要找出覆盖最多点的数量，所以最优解肯定有一个点再直径上，再通过叉积找出所有在这个点左侧的点。并且在初始化的时候，如果发现一个点到圆心的距离大于圆的半径，那这个点就不用考虑了。

点击查看代码

#include <iostream>  // 输入输出流
#include <iomanip>   // 输入输出格式控制
#include <fstream>   // 文件输入输出流
#include <sstream>   // 字符串输入输出流
#include <cmath>     // 数学函数
#include <string>    // 字符串操作
#include <vector>    // 动态数组容器
#include <queue>     // 队列容器
#include <stack>     // 栈容器
#include <set>       // 集合容器
#include <map>       // 映射容器
#include <algorithm> // 算法
#include <bitset>    // 位集容器
#include <stdio.h>   // 标准输入输出
using namespace std;
#define int long long
const int N = 1e6 + 5, M = 1e6 + 5;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f3f3f3f3f;
double a[N], b[N];
double x, y, r;
double dis(double xx, double yy) // 计算距离
{
    return sqrt(1.0 * (x - xx) * (x - xx) + (y - yy) * (y - yy));
}
double cha(double xx, double yy, double xxx, double yyy) // 计算叉积
{
    return (xx - x) * (yyy - y) - (xxx - x) * (yy - y);
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    while (cin >> x >> y >> r, r >= 0)
    {
        int n;
        cin >> n;
        int cnt = 0;
        for (int i = 1; i <= n; i++)
        {
            int xx, yy;
            cin >> xx >> yy;
            if (dis(xx, yy) <= r) // 将点到圆心距离小于r的点放入
            {
                a[++cnt] = xx;
                b[cnt] = yy;
            }
        }
        int max1 = 0;
        for (int i = 1; i <= cnt; i++) // 枚举每一个点在半圆的直径上，计算其左侧的点
        {
            int s = 0;
            for (int j = 1; j <= cnt; j++)
            {
                if (cha(a[i], b[i], a[j], b[j]) >= 0) // 如果叉积大于0，说明在左侧，等于0，则在直径上，都符合条件
                {
                    s++;
                }
            }
            max1 = max(max1, s); // 记录最大的左侧点数
        }
        cout << max1 << "\n";
    }

    return 0;
}

二.TOYS

将一个纸板分成了n+1个部分，因为每个分割点的坐标x是递减的，所以可以想到二分，而每个部分则是由分割线右边的那块地方包含的，所以要判断每个点落在哪个部分，就是不断二分判断对于那个部分，点和分割线的叉积是否小于0。

点击查看代码

#include <iostream>  // 输入输出流
#include <iomanip>   // 输入输出格式控制
#include <fstream>   // 文件输入输出流
#include <sstream>   // 字符串输入输出流
#include <cmath>     // 数学函数
#include <string>    // 字符串操作
#include <vector>    // 动态数组容器
#include <queue>     // 队列容器
#include <stack>     // 栈容器
#include <set>       // 集合容器
#include <map>       // 映射容器
#include <algorithm> // 算法
#include <bitset>    // 位集容器
#include <stdio.h>   // 标准输入输出
#include <cstring>
using namespace std;
const int N = 100010, M = 20;
#define int long long
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f3f3f3f3f;
int x, y, n, m, x1, y3;
struct vv
{
    int x, y;
} a[N], b[N], p;
int cha(int mid)
{
    return ((a[mid].x - b[mid].x) * (p.y - b[mid].y)) - (a[mid].y - b[mid].y) * (p.x - b[mid].x);
}
int s[N];
int find() // 二分查找对于每个部分的叉积是否小于0
{
    int l = 1, r = n + 1;
    while (l <= r)
    {
        int mid = (l + r + 1) / 2;
        if (cha(mid) <= 0)
        {
            l = mid + 1;
        }
        else
        {
            r = mid - 1;
        }
    }
    return r;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    while (cin >> n, n)
    {
        cin >> m >> x >> y >> x1 >> y3;
        int cnt = 1;
        a[1].x = x, a[1].y = y, b[1].x = x, b[1].y = y3; // 先将盒子的起点的两端点记录数组
        for (int i = 2; i <= n + 1; i++)
        {
            int l, r;
            cin >> l >> r;
            a[i].x = l;
            a[i].y = y;
            b[i].x = r;
            b[i].y = y3;
        }
        memset(s, 0, sizeof(s));
        while (m--) // 对于每个玩具，find找出其所在的部分，然后加1，找出最大值。
        {
            cin >> p.x >> p.y;
            s[find()]++;
        }
        for (int i = 1; i <= n + 1; i++)
        {
            cout << i - 1 << ": " << s[i] << endl;
        }
        cout << "\n";
    }
    return 0;
}