虚树学习笔记
虽说 NOIP 不考这玩意儿,但作为一名 OIer 早学晚学都得要学,所以今天花了一晚上时间搞清楚这是怎么一回事了。
其实是因为模拟赛考了道虚树
拿道题来举个例子吧,洛谷 P2495 [SDOI2011]消耗战
题意:给出一个 \(n\) 个点的树,边上有边权,\(m\) 组询问,每次询问给出 \(k\) 个点 \(x_1,x_2,x_3,\dots,x_k\)。现在你要割掉一些边使得这 \(k\) 个点都不能到达 \(1\) 号点,问割掉的边的边权和的最小值是多少。\(\sum k\leq 5\times 10^5\)。
考虑朴素的 \(dp\)。令 \(dp_x\) 表示 \(x\) 子树内的节点全部割掉的最小代价。转移的时候枚举子节点 \(y\):
- 如果 \(y\) 不是关键点,那么要么把 \(x\) 与 \(y\) 之间的边割掉,要么把 \(y\) 子树内的点都割掉。
- 如果 \(y\) 是关键点,那么只能把 \(x\) 与 \(y\) 之间的边割掉。
由此可以写出状态转移方程 \(dp_x=\sum\limits_{(y,z)\in son_x}\min(z,dp_y)\)。
不过这样很明显是不行的,每次询问都需遍历整棵树,总复杂度 \(\mathcal O(nm)\)。
注意到虽然总点数很多,但是有个条件 \(\sum k\leq 5\times 10^5\),说明有用的点数并不多。
这就启发我们,是否能够将原树缩小为一棵与原树形态类似的、包含所有有用点的树呢?
这时我们就要用到虚树
所谓虚树,就是包含 \(k\) 个关键点及其 LCA 的树,将原树不重要的节点之间的链简化成单条边或删去。
那么,怎样构建虚树呢?先求出原树的 dfs 序。
我们维护一条从根节点出发的链,栈顶存这条链中深度最深的节点,栈底存深度最浅的节点。
注意,这些节点都是关键节点。
按照 dfs 序从小到大的顺序依次插入这 \(k\) 个关键点。
设栈顶到栈底的元素分别是 \(stk[1],stk[2],\dots,stk[tp]\)
假设插入节点 \(x\),设 \(lc=LCA(x,stk[tp])\)。
接下来就到了愉快的分类讨论时间了:
- 若 \(lc=stk[tp]\),即 \(x\) 在 \(stk[tp]\) 的子树中,那么直接把它插到队列尾就可以了。
- 若 \(dep[lc]>dep[stk[tp-1]]\),也就是 \(lc\) 介于 \(stk[tp]\) 和 \(stk[tp-1]\) 之间,由于我们是按 \(dfs\) 序插入的,接下来就不会有 \(lc\) 和 \(stk[tp]\) 之间的节点了,就在 \(lc\) 与 \(stk[tp]\) 之间连边,并将 \(stk[tp]\) 弹出,插入 \(lc\) 和 \(x\)。
- 若 \(lc=stk[tp-1]\),与上一种情况类似,唯一不同的是不用插入 \(lc\) 了。
- 若 \(dep[lc]<dep[stk[tp-1]]\),也就是说 \(lc\) 在 \(stk[tp-1]\) 之前,那么就不断弹出栈顶直到满足条件 2 或条件 3.
代码大概长这样:
inline void insert(int x){
if(!tp){stk[++tp]=x;return;}//if there are no element in the stack, just push node x and return
int lc=graph::getlca(x,stk[tp]);//find the lca of the newly-added node and the top of the stack
while(tp>=2&&dep[lc]<dep[stk[tp-1]]){//pop the stack until one of condition 1,2,3 holds (condition 4)
adde(stk[tp-1],stk[tp]);tp--;//add the edge between adjacent nodes
}
if(tp&&dep[lc]<dep[stk[tp]]) adde(lc,stk[tp--]);//if lc is between stk[tp-1] and stk[tp], add an edge between lc and stk[top] (condition 2,3)
if(!tp||lc!=stk[tp]) stk[++tp]=lc;//condition 2
stk[++tp]=x;//push node x
}
注意,到了最后,仍然留在栈里的元素之间是没有连边的,因此插入完每个节点之后应当进行收尾操作。
inline void fin(){
while(tp>=2) adde(stk[tp-1],stk[tp]),tp--;
stk[tp--]=0;
}
建好树以后,直接在虚树上跑上面的 dp 就可以了。
最后,可能还会有一些疑问,这里统一解答:
- 为什么在条件 4 中 \(stk[tp],stk[tp-1],\dots\) 可以直接弹出栈?
因为你是按照 dfs 序依次插入的,所以在它下面的点一定会被先访问,也就是说当你插入 \(x\) 的时候它下面的点已经被访问过了,因此 \(stk[tp],stk[tp-1],\dots\) 在以后的操作中就没用了。 - 该算法时间复杂度是多少?
所有关键点入栈出栈各一次,瓶颈在于排序上,\(\mathcal O(k \log k)\) - 怎样清空虚树?
暴力清空复杂度还是会达到 \(\mathcal O(n)\),所以要清空虚树,应进行一遍 dfs,每次遍历完一个节点的子树后,将其邻接表清空,切记不要 memset 一遍了事。
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define mp make_pair
#define int long long
typedef pair<int,int> pii;
int n,m;
namespace graph{
vector<pii> g[500005];
int fa[500005][22],dfn[500005],dep[500005],tim=0;
int dist[500005][22];
inline void dfs(int x,int f){
fa[x][0]=f;dfn[x]=++tim;
for(int i=0;i<g[x].size();i++){
int y=g[x][i].fi,z=g[x][i].se;
if(y==f) continue;
dep[y]=dep[x]+1;dist[y][0]=z;
dfs(y,x);
}
}
inline int getlca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=18;~i;i--) if(dep[x]-(1<<i)>=dep[y]) x=fa[x][i];
if(x==y) return x;
for(int i=18;~i;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
inline int getdis(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
int mn=0x3f3f3f3f3f3f3f3fll;
for(int i=20;~i;i--) if(dep[x]-(1<<i)>=dep[y]) mn=min(mn,dist[x][i]),x=fa[x][i];
if(x==y) return mn;
for(int i=20;~i;i--) if(fa[x][i]!=fa[y][i]) mn=min(mn,min(dist[x][i],dist[y][i])),x=fa[x][i],y=fa[y][i];
mn=min(mn,dist[x][0]);mn=min(mn,dist[y][0]);
}
inline void prework(){
dfs(1,0);
for(int i=1;i<=20;i++) for(int j=1;j<=n;j++){
fa[j][i]=fa[fa[j][i-1]][i-1];
dist[j][i]=min(dist[j][i-1],dist[fa[j][i-1]][i-1]);
}
}
}
using graph::dep;
using graph::dfn;
namespace virt{
vector<pii> g[500005];
bool cmp(int x,int y){
return dfn[x]<dfn[y];
}
inline void adde(int x,int y){
// printf("adde %d %d\n",x,y);
g[x].pb(mp(y,graph::getdis(x,y)));
}
int stk[500005],tp=0;
inline void insert(int x){
if(!tp){stk[++tp]=x;return;}
int lc=graph::getlca(x,stk[tp]);
while(tp>=2&&dep[lc]<dep[stk[tp-1]]){
adde(stk[tp-1],stk[tp]);tp--;
}
if(tp&&dep[lc]<dep[stk[tp]]) adde(lc,stk[tp--]);
if(!tp||lc!=stk[tp]) stk[++tp]=lc;
stk[++tp]=x;
}
inline void fin(){
while(tp>=2) adde(stk[tp-1],stk[tp]),tp--;
stk[tp--]=0;
}
int poi[500005];
bool mark[500005];
int dp[500005];
inline void dfs(int x){
if(mark[x]) return;
for(int i=0;i<g[x].size();i++){
int y=g[x][i].fi,z=g[x][i].se;dfs(y);
if(mark[y]) dp[x]+=z;
else dp[x]+=min(dp[y],z);
}
}
inline void clear(int x){
mark[x]=dp[x]=0;
for(int i=0;i<g[x].size();i++){
int y=g[x][i].fi,z=g[x][i].se;
clear(y);
}
while(g[x].size()) g[x].pop_back();
}
inline void solve(){
int k;scanf("%d",&k);
for(int i=1;i<=k;i++) scanf("%d",&poi[i]);
sort(poi+1,poi+k+1,cmp);stk[++tp]=1;
for(int i=1;i<=k;i++) mark[poi[i]]=1;
for(int i=1;i<=k;i++) insert(poi[i]);
fin();dfs(1);
printf("%lld\n",dp[1]);
clear(1);
}
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<n;i++){
int u,v,w;scanf("%lld%lld%lld",&u,&v,&w);
graph::g[u].pb(mp(v,w));
graph::g[v].pb(mp(u,w));
}
scanf("%lld",&m);
graph::prework();
while(m--) virt::solve();
return 0;
}
upd on 2020.12.28:
CSP 之前学的,大概已经 2 个月了吧,我真是个鸽子(大雾
下面是一些其他例题:
CF613D Kingdom and its Cities
老套路,看到 \(\sum k_i\leq 10^5\) 就建出虚树。
显然如果出现父子俩都被选中就直接 \(-1\) 了。
设 \(f_i\) 为以 \(i\) 为根的子树的答案。
再设一个 \(hav_i\) 表示在以 \(i\) 为根的子树内,是否存在某个关键点与 \(i\) 连通。
分 \(i\) 为关键点和 \(i\) 不是关键点转移。
如果 \(i\) 为关键点,那么对于 \(i\) 的所有儿子 \(v\),首先肯定会有一个 \(f_v\) 的代价,其次如果 \(hav_v=1\),就意味着存在某个关键点与 \(v\) 连通,此时就必须把 \(v\) 堵住。故 \(f_i=\sum\limits_{(i,v)}f_v+hav_v\),而关键点 \(i\) 肯定与自己连通,故 \(hav_i=1\)。
如果 \(i\) 不是关键点,还是枚举 \(i\) 的儿子 \(v\),还是肯定会有一个 \(f_v\) 的代价。假设 \(cnt\) 为 \(hav_v=1\) 的 \(v\) 的个数。
分类讨论:
- 如果 \(cnt\geq 2\),那么这个点必须堵上,直接令 \(f_i\) 加 \(1\)。
- 如果 \(cnt=1\),那么我们肯定是选择到某个祖先的位置再堵上,\(hav_i=1\)
- 如果 \(cnt=0\),那么就没有与 \(i\) 相连通的关键点 \(hav_i=0\)。
时间复杂度 \(k\log k\)。
洛谷 P4103 [HEOI2014]大工程
建出虚树,虚树上的边权为原树中两点间路径的长度。
第一问,直接计算每条边产生的贡献,把它们累加起来即可,一条边 \((x,y)\) 的被计算的次数即为 \(sz_y\times(k-sz_y)\)。
第二问第三问,设 \(mnf_u,mns_u\) 为以 \(u\) 为一端,\(u\) 子树内的某个关键点 \(v\) 为另一端的链中,边权最小的、次小的链,\(mxf_u,mxs_u\) 为以 \(u\) 为一端,\(u\) 子树内的某个关键点 \(v\) 为另一端的链中,边权最大的、次大的链。按照树的直径的方式转移即可。最终第二问答案即为 \(\min mnf_u+mns_u\),第三问答案即为 \(\max mxf_u+mxs_u\)。
洛谷 P3233 HNOI2014]世界树
虚树的关键不在于你看出它是虚树,而是建完虚树之后怎么搞
看到 \(\sum m_i\leq 10^5\),果断建出虚树。
然后就不是太会做了/kk
首先本题要计算整棵树中的答案,所以我们尝试把答案拆成 2 部分:
-
虚树上的点对答案的贡献
记 \(by_x\) 离 \(x\) 最近的点的编号。\(by_x\) 显然可以通过两遍 dfs 求出(第一遍 dfs 求出 \(x\) 子树内的贡献,用儿子更新父亲,第二遍 dfs 求出 \(x\) 子树外的贡献,用父亲更新儿子,类似于换根 dp),然后令所有 \(by_x\) 加 \(1\) 即可。
-
不在虚树上的点对答案的贡献
这一部分比较复杂,我们不妨画个图来帮助我们理解。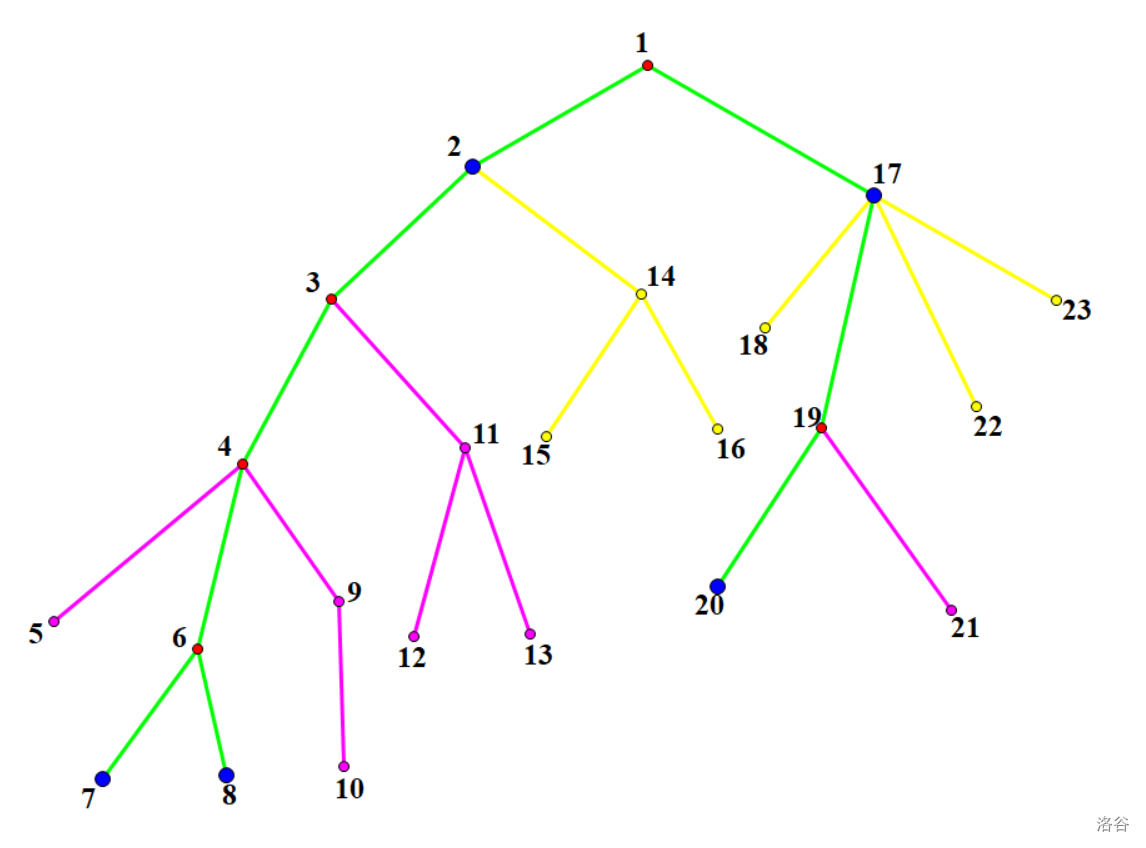
如图,蓝色节点为关键点,绿色的边为虚树组成的边。显然,除了节点 \(1,2,6,7,8,17,20\) 之外其它节点都不在虚树上。
我们又可把这些节点分为两类:
Ⅰ. 虚树上某个节点的儿子的子树(即图中的黄色节点)。假设我们考虑关键节点 \(u\) 这部分的贡献,那么这个贡献显然可以表示为 \(sz_u-1-\sum\limits_{v\in son_u}sz_v\),也就是整个 \(u\) 子树的大小扣掉在虚树上的儿子的子树大小。但是这里我们不能直接枚举虚树上的儿子。比方说我们要计算节点 \(2\) 那部分黄色子树的贡献。节点 \(2\) 在虚树上的唯一儿子为节点 \(6\)。而直接拿 \(sz_2-1-sz_6\) 显然是不行的,正确的结果应该是 \(sz_2-1-sz_3\)。故这里我们要减去 \(u\) 在 \(v\) 方向的直接儿子。那么这个直接儿子怎么求呢?借鉴 CF916E 的套路,求出 \(v\) 的 \(dep_v-dep_u-1\) 级祖先就行了。
Ⅱ. 虚树上某两个节点 \(u,v\) 之间的点及其子树内的节点,(即图中的粉色节点)
继续分情况:
①. \(by_u=by_v\),那么显然 \(u,v\) 所有节点都属于 \(by_v\)。找出 \(u\) 在 \(v\) 方向的直接儿子 \(s\),并令 \(sz_{by_u}\) 加上 \(sz_s-sz_v\)
②. \(by_u\neq by_v\),显然 \(by_u\) 与 \(by_v\) 分别位于边 \((u,v)\) 的两侧。画张比较清晰的图:
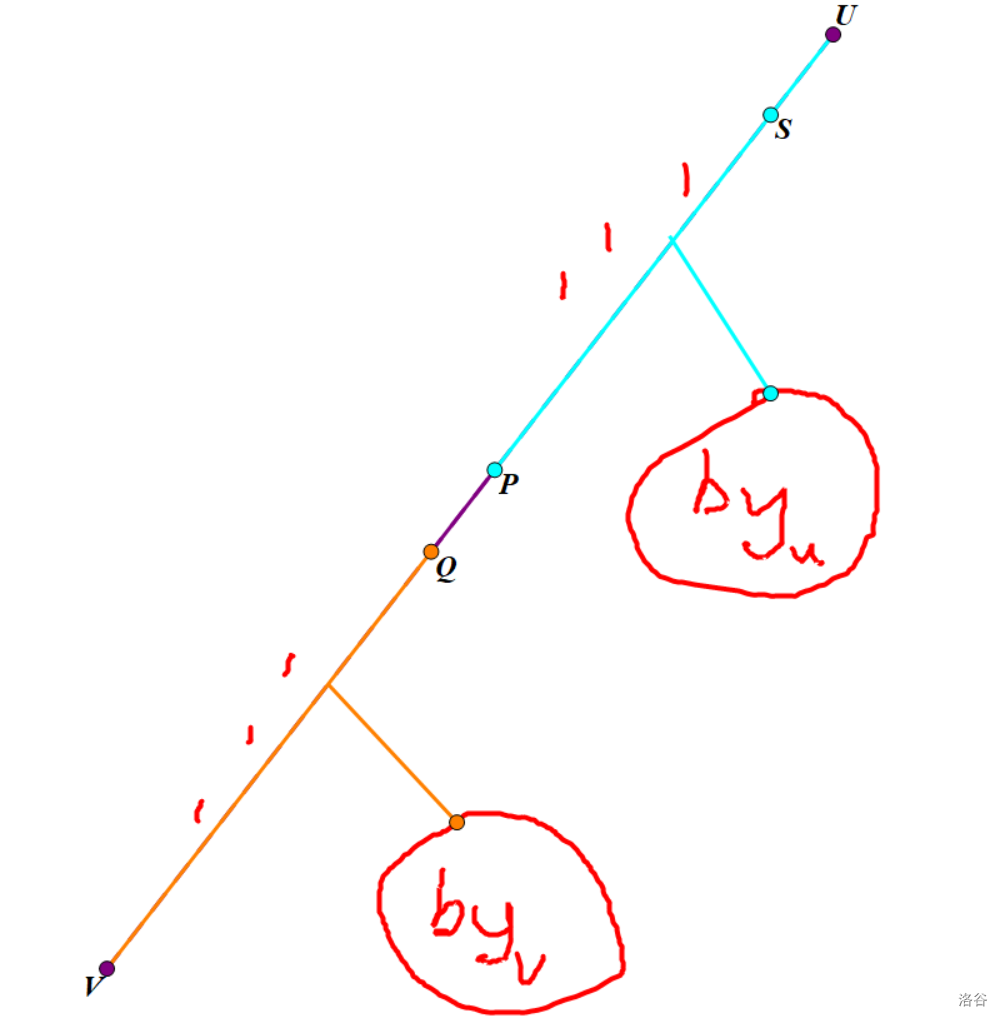
二分枚举断点 \(p,q\),\(p\) 及上面部分都属于 \(by_u\),\(q\) 及下面部分都属于 \(by_v\)。那么这条路径上的点对 \(by_u\) 贡献就是 \(sz_s-sz_q\),对 \(by_v\) 的贡献就是 \(sz_q-sz_v\)。
真是道恶心的题啊
CF639F Bear and Chemistry
然而上一题还不是最恶心的。因为这题比上题还恶心。
本篇开头”其实是因为模拟赛考了道虚树“说的就是此题。
u1s1 出题人你确定有人 4h 能肝出这题?
看到”不经过重复的边“,立刻想到边双连通分量。显然集合 \(S\) 中的点满足条件当且仅当它们全在同一个边双中。
于是这题思路就有了:先将原图边双缩个点,缩成一棵森林。然后对每组询问建虚树,再跑一遍边双,判断 \(S\) 中的点是否全在一个边双里就行了。
是不是异常简单?然而听听就 haipa。
本题实现起来有不少坑点:
- 本题是一棵森林,所以建虚树的时候还要考虑 \(lc\) 为 \(0\) 的情况——直接清空栈就行了。
- 本题的清空非常恶心,直接一遍 dfs 不好清空,需建一个 vector 储存本次询问中用到了哪些点,然后清空最后对 vector 中的点的对应数据。
- 感觉本题强制在线说的不是太清楚 qwq,一开始把题目中 \(R\) 的定义看成 YES 的个数,实际上应该是所有答案为 YES 的询问编号之和。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=3e5;
const int LOG_N=19;
int n,m,qu,k;
struct graph{
int hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=1;
graph(){memset(hd,0,sizeof(hd));memset(to,0,sizeof(to));memset(nxt,0,sizeof(nxt));ec=1;}
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
} g0,t,im;
namespace ecc{
int dfn[MAXN+5],low[MAXN+5],tim=0;stack<int> stk;
int from[MAXN+5];bitset<MAXN*2+5> bri;
void tarjan(int x,int f){
dfn[x]=low[x]=++tim;stk.push(x);
for(int e=g0.hd[x];e;e=g0.nxt[e]){
int y=g0.to[e];
if(!dfn[y]){
tarjan(y,x);low[x]=min(low[x],low[y]);
if(low[y]>dfn[x]) bri[e]=bri[e^1]=1;
} else if(y!=f) low[x]=min(low[x],dfn[y]);
}
}
void dfs(int x){
if(from[x]) return;from[x]=k;
for(int e=g0.hd[x];e;e=g0.nxt[e]){
int y=g0.to[e];if(!bri[e]) dfs(y);
}
}
void work(){
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
for(int i=1;i<=n;i++) if(!from[i]) k++,dfs(i);
// for(int i=1;i<=n;i++) printf("%d\n",from[i]);
for(int x=1;x<=n;x++) for(int e=g0.hd[x];e;e=g0.nxt[e]){
int y=g0.to[e];if(from[x]!=from[y]) t.adde(from[x],from[y]);
}
}
}
int fa[MAXN+5][LOG_N+2],dfn[MAXN+5],tim=0,dep[MAXN+5];
void dfs(int x,int f){
fa[x][0]=f;dfn[x]=++tim;
for(int e=t.hd[x];e;e=t.nxt[e]){
int y=t.to[e];if(y==f) continue;
// printf("%d %d\n",x,y);
dep[y]=dep[x]+1;dfs(y,x);
}
}
int getlca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=LOG_N;~i;i--) if(dep[x]-(1<<i)>=dep[y]) x=fa[x][i];
if(x==y) return x;
for(int i=LOG_N;~i;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
ll R=0;
int rotate(int element){
element=(element+R)%n;
if(element==0) element=n;
return element;
}
namespace virt{
bool cmp(int x,int y){return dfn[x]<dfn[y];}
int vn,en,pt[MAXN*3+5],pn,comp=0;
int eu[MAXN+5],ev[MAXN+5],ex[MAXN+5];
int stk[MAXN+5],tp=0;
bool used[MAXN+5];vector<int> vs;
void adde(int u,int v){im.adde(u,v);im.adde(v,u);}
void addnode(int x){if(!used[x]) used[x]=1,vs.pb(x);}
void insert(int x){
addnode(x);
if(!tp){stk[++tp]=x;return;}
int lc=getlca(stk[tp],x);
// printf("ins %d %d\n",x,lc);
if(!lc){while(tp>=2) adde(stk[tp],stk[tp-1]),tp--;stk[tp--]=0;stk[++tp]=x;return;}
addnode(lc);
while(tp>=2&&dep[stk[tp-1]]>dep[lc]) adde(stk[tp],stk[tp-1]),tp--;
if(tp&&dep[stk[tp]]>dep[lc]) adde(stk[tp],lc),tp--;
if(!tp||lc!=stk[tp]) stk[++tp]=lc;stk[++tp]=x;
}
void fin(){while(tp>=2) im.adde(stk[tp-1],stk[tp]),im.adde(stk[tp],stk[tp-1]),tp--;stk[tp--]=0;}
void build(){
sort(pt+1,pt+pn+1,cmp);pn=unique(pt+1,pt+pn+1)-pt-1;
// for(int i=1;i<=pn;i++) used[pt[i]]=1,vs.pb(pt[i]);
// for(int i=1;i<=pn;i++) printf("insert %d\n",pt[i]);
for(int i=1;i<=pn;i++) insert(pt[i]);fin();
}
int _dfn[MAXN+5],_low[MAXN+5],_tim=0;stack<int> _stk;
int _from[MAXN+5];bitset<MAXN*2+5> _bri;
void tarjan(int x,int f){
_dfn[x]=_low[x]=++tim;_stk.push(x);
for(int e=im.hd[x];e;e=im.nxt[e]){
int y=im.to[e];
if(!_dfn[y]){
tarjan(y,x);_low[x]=min(_low[x],_low[y]);
if(_low[y]>_dfn[x]) _bri[e]=_bri[e^1]=1;
} else if(y!=f) _low[x]=min(_low[x],_dfn[y]);
}
}
void dfs(int x){
if(_from[x]) return;_from[x]=comp;
for(int e=im.hd[x];e;e=im.nxt[e]){
int y=im.to[e];if(!_bri[e]) dfs(y);
}
}
void findecc(){
ffe(it,vs) if(!_dfn[*it]) tarjan(*it,0);
ffe(it,vs) if(!_from[*it]) comp++,dfs(*it);
}
void clear(){
// fill0(ex);fill0(eu);fill0(ev);_bri.reset();fill0(_dfn);fill0(_low);fill0(_from);fill0(used);fill0(im.hd);
// fill0(im.nxt);fill0(im.to);fill0(pt);while(_stk.size()) _stk.pop();fill0(stk);tp=0;
for(int i=1;i<=vn;i++) ex[i]=0;
for(int i=1;i<=en;i++) eu[i]=ev[i]=0;
for(int i=1;i<=im.ec;i++) _bri[i]=0;
// ffe(it,vs) printf("%d\n",*it);
ffe(it,vs) _dfn[*it]=_low[*it]=_from[*it]=used[*it]=im.hd[*it]=0;
vs.clear();im.ec=1;_tim=comp=0;
int cur=1;while(pt[cur]) pt[cur++]=0;pn=0;
}
void work(int id){
scanf("%d%d",&vn,&en);
for(int i=1;i<=vn;i++){
scanf("%d",&ex[i]);ex[i]=rotate(ex[i]);
// printf("real %d\n",ex[i]);
ex[i]=ecc::from[ex[i]];pt[++pn]=ex[i];
}
// for(int i=1;i<=vn;i++) printf("%d\n",ex[i]);
for(int i=1;i<=en;i++){
scanf("%d%d",&eu[i],&ev[i]);
eu[i]=rotate(eu[i]);ev[i]=rotate(ev[i]);
// printf("real %d %d\n",eu[i],ev[i]);
eu[i]=ecc::from[eu[i]];ev[i]=ecc::from[ev[i]];
pt[++pn]=eu[i],pt[++pn]=ev[i];
} build();
// for(int i=1;i<=en;i++) printf("%d %d\n",eu[i],ev[i]);
for(int i=1;i<=en;i++) im.adde(eu[i],ev[i]),im.adde(ev[i],eu[i]);
findecc();bool flg=1;for(int i=1;i<=vn;i++) flg&=(_from[ex[i]]==_from[ex[1]]);
if(flg) R+=id,puts("YES");else puts("NO");
clear();
}
}
int main(){
scanf("%d%d%d",&n,&m,&qu);
for(int i=1;i<=m;i++){
int u,v;scanf("%d%d",&u,&v);
g0.adde(u,v);g0.adde(v,u);
} ecc::work();
for(int i=1;i<=k;i++) if(!fa[i][0]) dfs(i,0);
for(int i=1;i<=LOG_N;i++) for(int j=1;j<=k;j++) fa[j][i]=fa[fa[j][i-1]][i-1];
for(int _=1;_<=qu;_++) virt::work(_);
return 0;
}
/*
15 14 1
1 2
2 3
2 4
4 5
4 6
6 7
6 8
8 9
8 10
10 11
11 12
12 13
13 14
13 15
4 7
1 15 14 3
1 3
2 5
4 7
6 9
8 11
10 13
14 15
*/
洛谷 P4606 [SDOI2018]战略游戏
巧了这题用到的知识点在 3 天内都学过。
本题等价于求:有多少个点为 \(S\) 其中某两点路径上的必经之点。
建出圆方树,那么 \(u,v\) 路径上所有圆点都是 \(u,v\) 路径上的必经之点。
对 \(S\) 中的点建虚树,那么答案就是虚树中的关键点及关键点与关键点边上圆点个数。
实际上这题连虚树都不用建出来,直接用那道 Colorful Tree 的套路,将所有点按 dfs 序排序,计算相邻两点之间路径(扣除掉它们 LCA)上的贡献之和。这样除了所有点的 LCA 之外每个点都被算了 2 次,故将这个和除以 \(2\),如果所有点的 LCA 是个圆点就令答案 \(+1\)。最后扣除掉已经被占领了的 \(|S|\) 个点的贡献即可。
CF1320E Treeland and Viruses
建虚树的部分就不多说了。
考虑点 \(u_i\) 会被怎么样的病毒覆盖。对于一种病毒 \(j\),病毒 \(j\) 覆盖城市 \(i\) 需要 \(\lceil\frac{dis(u_i,v_j)}{s_j}\rceil\) 天。
那么覆盖城市 \(u_i\) 的病毒就应当是 \(\lfloor\frac{dis(u_i,v_j)}{s_j}\rfloor\) 最小的 \(j\)。如有多个这样的 \(j\) 取编号最小的 \(j\)。也就是 \((\lceil\frac{dis(u_i,v_j)}{s_j}\rceil,j)\) 最小的 \(j\)。
把 \((\lceil\frac{dis(u_i,v_j)}{s_j}\rceil,j)\) 当作距离值压在 priority_queue 里,然后跑多源最短路就行了。
另外多说一句,虚树最容易犯的错误就是回答完询问之后忘清空,或者没有清空全部数组。我因此一直 TLE 7,调了 1h,吐血
LOJ 6184 无心行挽
这题我从去年调到了今年。
感觉跟 P3233 世界树差不多吧,可能比 P3233 稍微烦一些。
两遍 dfs 预处理出虚树上每个点离哪个关键点最近。还是分两种情况:
- 在虚树上的点对答案的贡献,直接用 \(dist(x,by_x)\) 更新答案即可。
- 不在虚树上的点对答案的贡献
按照 P3233 的套路这种情况又可分为两种情况:
Ⅰ. 在以虚树上某个点为根的子树中,即图中的橙色部分。

考虑橙色部分中的某个点 \(u\),从 \(u\) 走到离它最近的关键点肯定是先从 \(u\) 走到 \(x\),再从 \(x\) 走到 \(by_x\),经过的路径长为 \(dep_u-dep_x+dist(x,by_x)\)。故我们只需找到橙色部分中深度最深的点即可。那么这个深度最深的点是什么呢?设 \(mxdep_x=x\) 子树中深度最深的点,故这个最大值就是扣除所有在虚树中的儿子 \(v\) 所在的子树后,剩余部分的节点中,深度最大的点。考虑对每个点 \(x\) 建一个 std::multiset 维护 \(x\) 所有儿子的 \(mxdep\) 值。每次遍历到一个节点的时候,就枚举 \(v\in son_u\),然后将 \(u\) 在 \(v\) 方向上的直接儿子 \(s\) 的 \(mxdep\) 值从 std::multiset 删除就可以了。
Ⅱ. 在虚树上某条边上的节点或其子树内的节点
继续分情况:
①. \(by_u=by_v\),这意味着这条路径上所有点 \(x\) 都会对 \(by_u\) 产生贡献,但是这个贡献究竟怎么算呢?
发现没法直观地算出 \(dist(x,by_u)\),所以进而又要分情况:
①.1 \(by_u,by_v\) 均在 \(u\) 上方的子树中。
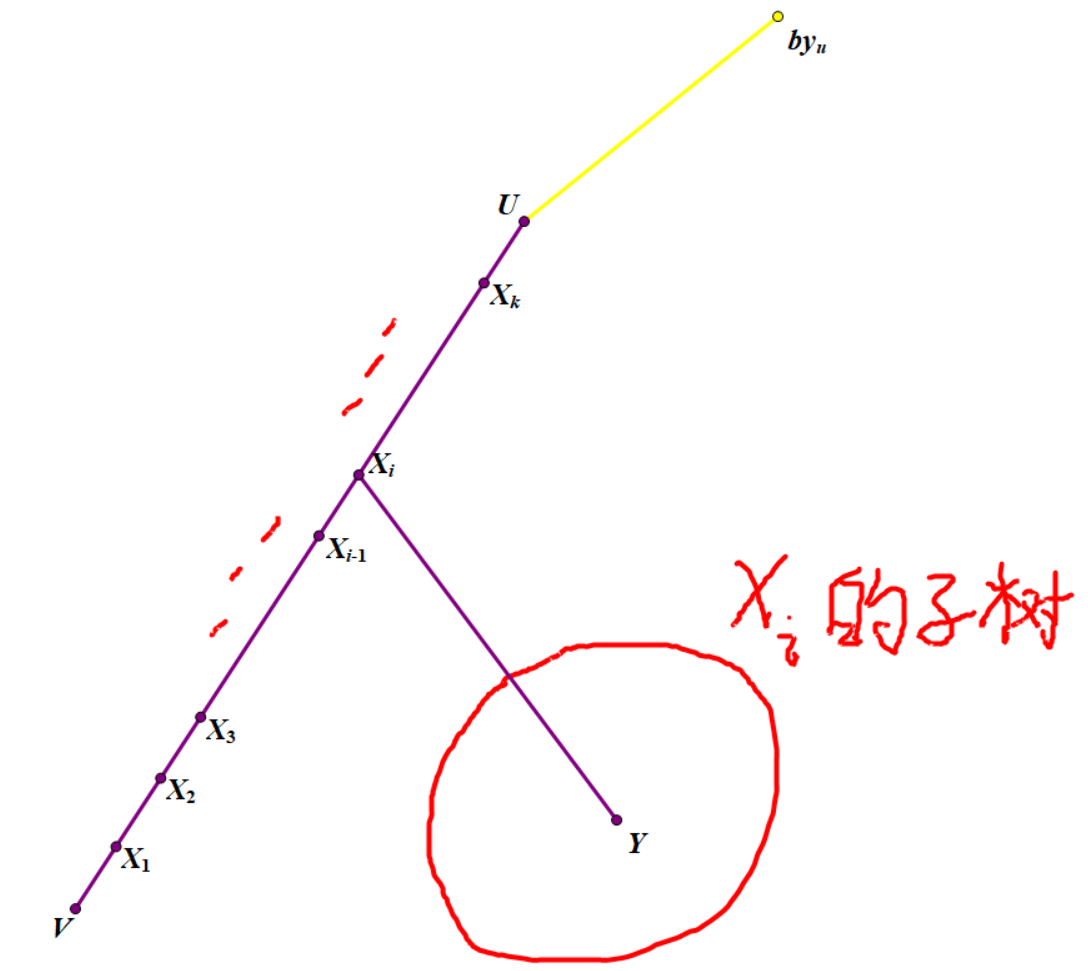
如图所示,\(by_u\) 在 \(u\) 的上方。假设 \(u\to v\) 路径上除 \(u,v\) 外共 \(k\) 个点 \(x_1,x_2,\dots,x_k\)。
考虑 \(x_i\) 子树中某个点 \(y\),\(y\to by_u\) 的路径可以分为三部分:\(y\to x_i,x_i\to u,u\to by_u\),这三部分的长度分别为 \(dep_y-dep_{x_i},dep_{x_i}-dep_u,dist(u,by_u)\),把三者一加,发现是 \(dep_y-dep_u+dist(u,by_u)\),由于 \(u,dist(u,by_u)\) 都是固定的值,故我们只要找到 \(dep_y\) 最大的 \(y\) 就行了。
那么问题又来了,怎么求 \(dep_y\) 最大的 \(y\) 呢?
考虑设 \(sub_i\) 表示 \(i\) 的父亲的子树扣掉 \(i\) 子树后剩余的部分。那么 \((u,v)\) 上的点及其子树内的点恰好就是 \(sub_{v}\cup sub_{x_1}\cup sub_{x_2}\cup\dots\cup sub_{x_{k-1}}\)。记 \(f_i\) 为 \(sub_i\) 中深度的最大值。求出 \(f_v,f_{x_1},f_{x_2},\dots,f_{x_{k-1}}\) 的最大值就行了。这玩意儿可以倍增地求出。
①.2 \(by_u,by_v\) 均在 \(v\) 下方的子树中。
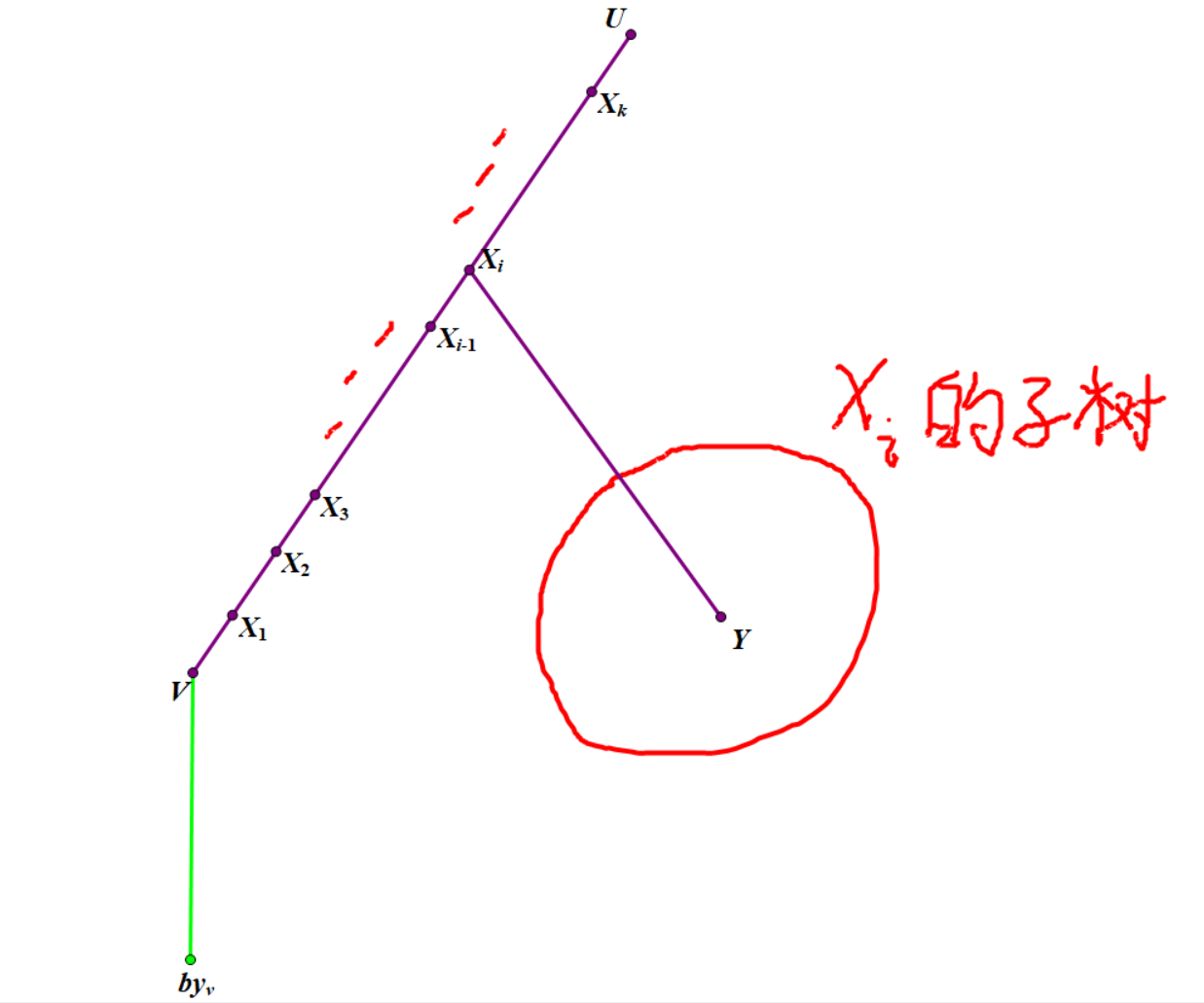
还是考虑 \(x_i\) 子树中某个点 \(y\),\(y\to by_v\) 的路径。这个路径也可以分为三部分:\(y\to x_i,x_i\to v,v\to by_v\),这三部分的长度分别为 \(dep_y-dep_{x_i},dep_v-dep_{x_i},dep_{by_v}-dep_v\),还是将三者加起来,得到 \(dep_y-2\times dep_{x_i}+dep_{by_v}\),设 \(g_i=\) \(sub_i\) 中深度最大值 \(-2\times dep_{fa_i}\)。和前一种情况一样,对 \(g_i\) 倍增一下求个 \(\max\) 就行了。
②. \(by_u\neq by_v\)
和 P3233 一样,求出 \(by_u\) 和 \(by_v\) 管辖的范围,然后对上下两部分分别求一遍 \(f_i,g_i\) 的 \(\max\) 即可。
总结
终于把鸽了两个月,从去年鸽到今年的东西补完了,感动中国
虚树可以解决树上关键点的问题,一般看到 \(\sum k_i\leq 10^5\) 这类字眼就可以想到虚树。因此某道题需要用到虚树很容易,关键在于建好虚树后怎么处理。虚树的题目一般都会跟树形 \(dp\) 相结合。
对于整棵树上的点对答案的贡献,可以将这些点分成两部分:在虚树上的点和不在虚树上的点,不在虚树上的点又可分为两部分:在以虚树上某个点为根的子树中、在虚树上某条边上的节点或其子树内的节点。要对这三部分依次计算贡献。
虚树在实现方面最容易犯的错误就是忘记清空,或者只清空部分变量。因此在求出答案以后记得查看是否所有变量都清空了,另外,切忌直接一遍 memset 清空数组,要对整棵树 dfs 一遍清空。
另外,在将虚树的点按 dfs 序排序的时候,可能会写这样的语句:
sort(pt+1,pt+pn+1,[](int x,int y){return dfn[x]<dfn[y];});
注意这玩意儿要在 C++11 下才能编译通过,如果在模拟赛中



 浙公网安备 33010602011771号
浙公网安备 33010602011771号