欧拉回路小记

都初三了还不会这个就有点丢人了吧

一个相当 water 的东西哦/doge

一些定义

对于图 \(G=(V,E)\)，给出以下定义：

欧拉回路：图 \(G\) 中经过每条边恰好一次的回路。

欧拉路径：图 \(G\) 中经过每条边恰好一次的路径。

欧拉回路的判定

这里不加证明地给出以下定理：

无向图的情况

• 一张无向图 \(G(V,E)\) 有欧拉回路当且仅当它是连通图（注意：这是大前提，很容易被忽略，如果图都不连通了还谈个 P 的欧拉回路呢/cy），并且所有点的度数都是偶数。其中任意一点都可以成为欧拉回路的起点。
• 一张无向图 \(G(V,E)\) 有欧拉路径当且仅当它是连通图，并且度数为奇数的点恰有 \(2\) 个。这两个奇点任意一个都可以作为欧拉路径的起点，另一个也就成为了路径的终点。（P.S.，如果实在记不得，可以想象成我们人为地连一条起点指向终点的边，这样两个奇点都变成了偶点，原本的欧拉路径也就变成了欧拉回路，也进而规约到了欧拉回路的情况）

有向图的情况

类似地，我们也得到的有向图的欧拉路径/回路的判定方式：

• 一张无向图 \(G(V,E)\) 有欧拉回路当且仅当它的基图是连通图，并且所有点所有点的入度等于出度。
• 一张无向图 \(G(V,E)\) 有欧拉路径当且仅当它的基图是连通图，并且恰有一个点满足入度 \(-\) 出度 \(=1\)，也恰有一个点满足出度 \(-\) 入度 \(=1\)，其余点出度都等于入度。

欧拉回路的求法

无向图/有向图的欧拉回路/欧拉路的求法是类似的，知道其中一个的求法也就能顺带着推出另外三个的求法，这里以无向图的欧拉回路的求法为例。

首先任选一个点为起点（由于是欧拉回路，任选一个点为起点都没问题，如果是欧拉路径的情况就按照上面判定的思路找到起点），然后重复以下的操作：从起点开始 DFS，每次访问一个节点 \(u\)，就遍历它的邻居找到一个未访问过的边 \((u,v)\) 并从 \(v\) 点继续 DFS 下去并标记 \((u,v)\) 为“已经访问过”，不难证明我们从 \(v\) 开始 DFS 下去的过程中一定会回溯到 \(u\)，也就是从 DFS \(v\) 到回溯到 \(u\) 的部分一定还是一个欧拉回路（否则假设 \(v\) 到达某个点 \(w\) 之后无路可走了，那么在这之前由于每次访问 \(w\) 都是从某个点到达 \(w\)，再从 \(w\) 走向某个点，会消灭掉 \(2\) 条与 \(w\) 相连的边，而这次访问到 \(w\) 时只消灭了一条与 \(w\) 相连的边，之后 \(w\) 的度数就变为 \(0\) 了，也就是说 \(w\) 的度数为奇数，与欧拉回路的条件“所有点的度数都是偶数”矛盾）。回溯的时候就将边 \((u,v)\) 的信息压入 DFS 序列。正确性显然。

不过这个做法的复杂度是错误的，比方说下图：

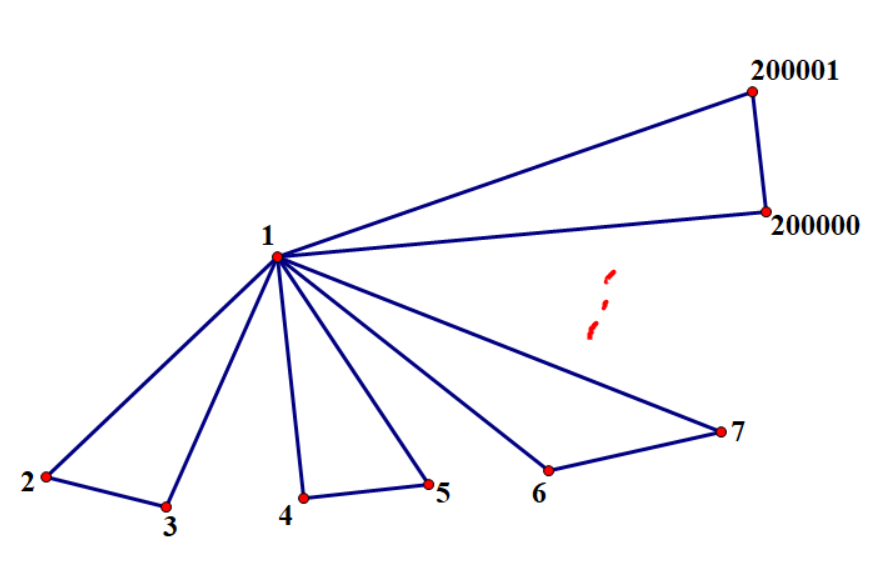
不难发现我们回溯到 \(1\) 的次数为 \(10^5\)，而我们每次回溯到 \(1\) 都要从头开始寻找第一个未访问过的边，也就是说当我们访问最后几个环的时候这个访问次数最高可达 \(10^5\)，时间复杂度也就退化到了 \(10^5\times 10^5=10^{10}\)，直接爆炸。这里可以借鉴网络流中“当前弧优化”的思想，记录一个 \(now_x\) 表示当前访问到了哪条边，每次寻找第一个未访问过的边时就从 \(now_x\) 开始遍历即可，这样复杂度就降到了 \(\mathcal O(|E|)\)。相信学过网络流的同学这一步都不难理解。

int hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=1;//边从 1 开始编号
bool used[MAXN+5];vector<int> ret;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
void cir(int x){
	for(int &e=hd[x];e;e=nxt[e]) if(!used[e>>1]){
		used[e>>1]=1;int tmp=e;//注意保存临时变量
		cir(to[e]);ret.pb(e);
	}
}