长链剖分小记
开坑待填
UPD on 2021.3.25:终于学到这个了,之前二月份的时候就说要学来着的?下次争取不做鸽子/xk/xk
长链剖分,顾名思义,就是将树链剖分中重儿子的定义由“大小最大的节点”改为“子树内深度最深的节点深度最大的节点”,或者给它一个新定义叫做“深儿子”。和树链剖分一样,我们还是将每个节点与其深儿子之间的边称为“深边”,深边组成的链称为“长链”。
长链剖分与树链剖分有众多相似之处,因此它们被统称为树链剖分,下面列出了一些长链剖分的性质:
- 每个点恰好属于一条长链,即重链的长度之和为 \(\mathcal O(n)\) 级别,证明显然(对于重链剖分,此条性质依旧成立)
- 每棵树的长链个数等于其叶子节点个数,证明显然(对于重链剖分,此条性质依旧成立)
- 对于每个点,其到根节点路径上经过的长链个数是 \(\mathcal O(\sqrt{n})\) 级别的,这个与重链剖分不同,因为我们每遇到一条新的重链,都有新的长链长度 \(\ge\) 原来的长链长度 \(+1\),最坏情况下我们遇到的长链长度为 \(1,2,3,\cdots\),最多写 \(\mathcal O(\sqrt{n})\) 级别个数,它们的和就达到了 \(n\)(不过似乎不知道这条性质有什么用?)。
代码与重链剖分大同小异:
void dfs(int x=1,int f=0){
fa[x][0]=f;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];if(y==f) continue;
dep[y]=mxdep[y]=dep[x]+1;dfs(y,x);
if(mxdep[y]>mxdep[x]) mxdep[x]=mxdep[y],wson[x]=y;
}
}
长链剖分的几个应用
\(\mathcal O(n\log n)-\mathcal O(1)\) 求树上 \(k\) 级祖先
首先这里有一个引理,就是树上任意一个节点 \(x\) 的 \(k\) 级祖先所在长链的长度 \(\ge k\),证明异常简单,非常显然的一点是对于任意一点 \(x\),\(x\) 所在长链中 \(x\) 到链底部分的长度为 \(mxdep_x-dep_x\),其中 \(mxdep_x\) 为 \(x\) 子树内节点深度的最大值。假设 \(x\) 的 \(k\) 级祖先为 \(y\),那么显然 \(mxdep_y\ge dep_y+k\),因为 \(y\) 子树内已经有一个深度为 \(dep_y+k\) 的点 \(x\) 了,故 \(y\) 所在长链长度 \(\ge mxdep_y-dep_y\ge k\),得证。
考虑有了这个性质之后怎样 \(\mathcal O(1)\) 出 \(x\) 的 \(k\) 级祖先。考虑 \(k\) 二进制下最高位 \(2^r\),显然 \(k-2^r<2^r\),我们预处理出每个点的 \(2^i\) 级祖先,并先将 \(x\) 跳到其 \(2^r\) 级祖先的位置 \(x'\),我们再将 \(x'\) 跳到 \(x'\) 所在重链链顶 \(x''\) 处,还剩 \(k'=k-2^r-(dep_{x'}-dep_{x''})\) 步,显然若 \(k'>0\) 那么原来 \(x\) 的 \(k\) 级祖先就是 \(x''\) 的 \(k'\) 级祖先,否则 \(x\) 的 \(k\) 级祖先为 \(x''\) 沿 \(x''\) 所在重链向下走 \(-k'\) 步走到的节点。我们对于每个链的链顶节点 \(x\) 开两个 std::vector<int>,分别叫 \(up\) 和 \(down\),假设 \(x\) 所在长链长度为 \(l\),那么我们就预处理 \(x\) 的 \(0,1,\dots,l\) 级祖先以及 \(x\) 沿重链向下走 \(0,1,\dots,l\) 步得到的节点,显然这样预处理是时间复杂度与所有重链长度之和同阶,为 \(\mathcal O(n)\)。回到刚刚的过程来,若 \(k'>0\),则根据预处理的值返回 \(up_{x,k'}\) 即可,反之返回 \(down_{x,-k'}\)。根据「引理」可知 \(x''\) 所在长链长度 \(\ge 2^r+dep_{x'}-dep_{x''}\ge k'=k-2^r-(dep_{x'}-dep_{x''})\),同时 \(2^r+dep_{x'}-dep_{x''}\ge 2^r+dep_{x'}-dep_{x''}-k=-k'\),因此 \(x''\) 所在长链长度 \(\ge|k'|\),因此该做法是没问题的。
int top[MAXN+5];
vector<int> up[MAXN+5],dw[MAXN+5];
void dfs2(int x=1,int tp=1){
top[x]=tp;
if(x==tp){
for(int i=0,cur=x;i<=mxdep[x]-dep[x];cur=fa[cur][0],i++) up[x].pb(cur);
for(int i=0,cur=x;i<=mxdep[x]-dep[x];cur=wson[cur],i++) dw[x].pb(cur);
} if(wson[x]) dfs2(wson[x],tp);
for(int e=hd[x];e;e=nxt[e]) if(to[e]!=wson[x]) dfs2(to[e],to[e]);
}
int getkth(int x,int k){
if(!k) return x;int lg=31-__builtin_clz(k);
x=fa[x][lg];k-=1<<lg;k-=dep[x]-dep[top[x]];x=top[x];
return (k>=0)?up[x][k]:dw[x][-k];
}
类似 dsu on tree 的东西
我们知道若一个子树维护的信息量为 \(\mathcal O(sz_x)\),那可以用树上启发式合并实现 \(\mathcal O(n\log n)\) 维护子树信息。那么如果一个子树维护的信息量为 \(\mathcal O(mxdep_x-dep_x)\) 呢?此时长链剖分就要派上用场了。将 dsu on tree 中的大小最大儿子改为最大深度最深的儿子即可实现线性维护子树信息。
证明:对于每个点 \(x\),显然只有它的浅儿子 \(y\) 的子树信息会被重新统计,因此复杂度为 \(x\) 所有浅儿子的 \(mxdep_y-dep_y\) 之和,而由于浅儿子与长链形成双射,因此可以看作对于每条长链,其只会在链顶的父亲处产生 \(\mathcal O(|\text{长链长度}|)\) 的贡献,由长链长度之和为 \(\mathcal O(n)\) 级别的可知复杂度是线性的。
在使用长链剖分维护与深度有关的信息时,一般都要使用指针分配内存,来模拟数组的偏移。
例题
u1s1 感觉长链剖分的应用就这么多,剩下的就是具体情况具体分析了(
1. CF1009F Dominant Indices
大概可以算得上长链剖分后一个应用的 mbt(?)
我们记 \(f_{u,i}\) 为距离 \(u\) 为 \(i\) 的节点个数,那么答案即为使二元组 \(f_{u,i}\) 取到最大值的 \(i\)。
那么显然有转移方程 \(f_{u,i}=\sum\limits_{v\in son_u}f_{v,i-1}\),\(f_{u,0}=1\)。
暴力转移显然是不行的。不过看到这种与深度有关的题目,可以考虑长链剖分,按照 dsu on tree 的套路,我们 DFS 到 \(u\) 的时候,先遍历所有 \(u\) 的浅儿子并统计其子树的答案,清空桶。如果 \(u\) 存在深儿子,那就再遍历 \(u\) 的深儿子 \(v\) 并直接从 \(f_v\) 转移到 \(f_u\)(根据上面的状态转移方程,这一步相当于数组向右一位),再遍历一遍 \(u\) 的浅儿子并直接将 \(u\) 的浅儿子的桶与 \(u\) 的桶合并,时间复杂度线性。
口胡起来异常容易,不过实现起来还是有些困难的。因为如果暴力开数组的话时空都会爆炸,无法通过。注意到当我们从 \(u\) 的重儿子的桶继承到 \(u\) 时,我们希望这一步能做到 \(\mathcal O(1)\),而这一步的本质相当于将数组向右移一位,因此可以想到指针。具体来说我们事先开辟一个长度为 \(n\) 的 int 数组 tmp 和一个动态指针 pt,初始 \(pt\) 为 \(tmp\) 的起始位置,\(f\) 数组开成指针的形式(指针数组),每次递归深儿子的时候,就事先将 \(f_v\) 设为 \(f_u\) 向右偏移一位的位置,这样能够保证 \(f_u\) 为 \(f_v\) 向右移一位了,当我们递归浅儿子 \(v'\) 的时候,我们就令 \(f_{v'}=pt\),并令 \(pt\leftarrow pt+mxdep_{v'}-dep_{v'}\),相当于为 \(f_{v'}\) 开辟了长度为 \(mxdep_{v'}-dep_{v'}\) 的一段内存,显然这样复杂度线性,符合要求。
当然这题也有不用指针的方法,考虑对每个 \(u\) 开辟一个 vector 记录 \(f_{u,i}\) 的值,当我们遍历重儿子时就交换其与 \(u\) 的 vector 值,那么怎样实现数组右移呢?由于 vector 在开头插值不方便,我们考虑将整个 vector 整体 reverse 过来,这样在开头插值就变成了在结尾插值,就很方便了。遍历浅儿子时直接合并即可,复杂度还是线性的。
u1s1 这题虽然水但是值得挖掘的东西还挺多的呢
2. P3899 [湖南集训]谈笑风生
这题在我很多很多年以前学主席树的时候曾被当作主席树模板题看待,现在学到长链剖分则把它当作长链剖分的模板题看待。
考虑什么样的点对 \((a,b,c)\) 满足条件,由于 \(a,b\) 都为 \(c\) 的祖先,那 \(a,b\) 必然也是祖先关系,据此可分两种情况:
- \(b\) 为 \(a\) 的祖先,那显然可能的 \(b\) 有 \(\min(dep_a,k)\) 个,可能的 \(c\) 组成的集合为 \(a\) 子树内的节点扣掉 \(a\),共 \(\min(dep_a,k)\times (sz_a-1)\) 种可能
- \(a\) 为 \(b\) 的祖先,那么 \(b\) 必定在 \(a\) 的子树中,并且深度 \(\le dep_a+k\),\(c\) 必定在 \(b\) 的子树中,并且不同于 \(b\),因此对于一种可能的 \(b\),可能的 \(c\) 的个数为 \(sz_b-1\),也就是说我们要统计 \(a\) 子树内所有深度 \(\le dep_a+k\) 的点 \(b\) 的 \(sz_b-1\) 之和,这个可以通过长链剖分+后缀和实现线性求解,具体来说我们开一个桶 \(cnt_i\) 维护当前子树内深度 \(\ge i\) 的点的 \(sz-1\) 之和。当我们 DFS 到某个点 \(u\) 的时候,我们开一个
vector<vector<int> >维护 \(u\) 所有轻儿子的桶的集合,我们遍历所有轻儿子 \(v\),然后将 DFS \(v\) 时候的 \(cnt_{dep_v}\) 到 \(cnt_{mxdep_v}\) 存入一个vector,并将这个vector压入我们vector<vector<int> >中,然后 DFS \(u\) 的重儿子,由于这里 \(cnt\) 的定义与深度,而不是距离 \(u\) 的距离有关,因此不需要什么右移数组,然后遍历之前保存的vector<vector<int> >将对应位置的值累加上去即可,最后算上 \(u\) 本身的贡献,复杂度线性。
const int MAXN=3e5;
int n,qu,hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int dep[MAXN+5],mxdep[MAXN+5],wson[MAXN+5],siz[MAXN+5];
void dfs1(int x=1,int f=0){
siz[x]=1;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];if(y==f) continue;
dep[y]=mxdep[y]=dep[x]+1;dfs1(y,x);siz[x]+=siz[y];
if(mxdep[y]>mxdep[x]) mxdep[x]=mxdep[y],wson[x]=y;
}
}
ll cnt[MAXN+5];vector<pii> qv[MAXN+5];
ll ans[MAXN+5];
void dfs2(int x=1,int f=0){
vector<vector<ll> > t;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];if(y==f||y==wson[x]) continue;dfs2(y,x);vector<ll> tmp;
for(int j=dep[y];j<=mxdep[y];j++) tmp.pb(cnt[j]),cnt[j]=0;
t.pb(tmp);
} if(wson[x]) dfs2(wson[x],x);
for(int i=0;i<t.size();i++) for(int j=0;j<t[i].size();j++)
cnt[dep[x]+1+j]+=t[i][j];
cnt[dep[x]]=cnt[dep[x]+1]+siz[x]-1;
for(int i=0;i<qv[x].size();i++){
ans[qv[x][i].se]=cnt[dep[x]+1]-cnt[min(dep[x]+qv[x][i].fi,mxdep[x])+1]
+1ll*min(dep[x],qv[x][i].fi)*(siz[x]-1);
}
}
int main(){
scanf("%d%d",&n,&qu);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
adde(u,v);adde(v,u);
} dfs1();
for(int i=1,x,y;i<=qu;i++) scanf("%d%d",&x,&y),qv[x].pb(mp(y,i));
dfs2();for(int i=1;i<=qu;i++) printf("%lld\n",ans[i]);
return 0;
}
3. CF208E Blood Cousins
…………更板的题?
首先对于每组询问求出 \(x\) 的 \(k\) 级祖先 \(y\),若 \(y=0\) 则答案为 \(0\),否则答案为 \(y\) 子树内深度为 \(dep_y+k\) 的点的个数 \(-1\),考虑把每组询问挂在 \(y\) 上,长链剖分一下求一遍答案即可,复杂度线性。
4. P5384 [Cnoi2019]雪松果树
题意同上一题,不过数据范围加强到了 \(10^6\),空间限制也卡到了 \(128\text{MB}\),因此不能用什么倍增求 \(k\) 级祖先,否则会 \(\text{MLE}\),长链剖分求 \(k\) 级祖先也会 \(\text{MLE}\),这里考虑离线求 \(k\) 级祖先,具体来说,对每组 \((x,k)\) 我们将其挂在 \(x\) 上,然后对树进行一遍 DFS,用栈记录当前点的祖先序列,即可实现 \(\mathcal O(1)\) 求 \(k\) 级祖先。然后按照上一题的套路长链剖分一下即可,复杂度线性。
还有一点需提醒的是,这题空间卡得较紧,稍不注意就会 \(\text{MLE}\),比方说 std::vector 空间常数较大(大约程序会自动开 3 倍空间),如果在程序中使用较多 vector<int> 就有 \(\text{MLE}\) 的风险,建议使用链式前向星。
5. P5904 [POI2014]HOT-Hotels 加强版
不妨以 \(1\) 为根,考虑合法的三元组 \((x,y,z)\) 可能长什么样:
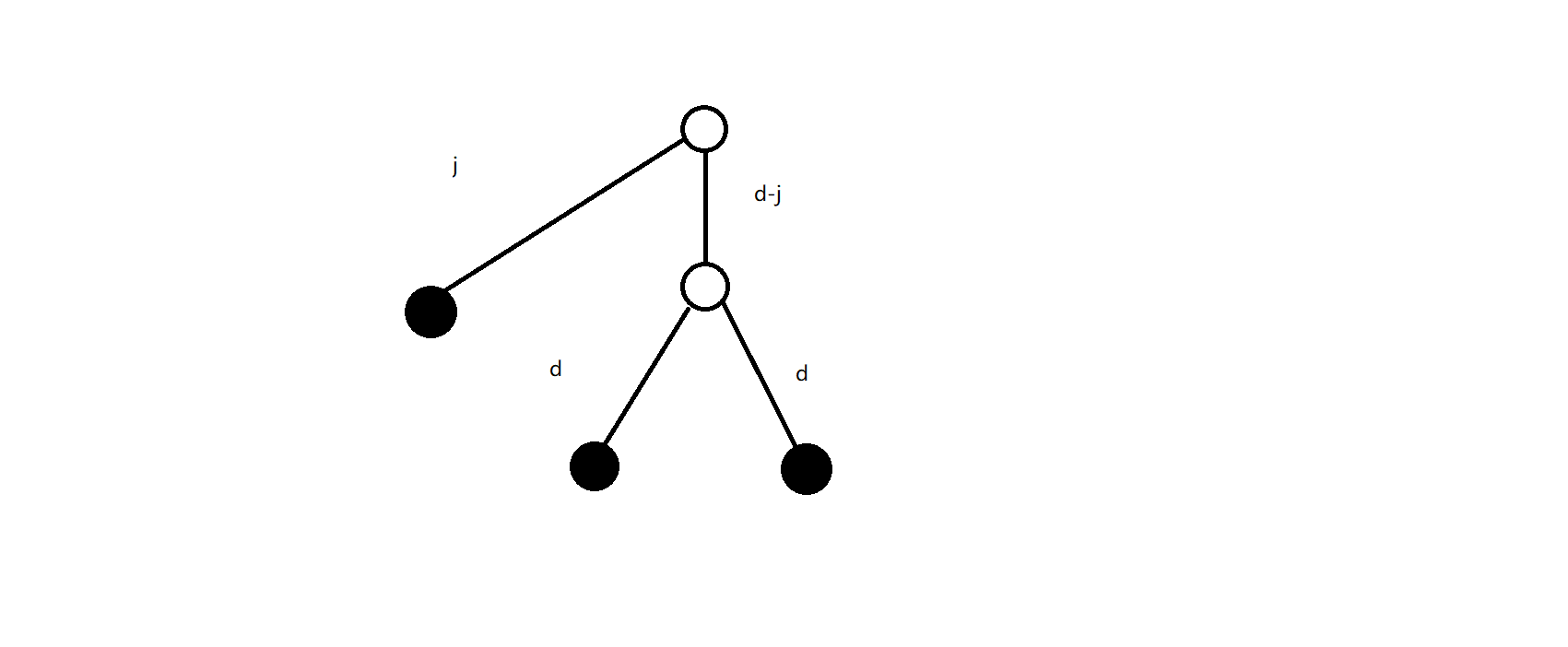
当然也有两个特例,左边的图是 \(j=d\) 的特例,右边的图是 \(j=0\) 的特例:
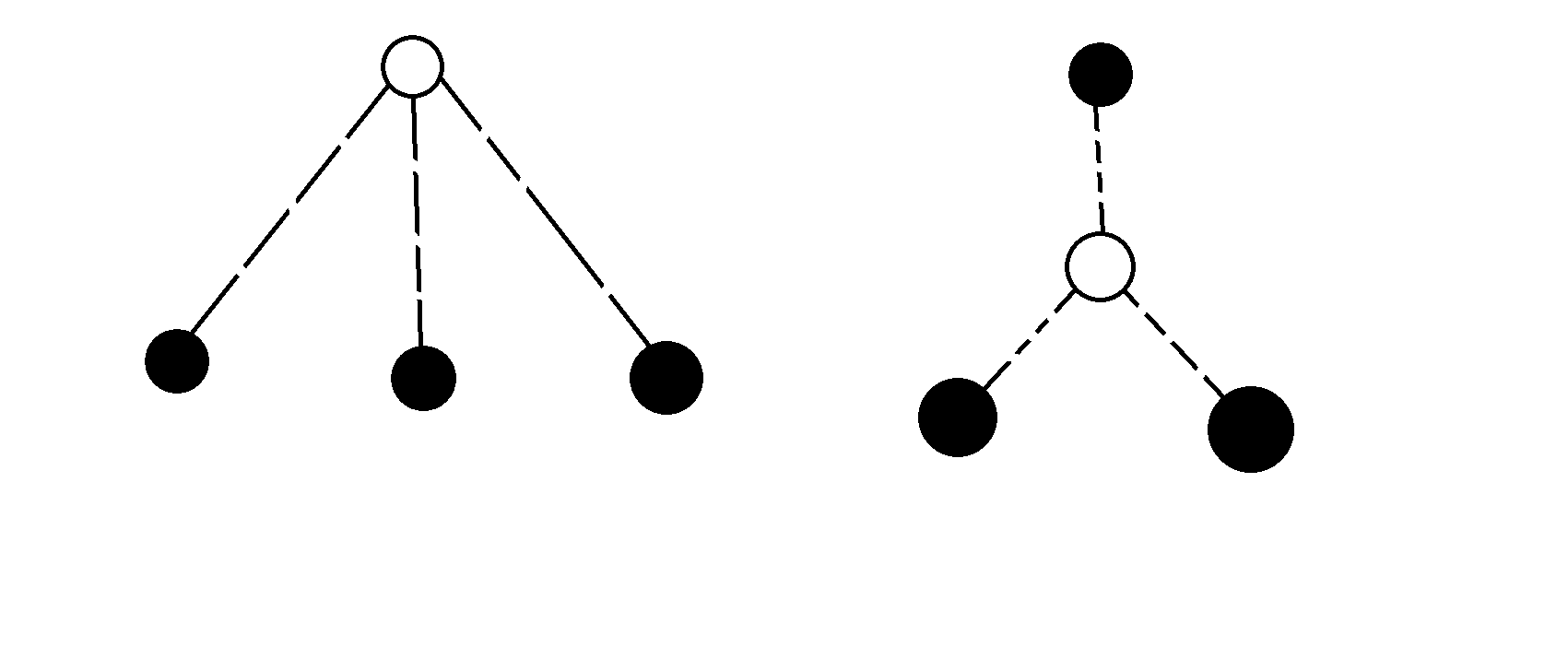
考虑 \(dp\),\(f_{i,j}\) 表示在 \(i\) 的子树中到 \(i\) 的距离为 \(j\) 的节点个数,\(g_{i,j}\) 表示满足 \(u,v\) 都在 \(i\) 的子树中,并且 \(\text{dis}(u,\text{LCA}(u,v))=\text{dis}(v,\text{LCA}(u,v))=\text{dis}(\text{LCA}(u,v),i)+j\) 的点对 \((u,v)\) 的个数。
那么有转移:
- \(ans\leftarrow g_{u,0}\)
- \(ans\leftarrow f_{x,j-1}\times g_{y,j+1}(x,y\in son(u),x\ne y)\)
- \(g_{i,j}\leftarrow g_{x,j+1}(x\in son(u))\)
- \(g_{i,j}\leftarrow f_{x,j-1}\times f_{y,j-1}(x,y\in son(u),x\ne y)\)
- \(f_{i,j}\leftarrow f_{i,j-1}\)
长链剖分优化一下即可,时间复杂度 \(\mathcal O(n)\)。
6. CF504E Misha and LCP on Tree
这是道 *3000 的 D1E,不过感觉这个 *3000 显然难度不到 *3000 吧,连我这种蒟蒻都能不看题解 AC……
毫无思维难度,直接二分 LCP 长度,哈希 check 一下即可,哈希 check 的过程中要用到求一个点的 \(k\) 级祖先,而由于此题 \(m\) 数据范围高达 \(10^6\),故使用倍增跳 father 的做法会 TLE,需使用长链剖分,复杂度 \(m\log n\),中间还有几个细节需注意。
卡时限过题真 nm 有趣
7. BZOJ 3252 攻略
事实上是一个非常愚蠢的贪心。
按照点权和的大小划分长链(广义长链),然后将所有的链排个序,选前 \(k\) 个即可,时间复杂度 \(\mathcal O(n\log n)\)。
8. CF526G Spiders Evil Plan
用到的思想还是长链剖分优化贪心,不过比上一题不知道强到哪里去了……



 浙公网安备 33010602011771号
浙公网安备 33010602011771号