Floyd算法,以动态规划为理论基础,poj1125
Floyd是用于查找图中每一对顶点之间的最短距离,是以动态规划为基础的算法;
基本思想:若现在要求vi到vj的最短路径,设vi到vj的路径dis(vi,vj)即为最短路径,可将dis(vi,vj)与dis(vi,v0,vj)进行比较(其中v0表示vi到vj之间的一个结点,即vi能通过v0到达vj),取较小值,然后在此较小值上再增加一个结点v1,将dis(vi,...,v1,...,vj)和已经得到的从vi到vj的较小值比较,取较小值;再增加一个结点v2,以此类推,最终便可得到vi到vj的最短路径。
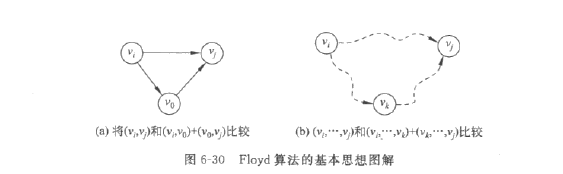
由上述可得出递推公式(arc表示i到j的直接路径,若没有,用一个极大值0x3f3f3f3f代替):

上代码:
void floyd(int n){ for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if(a[i][k]+a[k][j]<a[i][j]){ a[i][j] = a[i][k]+a[k][j]; } } } } }
接下来上一个例题,poj1125.
题目描述:炒股为了获得高收益,投资人需要释放谣言引起恐慌,投资人目前有几个手下专门用于释放谣言,最后要使得他们都知道这个谣言,要求输入这几个手下之间互相传递信息的时间,信息可同时传递,输出使他们都知道消息的最短时间方案(以谁为消息源,时间是多少).
输入:
包含多个输入样例,以0结束,开头输入一个n表示n个手下,接下来输入n行,每行开头输入一个m表示这个手下与多少个人有联系,紧接着输入m组数据表示这个手下与哪个手下有联系以及传播时间
输出:
消息源手下编号,最短时间
样例输入:
3 2 2 4 3 5 2 1 2 3 6 2 1 2 2 2 5 3 4 4 2 8 5 3 1 5 8 4 1 6 4 10 2 7 5 2 0 2 2 5 1 5 0
样例输出:
3 2 3 10
分析:很明显此题要求的是,从一个结点出发到其他所有结点的最短路径,且可在同一时间进行传播,那么首先要用floyd求出每个结点之间的最短路径,
由于可在同一时间进行传播这一条件,最终的完成时间肯定是这个结点到其他节点最短路径的最大值,那么只需找出这些对大致当中的最小值便是最短时间,并记录对应下标便是消息源
代码如下:
#include<iostream> #include<cstring> using namespace std; const int MAX = 0x3f3f3f3f; int a[105][105]; /* poj 1125 floyd算法 */ void floyd(int n){ for(int k=1;k<=n;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if(a[i][k]+a[k][j]<a[i][j]){ a[i][j] = a[i][k]+a[k][j]; } } } } } int main(){ int n; int res; while(cin>>n,n!=0){ int min=0x3f3f3f3f; memset(a,MAX,sizeof(a)); for(int i=1;i<=n;i++){ int m; cin>>m; for(int j=0;j<m;j++){ int temp; cin>>temp; cin>>a[i][temp]; } } floyd(n); for(int i=1;i<=n;i++){ int max=0; for(int j=1;j<=n;j++){ if(i==j) continue; if(a[i][j]>max){ max=a[i][j]; } } if(max<min){ min=max; res=i; } } cout<<res<<" "<<min<<endl; // for(int i=1;i<=n;i++){ // for(int j=1;j<=n;j++){ // cout<<a[i][j]<<" "; // } // cout<<endl; // } } return 0; }



