为什么HashMap扩容是2倍以及容量为什么是2的n次幂

** java8**
为什么HashMap扩容是2倍以及容量为什么是2的n次幂，和这个数组下标的计算方法有着千丝万缕的关系。
先看看计算数组下标源码：

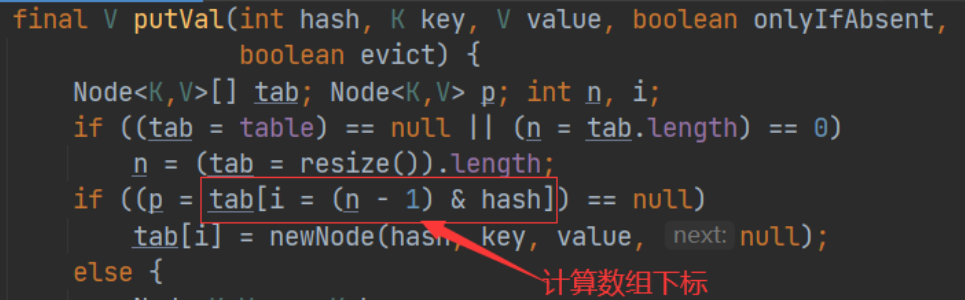
由上图我们可以看到，<key,value>要放到数组的那个位置，它会通过key的hash值和数组长度-1进行与运算来计算得出。也就是
(n - 1) & hash

这里n就是数组长度。可以看出一旦数组扩容，算式中n就发生了变化，那么原来元素下标也会发生变化，<key,value>就要移动位置。
如果每一次扩容所有的<key,value>都要移动，势必带来性能上的不足。
但是当扩容是2倍，我们就会发现非常有趣的地方。
我们来看一下hashmap的扩容过程。
16（默认）-> 32(扩容一次) -> 64(扩容两次)
从10进制中我们或许发现不了什么，但是它是进行与运算所以咱们只要二进制，这时就有点意思了。

0001 0000    //16二进制    
0010 0000    //32二进制  
0100 0000    //64二进制

-1之后则变为

0000 1111     
0001 1111  
0011 1111

比如现在我们有三个<key,value>要插入，通过计算key的hash值分别为

0101 1010 0011 1101
0101 1010 0011 1101
1110 0100 0001 0001

代入计算之后

hashCode(计算的hash值只用高16)	size=16	size=32	是否移位
1010 0011 1101	1010 0011 1101&1111	1010 0011 1101&11111	向前移动16位
1010 0011 1101	1010 0011 1101&1111	1010 0011 1101&11111	不用移位
0100 0001 0001	0100 0001 0001&1111	0100 0001 0001&11111	向前移动16位

我们发现，扩容后是否移位，由扩容后key的hashcode参与计算的最高位是否1为所决定，并且移动的方向只有一个，即向高位移动。因此，可以根据对最高位进行检测的结果来决定是否移位，从而可以优化性能，不用每一个元素都进行移位，

是否移位，由扩容后表示的最高位是否1为所决定，并且移动的方向只有一个，即向高位移动。因此，可以根据对最高位进行检测的结果来决定是否移位，从而可以优化性能，不用每一个元素都进行移位。最高位为0 与运算之后的值依然与之前相同说明不用向高位移动。为1则需要向高位移动。

结论，原因有二：#

第一哈希函数的问题将元素充分散列，避免不必要的哈希冲突。
通过除留余数法方式获取桶号，因为Hash表的大小始终为2的n次幂，因此可以将取模转为位运算操作，提高效率，容量n为2的幂次方，n-1的二进制会全为1，位运算时可以充分散列，避免不必要的哈希冲突。
第二就是扩容时桶内元素是否向高位移动的问题。扩容为2倍，参与计算的hashcode高位为1则移动，为0则不移动，也就是说一个桶内元素只有一半的概率需要移动，从而优化了性能。