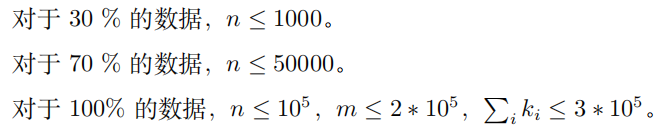JZOJ-2019-11-5 A组
T1
给定由 n 个点 m 条边组成的无向连通图,保证没有重边和自环。
你需要找出所有边,满足这些边恰好存在于一个简单环中。一个环被称为简单环,当且仅当它包含的所有点都只在这个环中被经过了一次。(即求\(\oplus \{id((u,v)) | (u,v) \in E 且 (u,v)在且仅在一个环上\}\))
注意到这些边可能有很多条,你只需要输出他们编号的异或和即可。
Input
第一行两个数 n, m。
接下来 m 行,每行两个数 ai , bi,表示第 i 条边连接了 ai , bi。
Output
输出一个数,表示所有满足条件的边的编号的异或和。
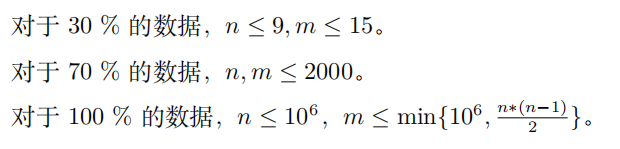
前置知识
解法1
树上差分, LCA, 巨大码力
解法2
Tarjan 算法求强连通分量
解法1
可以先 dfs 出一棵生成树。
因为是无向图,生成树上的非树边都是返祖边,我们容易发现,若一条边恰好在一个简单环内,那么它满足下面下面两个条件之一:
- 返祖边,且它覆盖的树边不和任何其他返祖边覆盖的树边有公共边。
- 树边且被一条返祖边覆盖,覆盖它的返祖边覆盖的树边不和其他返祖边覆盖的树边有公共
边。
可以先对于每条树边 O(n) 求出被多少条返祖边覆盖,然后对于每条返祖边 O(m) 计算是否跟其他返祖边有重合。时间复杂度 O(nm)。计算被多少返祖边覆盖可以利用树上差分的思想做到 O(m),计算是否有重合相当于链上查询,也可以利用差分做到 O(m)。时间复杂度 O(n + m)。代码贼难写考场上数组开多MLE了血亏100pts
解法2
考虑求出所有的点双连通分量。首先这个点双连通分量里的边要合法的话,那么内部的边数一定大等于点数(因为有环)。其次这个点双连通分量里如果边数大于点数,那么所有边可以由两个不同的环覆盖。
也就是说,我们只需要求出所有的点双连通分量,然后把那些点数等于边数的点双连通分量内部的边标记为合法即可。利用 \(Tarjan\) 算法求强连通分量可以做到 \(O(n + m)\)。
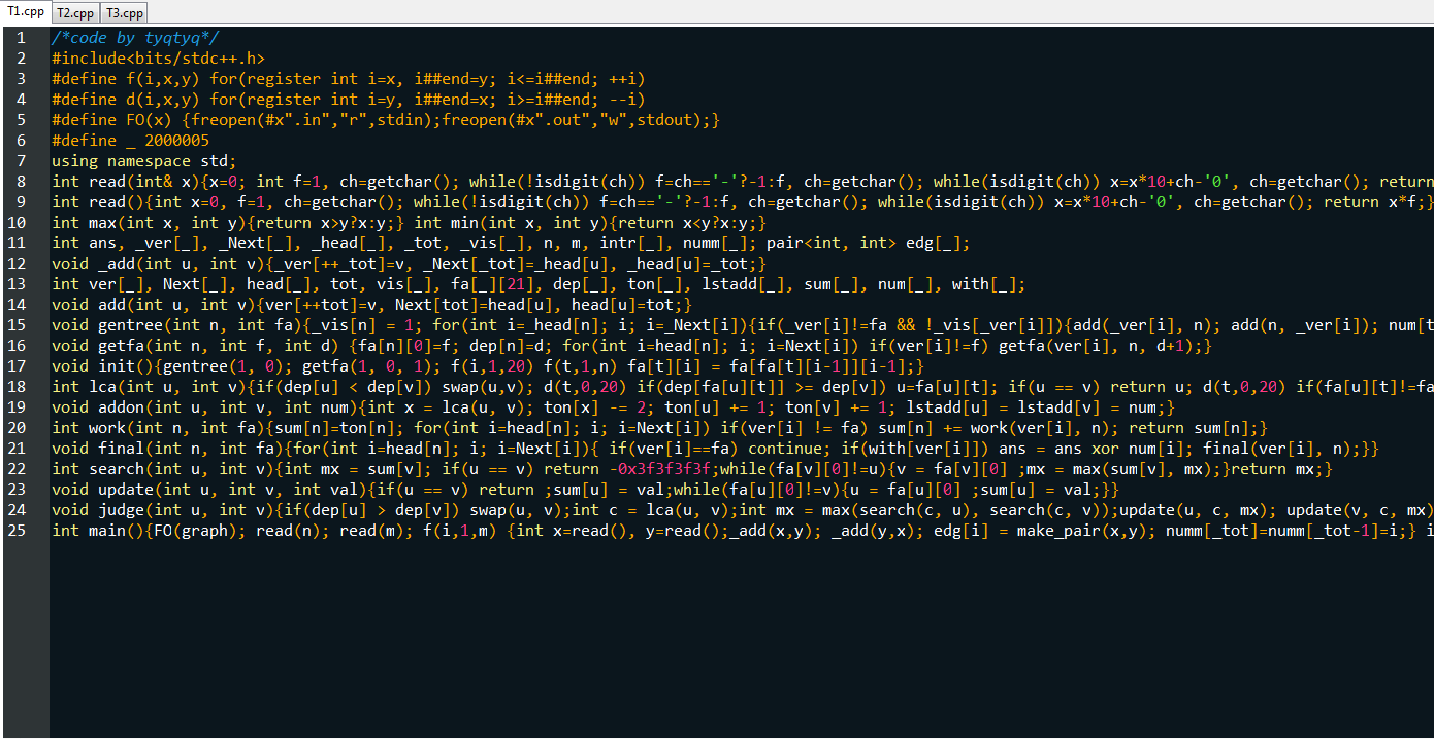
代码
/*code by tyqtyq*/
#include<vector>
#include<cstdio>
#include<iostream>
#define f(i,x,y) for(register int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(register int i=y, i##end=x; i>=i##end; --i)
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define _ 2000005
using namespace std;
int read(int& x){x=0; int f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*=f;}
int read(){int x=0, f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*f;}
int max(int x, int y){return x>y?x:y;} int min(int x, int y){return x<y?x:y;}
int Next[_], ver[_], head[_], tot=1, dfn[_], low[_], cnt, stack[_], top, vis[_], V[_], ans;
vector<int> dcc, orz;
void add(int u, int v){ver[++tot]=v, Next[tot]=head[u], head[u]=tot;}
void dfs(int x){
for(int i=head[x];i;i=Next[i]){
if(!V[ver[i]]||vis[i]) continue;
vis[i]=vis[i^1]=1;
orz.push_back(i);
dfs(ver[i]);
}
}
void tarjan(int x, int root){
dfn[x] = low[x] = ++cnt;
stack[++top] = x;
int flag=0;
for(int i=head[x];i;i=Next[i]){
int v=ver[i];
if(!dfn[v]){
tarjan(v, root); low[x]=min(low[x], low[v]);
if(low[v] >= dfn[x]){
++flag; int d; do{d=stack[top--]; dcc.push_back(d); V[d]=1;}while(d!=v); dcc.push_back(x); dfs(x) ;
if(orz.size() == dcc.size()) for(auto j:orz) ans^=(j/2),vis[j]=vis[j^1]=0;
for(auto j:dcc) V[j]=0; dcc.clear(); orz.clear();
}
}
else low[x]=min(low[x], dfn[v]);
}
}
int n, m;
int main(){
read(n); read(m);
f(i,1,m) {int x,y; read(x); read(y); add(x,y); add(y,x);}
tarjan(1, 1);
cout<<ans<<endl;
return 0; //拜拜程序~
}
T2
\(Wayne\)喜欢看书,更喜欢买书。
某天\(Wayne\)在当当网上买书,买了很多很多书。\(Wayne\)有一个奇怪的癖好,就是第一本书的价格必须恰为\(X\),而之后买的每一本书,若是比上一本更昂贵,则价格最多多\(A\)元;若是比上一本更便宜,则价格最多少\(B\)元。
\(Wayne\)心血来潮,一口气买了\(N\)本书,但他记不得每本书的价格了,只记得总价格是\(M\)。\(Wayne\)于是很想知道一种可能的书价分布。为了简化问题,我们假定书价的定义域是整数,且每本书与上一本书的价格差,要么恰为\(+A\),要么恰为\(-B\)。
只要给出任意一个合法的书价序列就算正确。
Input
第一行一个正整数N。
第二行四个整数依次是X,A,B,M。
Output
输出一行N个整数,用空格隔开。数据保证有解。
Data Constraint
对于\(100%\)的数据,满足\(1 \leq A, B \leq 10^6,|X| \leq 10^6,N \leq 10^5\),\(M\)可用带符号\(64\)位整型存储。
前置知识
推式子能力
解法
设买书编号为\(0-n\), \(a_i\)表示当前升了几次价格
对于\(a_i\), 总有\(a_i = a_{i-1} + 1\) 或 \(a_i = a_{i-1}\)成立, 且必有\(a_0 = 0\)
有总买书价格为\(\sum_{i=0}^{n} x + a_i \times A - (k-a_i) \times B\) = \(n \times x - B \times \frac{n \times (n+1)}{2} \sum_{i=0}^{n} a_i \times(A+B)\), 整理得\(\sum_{i=0} a_i = \frac{m - n \times x + B \times \frac{n \times (n+1)}{2}}{A+B}\)
因总有\(a_i = a_{i-1} + 1\) 或 \(a_i = a_{i-1}\)成立, 考虑求出差分序列\(\delta(a)\), 总有\(\delta(a)_i = 0\) 或 \(\delta(a)_i = 1\)成立, 做一遍整数拆分即可
代码
/*code by tyqtyq*/
#include<bits/stdc++.h>
#define f(i,x,y) for(register int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(register int i=y, i##end=x; i>=i##end; --i)
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define int long long
using namespace std;
int read(int& x){x=0; int f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*=f;}
int read(){int x=0, f=1, ch=getchar(); while(!isdigit(ch)) f=ch=='-'?-1:f, ch=getchar(); while(isdigit(ch)) x=x*10+ch-'0', ch=getchar(); return x*f;}
int max(int x, int y){return x>y?x:y;} int min(int x, int y){return x<y?x:y;}
int n, a, b, m, x, suma, delta[100005];
signed main(){read(n); read(x); read(a); read(b) ; read(m); suma = m - n*x + ((n*(n-1))/2)*b; if((suma)%(a+b)) return puts("-1"), 0; else suma/=(a+b); int xa = 2; while(suma){ while(suma < n-xa+1 && xa<=n) ++xa ; if(xa == n+1) return puts("-1"), 0; else delta[xa] = 1, suma -= n-xa+1, ++xa;}f(i,2,n) { if(delta[i]) delta[i] = delta[i-1] + a; else delta[i] = delta[i-1] - b;} f(i,1,n) printf("%lld ", delta[i]+x) ; puts(""); return 0; /*拜拜程序*/ }
T3

Input
Output
若无解,则输出”Impossible”。
否则第一行输出”Possible”,第二行输出 n 个正整数,依次输出序列 a 中每个数。
Data Constraint
解法
我们可以整理出一堆形如 \(xi − xj ≥ v\) 的式子。拓扑排序判环并求答案即可
注意到暴力连边级别是 \(O(n^2)\) 的。
不过我们可以建一些辅助点来优化一下状态,具体来说,先像线段树一样,每个点表示区间最大值,和子节点之间连长度为 \(0\) 的边。每次一个限制,先找到被 \(k\) 个点分割开的 \(k + 1\) 个区间,每个区间找到线树上对应的 \(O(log n)\) 个区间,然后新建一个点表示这些区间的最大值,与这些点连长度为 \(0\) 的边。最后 \(k\) 个点与这个点连长度为 \(1\) 的边。
这样的连边级别是 \(O(k log n)\) 的