可持久化数据结构

可持久化数据结构

总述

充分利用以前的状态

可持久化Trie树

这是一颗插入了"AFK"的可持久化Trie

接下来插入"KFC",此时新建一个根（因为要可持久化），然后我们来看他该怎么连边

• 首先，肯定要有"KFC"

• 其次，还要能访问到以前的节点

然后就可以这么搞：

然后插入"KFK"：

所以我们发现一个这样的算法：

ins(u,f) 被定义为一个插入算法

那么对于[a..z]中的字母X，考虑f所连的一条边权为X的边，若其存在，则将root[i]的X指针指向之。特别的，若X是要插入的字符串中正在处理的一位，则不执行以上操作，并将X指针指向一个新的节点，记该节点为t，该字符为m，该边所指向的节点为k

执行完后，递归ins(t,k)，把处理到的位置++

这样就好啦qwq

可持久化线段树

先建树，过程同普通线段树，不再赘述

然后假设建出来一颗这样的：

接下来修改v[1] = 3 ， 根据推理发现应该是这样的：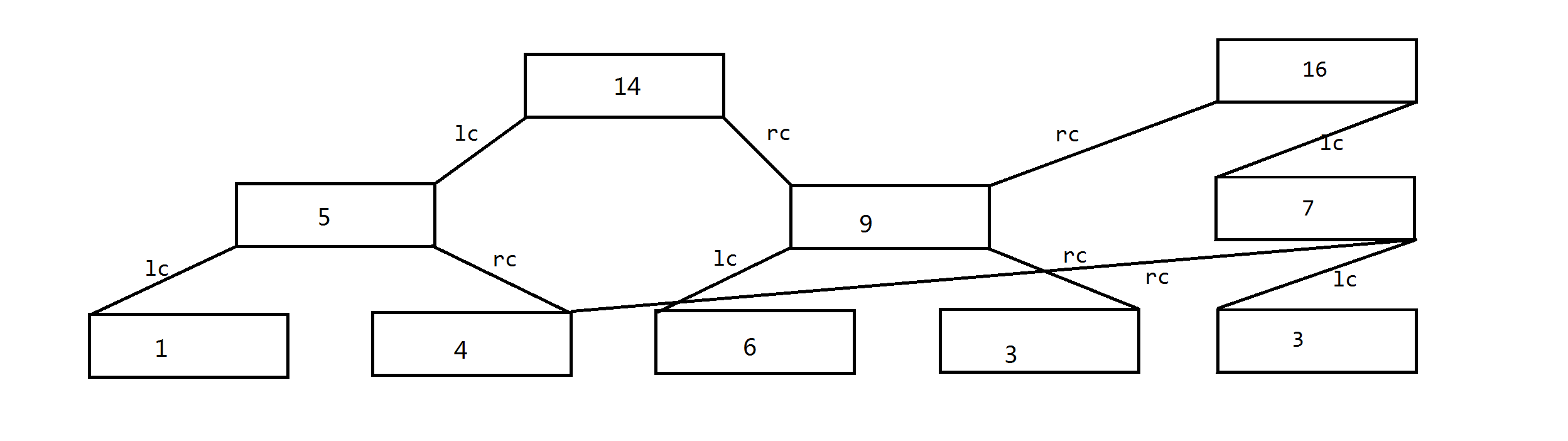

继续，v[2]=0，树长这样子：

OK，代码跟可持久化Trie+线段树样的，然后时间复杂度证明如下：

1.一开始树中只有原始的NlogN个节点
2.每次插入会增加一条长度为logN的链

所以总长度为O(NlogN+(N-1)logN)=O((2N-1)logN)=O(NlogN)