前端基础知识学习第三节
1.
JS实现快速排序
思路:选择一个值作为基础数,一般使用第一个值。快速排序算法的时间复杂度最差的情况是O(N2),平均时间复杂度是O(NlogN)
答案:
function quickSort(arr, begin = 0, end = arr.length - 1) {
if (begin > end) { // 跳出逻辑,从左向右查找下标不可能大于从右向左查找的下标
return;
}
let key = arr[begin]; // 初始值6
let i = begin; // 第一次下标对应值是6
let j = end; // 第一次下标对应值是8
let temp;
while (i != j) {
// 先从j开始向左查找,因为基数是最左边的第一个元素,直到找到第一个比基数小的元素停下来
while (i < j && arr[j] >= key) {
j --;
}
// 从i开始向右查找,直到找到第一个比基数大的元素停下来
// 这里一定要处理等于基数的情况,因为i是从第一个元素(基数)开始的
while (i < j && arr[i] <= key) {
i ++;
}
// 现在交换下标为i和j元素的位置
temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
// 上面的查找过程直到i == j停止,此时下标i对应的元素肯定小于基准数,不然要进行交换了,
// 接下来将i对应的元素和基准数交换,这样基准数左边都小于基准数,右边都大于基准数
// 其实回归一下刚才的过程,其实就是j要找小于基准数的元素,i要找大于基准数的元素,直到i和j相等为止
// 接下来我们继续处理左边的部分,处理的方式和上面一样,同样的道理右边的部分也是这么处理
// 所以这种场景下递归是最合适的
// 交换基数和i对应元素为止
arr[begin] = arr[i];
arr[i] = key;
quickSort(arr, begin, i - 1); // 左边部分
quickSort(arr, i + 1, end); // 右边部分
}
let arr = [6, 1, 2, 7, 9, 3, 4, 5, 10, 8];
quickSort(arr); // 代码执行结果:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2.
实现一个merge函数
let arr = [{ start: 1, end: 2 }, { start: 2, end: 3 }, { start: 5, end: 6 }, { start: 3, end: 5 }, { start: 8, end: 9 }];
输出结果:[{ start: 1, end: 6 }, { start: 8, end: 9 }]
arr.sort((a, b) => {
return a.start - b.start;
}).reduce((acc, cur) => {
if (acc) {
let last = acc[acc.length - 1];
if (cur.start <= last.end) {
last.end = cur.end;
} else {
acc.push(cur);
}
return acc;
}
return [cur]; // 初始化值为数组第一个元素
}, null);
3.
JS实现冒泡排序
思路:对数组中的元素两辆进行比较
答案:
function bubbleSort(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.ehgth - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
// let tmp = arr[j];
// arr[j] = arr[j + 1];
// arr[j + 1] = tmp;
[arr[j], arr[j + 1]] = [arr[j + 1], [j]]; // ES6数组解构实现数组元素交换,不申请额外变量空间
}
}
}
}
let arr = [68, 72, 29, 51, 45, 97, 68];
bubbleSort(arr); // 执行结果:[29, 45, 51, 68, 68, 72, 97]]
4.
Function.prototype.b = () => alert(1);
Object.prototype.a = () => alert(2);
function Foo() {};
var f1 = new Foo(); // 这里f1.__proto__指向Foo.prototype,Foo.prototype.__proto__指向Object.prototype, Object.prototype.__proto__指向null
f1.a(); // 打印2
f2.b(); // Object.prototype没有b方法,所以这里抛异常f1.b is not a function
附图:
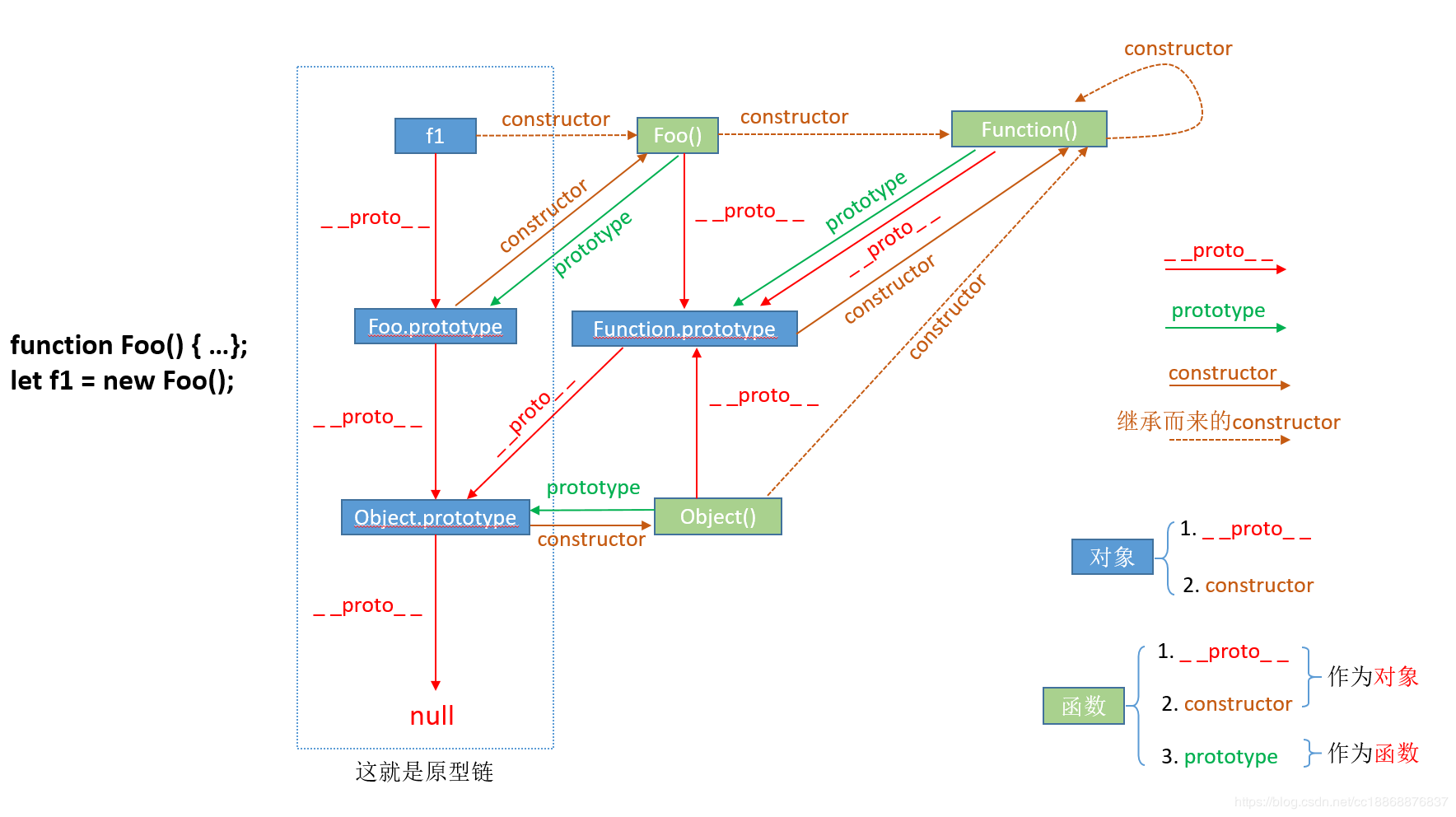
图片来自:https://blog.csdn.net/cc18868876837/article/details/81211729
5.
HTTP1/2/3,HTTPS?
HTTP是超文本传输协议,数据是明文传送,是处于TCP上层的协议,HTTP发的发展历程经过了HTTP1.0、HTTP1.1、HTTP2.0、HTTP3.0阶段,目前在使用较多的是
HTTP1.1、HTTP2.0,下面总结一下每个阶段的缺陷:
HTTP1.0:
缓存处理,HTTP1.0主要使用Expires来作为缓存判断的标准,这种方式有很大的问题,原因在于Expires控制缓存的原理是使用客户端的时间与服务
端返回的时间作对比,那么如果客户端与服务端的时间因为某些原因(例如时区不同,客户端与服务端有一方的时间不准确)发生误差,那么这种缓存控制的方式就失去
了意义
带宽优化及网络连接的使用,HTTP1.0中存在一些浪费贷款的现象,例如客户端只是需要某个对象的一部分,而服务端却将整个对象送过来了,并且不支持断点续传功能
HOST头处理,HTTP1.0中认为每台机器都绑定一个唯一的IP地址,因此请求头中没有传递主机名(hostname)
HTTP1.0不支持长连接,所以每次请求都要创建新的连接
HTTP1.1
HTTP1.1在HTTP1.0的基础上进行了一些优化,比如说通过Cache-Control更准确的进行了缓存处理、支持只请求资源的一部分(206 Partail Content)、新增了
更多的错误状态响应码、添加了请求/响应头HOST字段、支持开启长连接Connection: keep-alive;一定程度上弥补了HTTP1.0每次请求都要重新创建连接的缺点,
但是HTTP1.1的缺陷还是比较明显,高延迟-队头阻塞(Head-Of-Line Blocking)、明文传输-不安全、不支持服务端推送
HTTP2.0
HTTP2.0最大的目标是客户端和服务器只有一个连接,HTTP2.0相比HTTP1.1的改进有,
二进制传输,将请求和响应数据分隔为更小的帧并且他们采用二进制编码。
Header压缩,采用HPACK算法压缩头部,压缩率50%-90%,同时同一域名下的两个请求,只会发送差异数据,减少冗余的数据传输,降低开销。
多路复用,同一域名下的所有通信都在单个连接上完成,单个链接可以承载任意数量的双向数据流。
服务端推送,服务端可以新建“流”,主动向客户端发送消息,提前推送客户端需要的静态资源,减少等待的延迟。
提高了安全性,支持使用HTTPS进行加密传输。HTTP2.0的缺陷是,TCP以及TCP + TLS建立连接的延迟,TCP的队头阻塞没有彻底解决,
多路复用导致服务器压力上升,多路复用容易Timeout
HTTP3.0
改进的阻塞控制、可靠传输,快速握手,集成了TLS1.3加密,多路复用,连接迁移
参考:https://blog.csdn.net/Tencent_TEG/article/details/103966856
https://segmentfault.com/a/1190000020769188
https://www.jianshu.com/p/be29d679cbff
6.
前端性能优化有哪些方案?
1) HTTP部分
1.1 缓存控制,强制缓存、协商缓存
1.2 GZIP压缩
1.3 Cookies优化cookie体积以及合理设置cookie的路径和域名
1.4 减少HTTP请求数量CSS Sprites、图片Base64等
1.5 多域名分发解决浏览器并发下载资源限制
1.6 使用CDN
1.7 避免重定向和404
1.8 DNS预取
2) HTML
2.1 减少DOM操作
2.2 CSS放在head中引用,JS放在body结束位置
2.3 脚本延迟加载可以通过脚本的defer和async属性来异步加载脚本
2.4 减少使用iframe
3) CSS
3.1 开启GPU加速
3.2 文件合并、压缩
4) JS
4.1 事件委托
4.2 代码压缩
4.3 懒加载(路由懒加载)、预加载
7.
浏览器缓存原理
强制缓存
强制缓存就是向浏览器缓存查找该请求结果,并根据该结果的缓存规则来决定是否使用该缓存结果的过程强制缓存的情况主要有三种,
浏览器发起HTTP请求,首先查找浏览器缓存是否有该请求的缓存结果和缓存标示,如果没有,强制缓存失效,直接向服务器发起
请求(跟第一次向服务器发起请求一致)。如果存在该请求的缓存结果和缓存标示,但是该结果已失效,强制缓存失效,则向服务器发起请求(协商缓存)。
如果存在缓存结果和缓存标示,且该结果尚未失效,强制缓存生效,直接返回该结果。强制缓存的规则是:
当浏览器向服务器发起请求时,服务器会将缓存规则放入HTTP响应的响应头和请求结果一起返给浏览器,控制强制缓存的字段分别是Expires和Cache-Control,
其中Cache-Control优先级比Expires高,两个一起使用时候Cache-Control会覆盖Expires
Expires是HTTP1.0引入的,缺陷比较明显,比如在浏览器和服务器时间有误差时候,就不能准确的进行判断
Cache-Control是HTTP1.1引入的,主要取值为,
public: 所有内容都将被缓存(客户端和代理服务器都可缓存)
private: 所有内容只有客户端可以缓存,Cache-Control的默认值
no-cache: 客户端缓存内容,但是否使用缓存则需要经过协商缓存来验证决定
no-store: 所有内容都不会被缓存,即不使用强制缓存,也不使用协商缓存
max-age: 缓存内容将在设置的秒数后失效
协商缓存
协商缓存就是强制缓存失效后,浏览器携带缓存标示向服务器发起请求,由服务器根据缓存标示决定是否使用缓存的过程,主要有两种情况,
协商缓存生效,返回304
协商缓存失效,返回200和请求结果
协商缓存的标示也是在HTTP响应的响应头和请求结果一起返回给浏览器的,控制协商缓存的字段有:Last-Modified/If-Modified-Since和Etag/If-Node-Match,
其中Etag/If-Node-Match的优先级比Last-Modified/If-Modified-Since高
参考:https://juejin.im/entry/5ad86c16f265da505a77dca4
8.
var obj = { a: 1 };
function fun(obj) {
obj.b = 1;
obj = { a: 2 };
obj.b = 2;
}
fun(obj);
console.log(obj);
答案:{ a: 1, b: 1 }
分析:
调用函数fun(obj);时候传递的参数obj是引用类型,引用类型传递的是引用,所以obj.b = 1; 执行之后函数外边的obj是{ a: 1, b: 1 },
接下来对函数传进来的参数obj进行了重新赋值,此时函数内部的obj指向了{ a: 2 },与函数外部的obj没有了关系,然后代码又继续对
函数内部的obj添加属性b等于2的操作,所以函数执行完外部的obj是{ a: 1, b: 1},函数内部的obj是{ a: 2, b: 2 }
9.
defer和async的作用和区别
defer:
作用:用于开启新的线程下载脚本文件,并使脚本在文档解析完成后执行
区别:
1) defer只适用于外联脚本,如果script标签没有指定src属性,只是内联脚本,不要使用defer
2) 如果有多个声明了defer的脚本,则会按顺序下载和执行
3) defer脚本会在DOMContentLoaded和load事件之前执行
async:
作用:用于异步下载脚本文件,下载完成后立即解释执行代码
区别:
1) 只适用于外联脚本,这一点和defer一致
2) 如果有多个声明了async的脚本,其下载和执行也是异步的,不能确保彼此的先后顺序
3) async会在load事件之前执行,但并不能确保和DOMContentLoaded的执行先后顺序
10.
用方法实现 n!
首先会考虑到最简单的递归实现
function factorial(n) {
if (n <= 1) {
return 1;
}
return n * factorial(n - 1);
}
// factorial(5); 结果:120
使用尾调用优化方式来实现:
function factorial2(n, result = 1) {
if (n <= 1) {
return result;
}
return factorial(n - 1, n * result);
}
11.
有这样一个数组[5, 6, 8, 5, 7, 3, 4, 9],对于每一个元素如果后面的元素比自己大,那么返回第一个比自己大的元素,否则返回-1
function getFirstGreatNum(arr) {
let ret = [];
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] > arr[i]) {
ret.push(arr[j]);
} else {
ret.push(-1);
}
break;
}
}
ret.push(-1); // 最后一个元素
return ret;
}
这种方法的时间复杂度是O(n)平方,优化的方案是
12.
判断一个数组中是否存在元素出现次数大于其他元素?
答案:
// 一次遍历从数组中删除n个不同的元素,如果数组的长度不等于0则表示存在元素出现次数大于其他元素
function isExist(arr) {
let clone = arr.slice(0);
let tmp = {};
for (let i = clone.length - 1; i >= 0; i--) {
let cur = clone[i];
if (!tmp[cur]) {
clone.splice(i, 1);
tmp[cur] = 1;
}
}
// 如果数组clone长度大于0则说明有出现多次的元素
return clone.length ? true : false;
}
let arr = [6, 1, 2, 7, 9, 3, 4, 5, 3, 3, 2];
isExist(arr); // true



 浙公网安备 33010602011771号
浙公网安备 33010602011771号