树，二叉树，查找

一，树，二叉树，查找（初步学习，如有不足，烦请告知）

一：思维导图

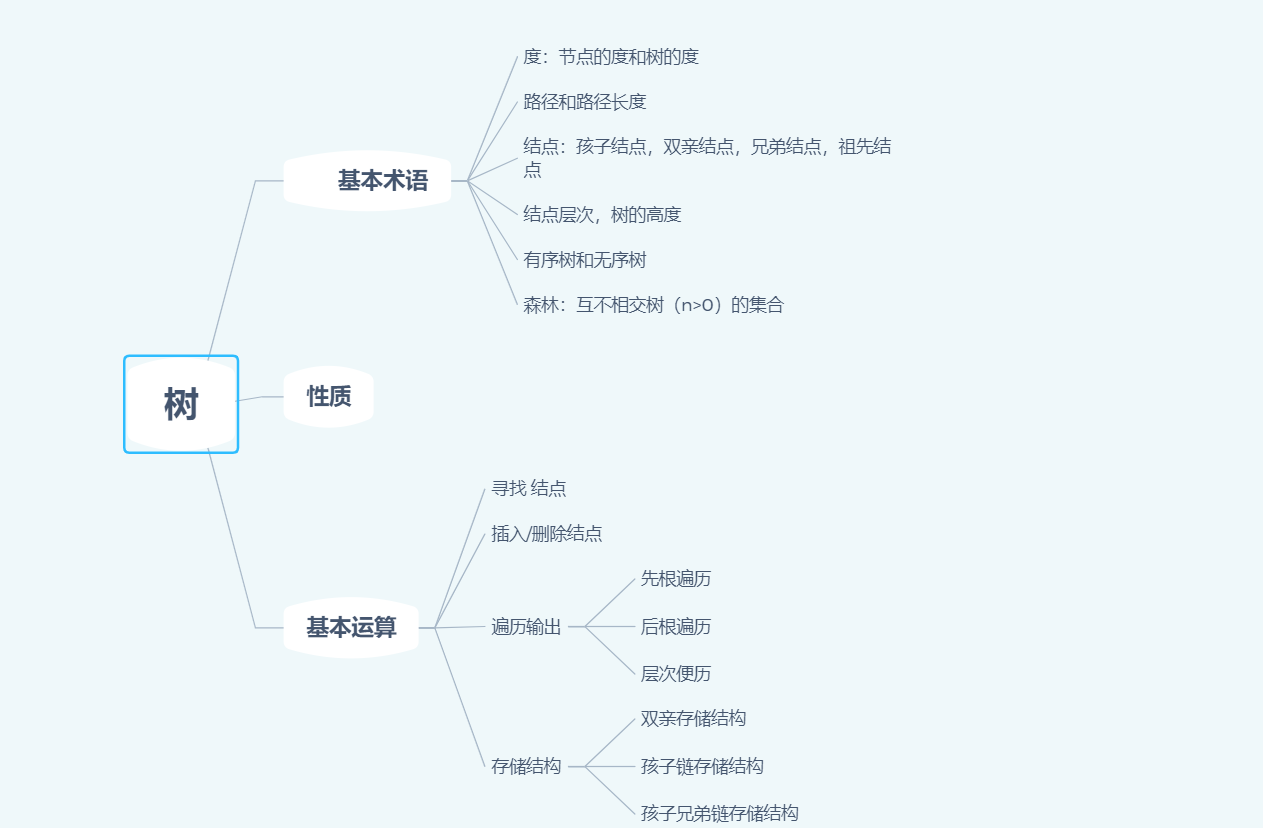
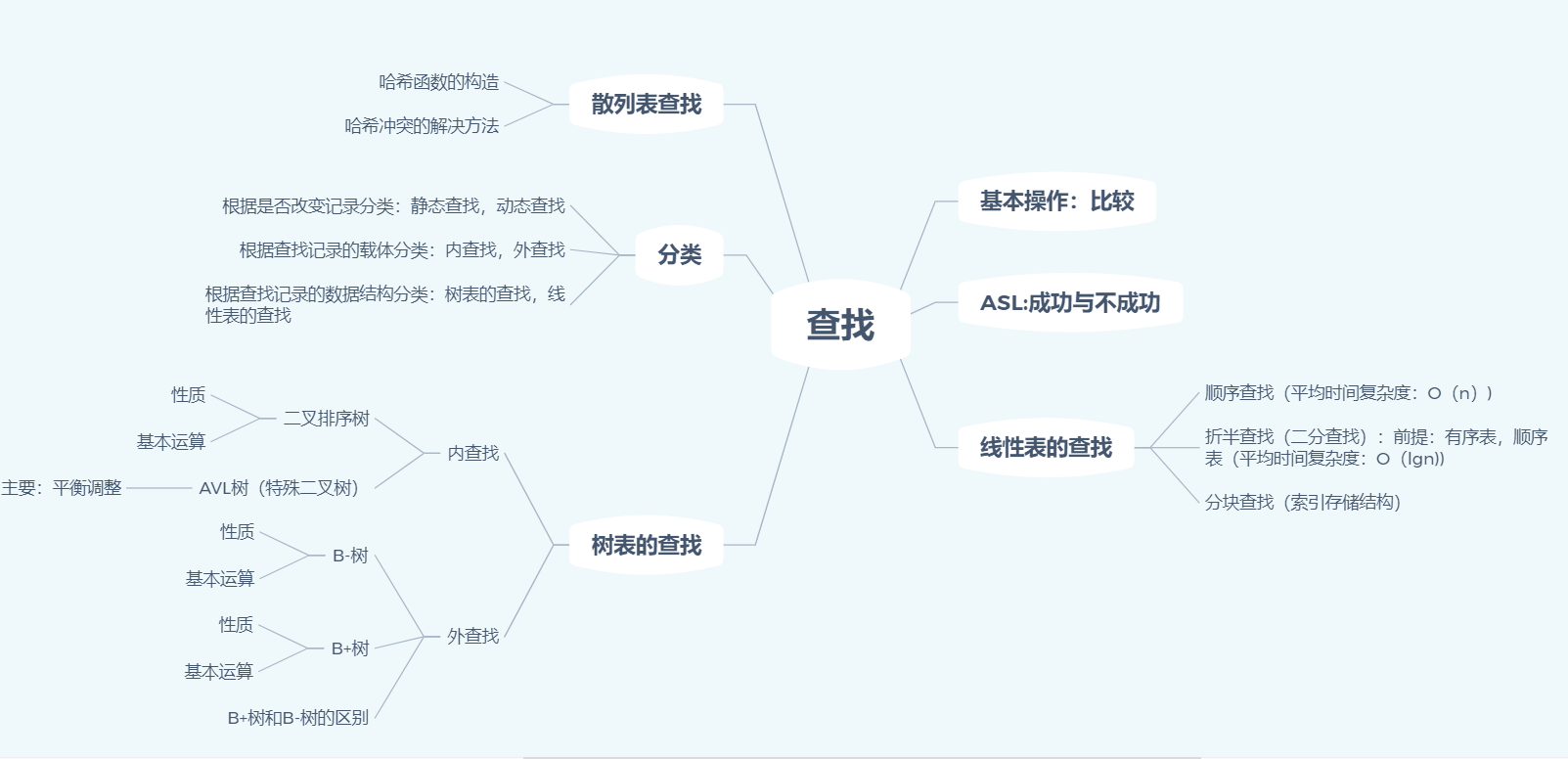
联系：

树与二叉树可以相互转换
查找中的树表查找;就是利用了二叉树，降低了时间复杂度

二：概念

1. 树

基本术语：
1. 度：
  1. 节点的度：节点的分支数
  2. 树的度：树中节点的最大分支数
树的性质：
1. 树的节点数=所有节点的度+1（总结点数=分支数+1）
2. 度为m的树的第i层最多有m^(i-1)（i>=1）个节点
3. 高度为h的m次数最多有(m^h-1)/(m-1)个节点
4. 具有n个节点的m次树的最小高度为⌈logm (n(m-1)+1)⌉
树的基本运算：
1. 树的先根遍历：访问根节点，再按照从左到右的顺序先根遍历每一棵子树
2. 树的后根遍历：按照从左到右的顺序后根遍历每一棵子树，再访问根节点

2. 二叉树

定义：递归定义，度最多为2
性质：
1. 在二叉树的第i层上组多有2^(i-1)个节点（i>=1)
2. 深度为h的二叉树最多含有2^h-1个节点
3. n0=n2+1
三个特殊二叉树
1. 满二叉树：深度为k,含有2^k-1个节点
2. 完全二叉树：树中n个节点，节点的编号依次与满二叉树中一一对应
  1. 任意一个编号为i的节点
    1. 若i=1,为根节点，否则编号为i/2为其双亲节点
    2. 若2i>n,该节点无左孩子，否则，编号为2i的节点为左孩子
    3. 若2i+1>n,该节点无左孩子，否则，编号为2i+1的节点为右孩子
  2. 具有n(n>0)个节点的完全二叉树的高度为：⌈log2 (n+1)⌉或者⌈log2 (n+1) ⌉
3. 偏二叉树（单支树）

二叉树的构造

根据中序序列和前序序列：前序序列确定根，中序序列确定左右子树
根据后序序列和中序序列：后序序列确定根，中序序列确定左右子树

根据顺序数列构造链式二叉树：

Node GreatTree(string s, int  i) {
    if (i > s.size()-1) {
        return NULL;
    }
    if (s[i] == '#') {
        return NULL;
    }
    Node root = new treeNode;
    root->Data = s[i];
    root->lchild = GreatTree(s, i * 2);
    root->rchild = GreatTree(s, i * 2 + 1);
    return root;
}

根据先序序列

BiTree Create(string str,int &i) {
    if (i > str.size() - 1) {
        return NULL;
    }
    else if (str[i] == '#') {
        return NULL;
    }
    else {
        BiTree T = new BiTNode;
        T->ch = str[i];
        T->lchild = Create(str, ++i);
        T->rchild = Create(str, ++i);
        return T;
    }

}

树、二叉树和森林的转换
1. 树转为二叉树：用孩子-兄弟存储法
2. 森林转为二叉树：第一棵树提供左子树和根节点，每一棵树用树转为二叉树的方法
3. 二叉树转为树、森林：上述做法的逆运算
特殊构造的二叉树：
1. 线索二叉树
  1. 当我们通过中序线索二叉树输出中序序列时：当我们找第一个节点时，该节点为最左下节点
2. 哈夫曼树(带权路径最小)
  1. 构造方法：找还没参与过构造的最小和次小节点构造，当参与构造序列中所有元素参与构造，构造结束

3. 查找

树表查找：
1. AVL树（bf<=1)的二叉排序树
2. B-树和B+树：
  1. 主要运用于外存
哈希表的查找：
1. 哈希表的构造：
  1. 除留余数法：
    
    h(k)=m%p(p为素数，p<=m)
2. 哈希冲突的解决方法：
  1. 拉链法：所有有冲突的元素在一条链表上
  2. 开放定址法:
    1. 线性探测法：
      1. d0=h(k);
      2. di=(di-1)mod p;
    2. 平方探测法：
      1. d0=h(k);
      2. di=(d0+-i^2) mod p;

三，小问号+小思考

1.二叉树的非递归算法（主要学习了一下课本，有更好的想法时会回来改）

现在我们有一棵树（问题）

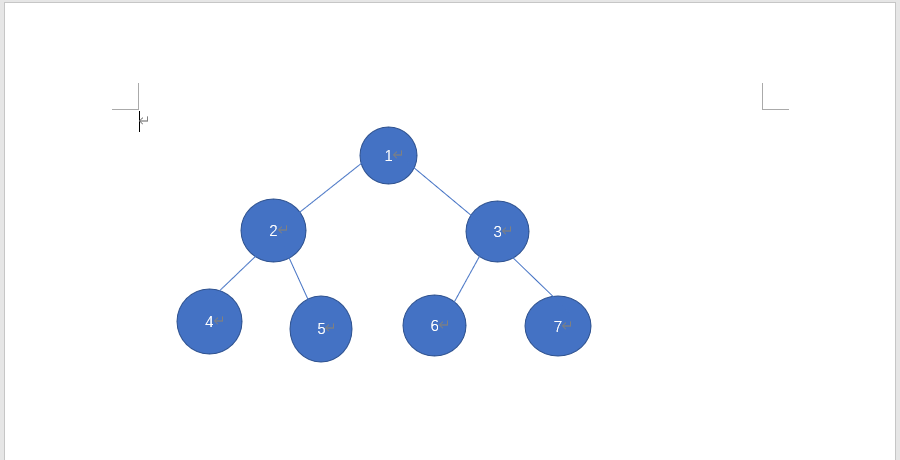
我们可以轻易看出它的先序输出序列为：1 2 4 5 3 6 7，中序输出序列为 4 2 5 1 6 3 7，后序输出序列为 4 5 2 6 7 3 1,怎样非递归对它进行先/中/后序非递归遍历（当我们需要用非递归算法时，我们需要一个存储结构存储中间状态，我们选用了栈）

1. ```
void PreOrder(Bitree T) {//先序遍历非递归算法
    stack<Bitree>st;
    Bitree q;
    if (T) {
        st.push(T);
        while (!st.empty()) {
            q = st.top();
            cout << q->data << " ";
            st.pop();//访问并出栈每次部分二叉树的根节点
            if (q->rchild != NULL) {//先将右孩子进栈
                st.push(q->rchild);
            }
            if (q->lchild != NULL) {
                st.push(q->lchild);
            }
        }
    }

}
```
2. 部分实例分析（先序输出序列为：1 2 4 5 3 6 7）：
  1. 由于树不空，我们将根节点进栈，我们将1进栈，访问并出栈1，现在我们已经输出了1;
  2. 之后我们将3先进栈（3为根节点1的右子树的根节点，由于栈先进后出，右孩子比左孩子先进栈，先进后处理），然后我们将2进栈，与递归操作相似，2为根节点1的左子树的根节点，再对2进行出栈访问，进栈2的右孩子，进栈2的左孩子
  3. 在栈不为空的时候，循环操作
1. ```
void InOrder(Bitree T) {
    stack<Bitree>st;
 while (!st.empty() || T) {
        while (T) {
      st.push(T);
            T = T->lchild;//将根节点和左孩子依次进栈
     }
        if (!st.empty()) {
         T = st.top();
            st.pop();
            cout << T->data << ' ';
            T = T->rchild;//处理右子树
     }
    }

}
```
2. 对于非递归中序遍历，先将根和左下节点进栈，依次访问出栈，并处理右子树，循环以上操作，
3. 部分实例分析(中序输出序列为 4 2 5 1 6 3 7)：
  1. 我们先将1,2,4都进栈，相当于我们定位到最左边的子树的根节点4，然后我们出栈并访问4，相当于输出顺序中的“左”，现在已经输出4
  2. 由于4没有右孩子处理，我们将出栈并访问2，相当于输出顺序中的“根”，截止现在输出 4 2
  3. 我们对5进栈处理，由于5没有左孩子，我们出栈并访问5，相当于输出序列的“右”，截止现在输出 4 2 5……

void PostOrder(Bitree T) {
    Bitree r=NULL;//用来作为前驱
 int flag = 1;//标记栈顶节点是否已处理了右子树
    stack<Bitree>st;
 do {
        while (T) {
         st.push(T);
            T = T->lchild;//将T所有的左下节点进栈
     }
        r = NULL;//在每一个栈顶节点还未处理前值为NULL
        flag = 1;
        while (!st.empty()&&flag) {
            T = st.top();
            if (r == T->rchild) {//此时以T为根节点的树左右孩子均已处理
                cout << T->data << " ";
                r = T;//r标记前一个处理节点
                st.pop();

            }
            else {
                T = T->rchild;//处理该节点的右孩子
                flag = 0;//此时不应该处理栈顶节点
            }

        }
    } while (!st.empty());

}

对于非递归后序遍历：我们对于根节点只有在左右子树都访问过的时候，才访问。每一次的栈顶节点相当于每一个部分树的根节点，我们就需要一个指针和标记（标记当前栈顶节点的左右子树是否已访问），确定是否访问栈顶节点
部分实例分析(后序输出序列为 4 5 2 6 7 3 1)：
1. 我们先将1,2,4都进栈，此时栈顶元素为4，4没有右孩子，出栈访问4，现在已经输出4；
2. 此时栈顶元素为2，2的右孩子5还没有被处理，则先处理5，将5进栈，由于5没有左右孩子，访问并出栈5 ，截止现在输出了4 5；
3. 2 的右孩子5已被处理，则将2 出栈并访问，截止现在输出了 4 5 2……

2. 排序树的删除节点（针对被删除节点有左右子树的情况）

之前我的解决方法

void Delete1(Bitree &p, Bitree& l) {//删除节点有左右子树，找删除节点的左子树中最大的节点，替换它
	Bitree q;
	if (l->rchild != NULL) {
		Delete1(p, l->rchild);//找删除节点的左子树中最大的节点,即前继节点
	}
	else {
		p->key = l->key;
		q = l;
		l = l->lchild;
		delete (q);
		
	}
}

在pta中和别人学习到的一种,算是调用自身，我觉得挺好玩的

BinTree Delete(BinTree BST, ElementType X) {
    if (!BST) {
        printf("Not Found\n");
    }
    else if (X > BST->Data) {
        BST->Right = Delete(BST->Right, X);
    }
    else if (X < BST->Data) {
        BST->Left = Delete(BST->Left, X);

    }
    else {
        if (BST->Left && BST->Right) {
            BinTree p = FindMin(BST->Right);//BinTree p = FindMax(BST->Left);
            BST->Data = p->Data:
            BST->Right = Delete(BST->Right, BST->Data);//BST->Left = Delete(BST->Left, BST->Data);
        }
        else {
            if (!BST->Left) {
                BST = BST->Right;
            }
            else if (!BST->Right) {
                BST = BST->Left;
            }
        }
    }
    return BST;
}

3. 稍微复杂的AVL平衡（刚开始的时候，我更倾向于超星上的插入，不过我在这里用的是旋转）

先让我举个例子（取自ppt）

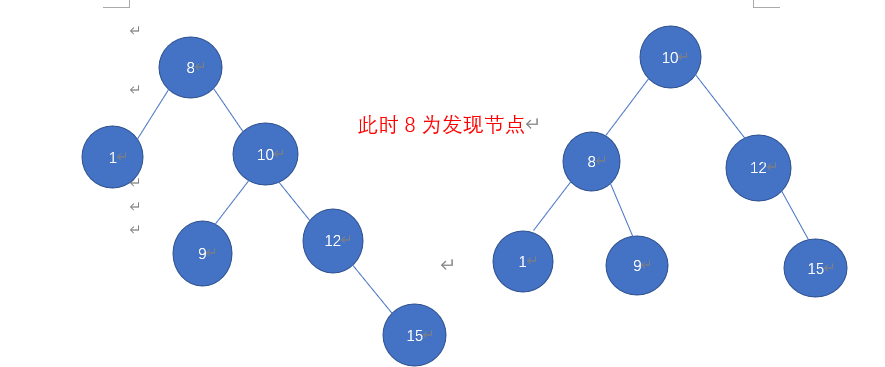
插入8 12 1 10 15 9时
1. 我们确定发现节点为8，将发现节点8和离插入节点9最近的两个节点进行重排，其他节点先不变，将RL型转为RR型，再逆时针旋转
2. 将RL型转为RR型

3. AVl树的一些计算（由于课上讲的较少）

先让我举个例子（来自课堂派）

若AVL树的深度为6,（空树的深度为0，只有一个节点的深度为1），求问此时AVL树的最少节点为多少？
1. 设每棵树的深度为h，深度为h的树的最少节点为Min(h)
2. Min(0)=0,Min(1)=1,Min(2)=2,Min(3)=Min(1)+Min(2)+1,我们可以得出Min(h)=Min(h-1)+MIn(h-2)+1(h>=2);
3. 文字版规律叙述：原理是AVl树的每棵部分树都是AVL树，就一颗深度为h的AVL树为根节点和左子树、右子树组成（根节点在这种情况不影响平衡因子），节点最少的情况为，当左子树（右子树）看成深度为h-1的AVL树，当右子树（左子树）看成深度为h-2的AVL树，Min(h)=Min(h-1)+MIn(h-2)+1(h>=2);
4. 图画版规律叙述（我就举几个情况）：

4. B-树节点的删除（节点插入的逆运算，课上没咋讲，是的，没错，它不能直接删除）

先让我举个例子（来自作业）的3阶B-树

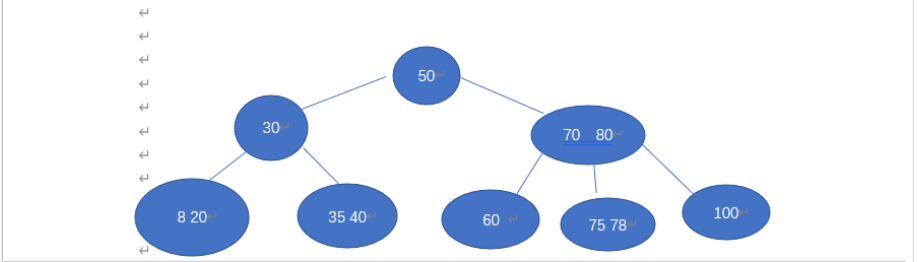
我们要先删除节点100，再删除节点60

让我们开始搞
1. 先熟悉一下B-树删除一个节点原理
  
  原理：非根节点的关键字个数不能少于⌈m/2⌉-1,否则
  1. 若被删除关键字所在节点为非叶子节点，找后继节点替代，后继节点肯定为叶子结点，然后就转为删除叶子节点中的关键字的问题
  2. 删除的关键字在叶子结点
    1. 若删除关键字所在的节点关键字>⌈m/2⌉-1,直接删除该关键字
    2. 当左/右兄弟中关键字富余，从左/右兄弟中调用一个关键字，再删除关键字
    3. 进行节点合并（将双亲节点中下移一个关键字，与被删除节点和相邻兄弟节点合并），再删除关键字
1. 1. 删除100
    
    删除后
  2. 删除60
    1. 还没删除前是这样
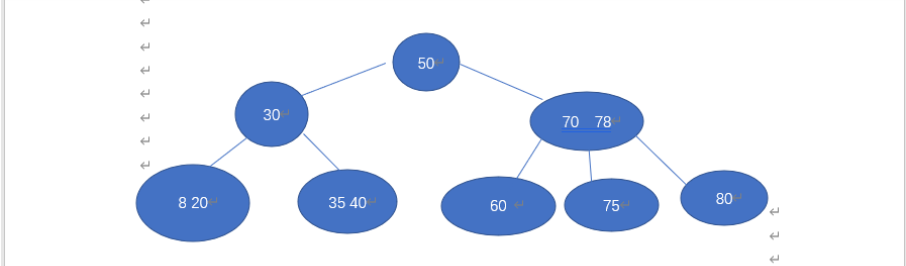
    1. 我们发现60的兄弟节点的关键字不富余，我们则要进行节点合并
    删除后

5. 哈希函数中AVL不成功的计算

让我们先举个例子，题目来自课堂派

让我们先了解一下这时候的不成功是什么情况：

本题哈希函数，我们记为h(key)=key%p我们得到的值记为d0=h(hey),若我们发现d0所在地址的关键字与我们查找的关键字不同，我们向di=(di-1 +1)%p(本题p为11)查找，直到当我们找到的地址里啥也没有(可能出现折返查找的情况(因为我们进行了取余操作))，我们才灰心丧气，查找不成功，注意：由于我们没有进去比对的话，我们不知道里面没关键字，所以找到空也记为1次
不成功情况为11，就某数%11肯定是共有11种情况（0~10）
让我们再举个例子，还是来自课堂派
1. 不成功情况为找到空指针：此时空指针的话，我们要查找的数就没有进去比对的存储空间，因为为空，所以我们找到空指针时不记次数

posted @ 2020-04-25 10:42 rghli(林洁颖) 阅读(203) 评论(0) 编辑收藏举报

刷新页面返回顶部

rghli