字符串border原理小结&KMP优化
字符串 \(s\) 的border：若 \(s\) 的一个子串既是它的前缀又是它的后缀，则这个子串是它的border（一般不包含本身）
字符串 \(s\) 的period：循环节。用前 \(T\) 个字符向后不断复制，能得到 \(s\)，最后一次可以只复制一部分
引理1：如果有一个border \(k\) 长度大于 \(s\) 的一半，可以得出得 \(s\) 有周期 \(|s|-|k|\)
同时，中间重叠部分是一个border，绿色部分构成了一组等差数列border：
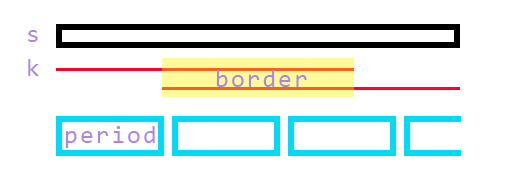
前 \(T\) 个字符是周期的话，后 \(T\) 个显然也是周期：
当然，这些都不重要
引理2：如果 \(p,q\) 都为周期，则 \(gcd(p, q)\) 也为周期
感性理解非常显然，证明同样不难，不做赘述了
引理3：字符串 \(s\) 所有不小于 \(|s|\) 一半的border构成一个等差数列
显然有\(|s|-|u|\) 为最小周期，能组成一个公差为 \(|s|-|k|\) 的等差数列；
证明不存在这个等差数列之外的border：
假设 \(u\) 是字符串的最大border，设另一个不小于 \(|s|\) 一半的border为 \(v\)
由引理1，2可得，\(gcd(|s|-|u|,|s|-|v|)\) 是一个周期，而 \(|s|-|u|\) 已经是最小周期了，所以 \(|s|-|v|\) 为最小周期的整数倍，得证。
引理4：可以把字符串分成 \(log|s|\) 段，每一段的border都是一个等差数列
引理3的扩展，建议先看下面的应用，再回来就很好理解了。
先把 \(s\) 分成两半，由引理3，右边的border是等差数列（这里的border指：以右边点为终点的前缀作为border）
左边的border呢？再拆成一半，新的右半边又构成了等差数列。。。
所以一个字符串的所有border可以被我们分成log数量级个等差数列。
应用：为什么要考虑border中的等差数列？
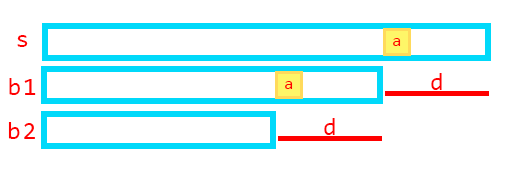
如图所示，\(s\) 的所有成等差数列的border，其下一位一定相同
在KMP匹配中，我们可以利用这个性质快速跳过一串border
具体而言，在一次跳border时，如果发现border长度不小于原串的一半，则接下来的border构成等差数列，直到一半以下（引理3）
可以直接跳到 \((x-(x/2/d)*d)\) 处，即比一半大的第一个位置（整除）
（网上博客直接跳到了 \(x\%d+d\) 处，经过几道题检验也是对的，但不是很能理解）
一次至少跳一半，保证 \(log\) 次以内可以跳完
\(\quad\)
标解是建树后LCA，我们这个稳定跳log次border的“暴力匹配”可以更优雅地过这个题
int n, m;
string s;
int nt[maxn];
void get_next(){
nt[1] = 0;
for(int i=2;i<=n;i++){
int p = nt[i-1];
while(p && s[p+1] != s[i]) p = nt[p];
if(s[p+1] != s[i]) nt[i] = 0;
else nt[i] = p + 1;
}
}
void solve() {
cin >> s; n = s.size();
s = '0' + s;
get_next();
cin >> m;
while(m--){
int x, y; cin >> x >> y;
x = nt[x], y = nt[y];
while(x != y){
if(x < y) swap(x, y);
if(nt[x] > x/2){
int d = x - nt[x];
if(y % d == x % d) x = y;
else x = x - (x/2/d) * d;//大优化
}else x = nt[x];
}
cout << x << '\n';
}
}
\(\quad\)
例题：2021ICPC沈阳站M
当前位置的答案即为上一位置的答案的某个border加上新字符；找到最小的 加上新字符后大于原答案的border即可。（有一定难度，具体见题解）
int n, m;
string s;
int nt[maxn];
int head = 0;
void expend_nt(int frm, char c){
if(frm == 0){
nt[frm+1] = 0;
return;
}
int p = nt[frm];
while(p && s[head+p+1] != c) p = nt[p];
if(s[head+p+1] != c) nt[frm+1] = 0;
else nt[frm+1] = p + 1;
}
void solve() {
cin >> s; n = s.size();
s = '0' + s;
nt[1] = 0;
cout << "1 1\n";
int lst = 1;
for(int i=2;i<=n;i++){
int x = lst, len = lst + 1;
while(x > 0){
if(s[i] > s[i-lst+x]) len = x + 1;
if(nt[x] > x/2){
int d = x - nt[x];
x = x % d + d;
}else x = nt[x];
}
if(s[i] > s[i-lst]) len = 1;
head = i - len;
expend_nt(len-1, s[i]);
lst = len;
cout << i-len+1 << ' ' << i << '\n';
}
}
