珂朵莉树（ODT）
前言
主要是一种暴力思想。。。
本文来自 wiki 与洛谷题解的整合。
应用
主要是应付随机数据（区间操作）
实现
有几个核心操作。
set实现方法
定义
struct node
{
intt l,r;//intt:long long
mutable intt v;
node(const intt &ll,const intt &rr,const intt &vv) : l(ll),r(rr),v(vv) {}
bool operator <(const node &o)const
{
return l<o.l;
}
};
set<node>odt;
split 操作（分裂）
auto split(int x)
{
auto it=odt.lower_bound(node(x,0,0));
if(it!=odt.end()&&it->l==x)return it;
it--;
intt l=it->l,r=it->r,v=it->v;
odt.insert(node(l,x-1,v));
return odt.insert(node(x,r,v)).first;
}
- 如果分裂的点恰好是某个区间的左端点，就不用分裂，保留即可。
- 如果分裂的点在一个区间的中间节点，就将其分为 \([l,x-1]\) 和 \([x,r]\) 这两个区间
- 注意：
odt.insert(node(x,r,v)).first这表示新加入的node的位置的迭代器（这是因为insert返回了一个pair，first就只新加入的node的位置的迭代器了）
assign 操作（区间推平）
void assign(intt l,intt r,intt v)//intt:long long
{
auto itr=split(r+1),itl=split(l);
//注意:一定得是这个顺序split，因为，如果先分裂l,那么有可能会发生itl指向的是一个原来的迭代器，然而原来的迭代器已经被删除了，那么就 RE 了
odt.erase(itl,itr);
odt.insert(node(l,r,v));
}
将边角余料分裂出来，再将中间所有元素删除，最后加入推平区间。
如下图：
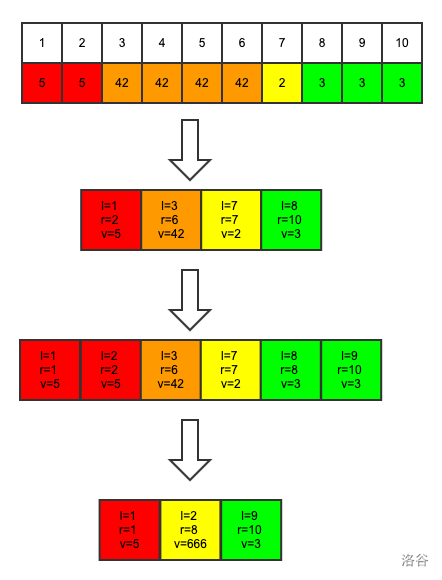
set的一个用法：erase(first,last)删除迭代器在 \([first,last)\) 范围内所有元素。
add 操作（区间加）
找到每一个段，暴力修改
void add(intt l,intt r,intt v)
{
auto itr=split(r+1),itl=split(l);
for(auto it=itl;it!=itr;it++)
{
it->v+=v;
}
}
例题
贴海报
简化题意：区间推平。。。
直接写！！！
#include <bits/stdc++.h>
using namespace std;
const int N=1e7+5;
int n,m;
struct node
{
int l,r;
mutable int v;
node(const int &l,const int &r=-1,const int &v=0) : l(l),r(r),v(v){}
bool operator <(const node &o) const
{
return l<o.l;
}
};
set<node>odt;//珂朵莉树
set<node>::iterator split(int pos)
{
auto it=odt.lower_bound(node(pos,0,0));
if(it!=odt.end()&&it->l==pos)return it;
it--;
int l=it->l,r=it->r,v=it->v;
odt.erase(it);
odt.insert(node(l,pos-1,v));
return odt.insert(node(pos,r,v)).first;
}
void assign(int l,int r,int x)
{
set<node>::iterator itr = split(r + 1), itl = split(l);
odt.erase(itl,itr);
odt.insert(node(l,r,x));
}
bool vis[1005];
int main()
{
cin>>n>>m;
odt.insert(node(1,n,0));
for(int i=1;i<=m;i++)
{
int l,r;
cin>>l>>r;
assign(l,r,i);//区间推平
}
int res=0;
auto itr=split(n+1),itl=split(1);
for(;itl!=itr;itl++)//统计个数
{
if(!vis[itl->v]&&itl->v>0&&itl->v<=m)
{
vis[itl->v]=1;
res++;
}
}
cout<<res;
return 0;
}
CF896C
简化题意：支持以下操作
- 区间加
- 区间推平
- 区间第 \(k\) 小
- \(\sum_{i=l}^{r}a[l]^x\pmod p\)
前面两个比较简单，主要是后面的。
第3个：暴力排序
第4个：暴力枚举，快速幂求解
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
ll n,m,seed,mx;
ll a[N];
inline ll rnd()
{
ll t=seed;
seed=(seed*7+13)%1000000007;
return t;
}
struct node
{
ll l,r;
mutable ll v;
node(const ll &l,const ll &r,const ll &v) : l(l),r(r),v(v) {}
bool operator< (const node &o) const
{
return l<o.l;
}
};
set<node> s;
set<node>::iterator split(int x)
{
set<node>::iterator it=s.lower_bound(node(x,0,0));
if(it!=s.end()&&it->l==x)return it;
it--;
if(it->r<x)return s.end();
ll l=it->l,r=it->r,v=it->v;
s.erase(it);
s.insert(node(l,x-1,v));
return s.insert(node(x,r,v)).first;
}
inline void add(ll l,ll r,ll x)
{
set<node>::iterator itr=split(r+1),itl=split(l);
for(;itl!=itr;itl++)
{
itl->v+=x;
}
}
inline void assign(ll l,ll r,ll x)
{
set<node>::iterator itr=split(r+1),itl=split(l);
s.erase(itl,itr);
s.insert(node(l,r,x));
}
inline void rk(ll l,ll r,ll x)
{
set<node>::iterator itr=split(r+1),itl=split(l);
vector<pair<ll,ll>>a;
for(;itl!=itr;itl++)
{
a.push_back(make_pair(itl->v,(itl->r-itl->l+1)));
}
sort(a.begin(),a.end());
for(int i=0;i<a.size();i++)
{
ll t=a[i].second;
if(t<x)
{
x-=t;
}
else
{
cout<<a[i].first<<'\n';
break;
}
}
}
inline ll qmi(ll x,ll y,ll p)
{
ll res=1;
x%=p;
while(y)
{
if(y&1)res=(res*x)%p;
y>>=1;
x=(x*x)%p;
}
return res;
}
inline void pw(ll l,ll r,ll x,ll y)
{
set<node>::iterator itr=split(r+1),itl=split(l);
ll sum=0;
for(;itl!=itr;itl++)
{
sum=(sum+(itl->r-itl->l+1)*qmi(itl->v,x,y)%y)%y;
}
cout<<sum<<'\n';
}
int main()
{
cin>>n>>m>>seed>>mx;
for(int i=1;i<=n;i++)a[i]=(rnd()%mx)+1;
int l=1;
for(int i=2;i<=n;i++)
{
if(a[i]!=a[i-1])
{
s.insert(node(l,i-1,a[i-1]));
l=i;
}
}
s.insert(node(l,n,a[n]));
for(ll i=1,op,l,r,x,y;i<=m;i++)
{
x=0,y=0;
op=(rnd()%4)+1;
l=(rnd()%n)+1;
r=(rnd()%n)+1;
if(l>r)swap(l,r);
if(op==3)x=(rnd()%(r-l+1))+1;
else x=(rnd()%mx)+1;
if(op==4)y=(rnd()%mx)+1;
if(op==1)
{
add(l,r,x);
}
if(op==2)
{
assign(l,r,x);
}
if(op==3)
{
rk(l,r,x);
}
if(op==4)
{
pw(l,r,x,y);
}
}
return 0;
}
