概率论

概率论

基本概念

概率空间

我们将三元组 \((\Omega,\mathcal{F},P)\) 称为一个概率空间，其中，\(\Omega\) 指样本空间（指明随机现象所有可能出现的结果） ，\(\mathcal{F}\) 指事件域（我们所关心的所有事件），\(P\) 概率函数（描述每一个事件发生的可能性大小）。

概率函数的性质

对于任意随机事件 \(A,B\in \mathcal{F}\) ，有

• 单调性：若 \(A \subset B\)，则有 \(P(A)\le P(B)\)
• 容斥原理：\(P(A+B)=P(A)+P(B)-P(AB)\)
• \(P(A-B)=P(A)-P(AB)\)

条件概率

\[P(A|B)=\frac{P(AB)}{P(B)} \]

其中，\(P(A|B)\) 表示在 \(B\) 发生的前提下，\(A\) 发生的概率（条件概率），\(P(AB)\) 表示 \(AB\) 同时发生的概率，\(P(B)\) 发生的概率。

证明：

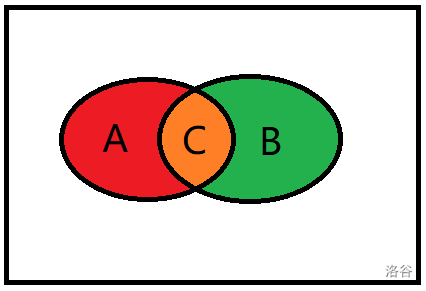
将概率转换成一张图（概率空间），那么设 \(P(A)=A+C,P(B)=B+C,P(AB)=C\).

因为 \(P(A|B)\) 表示 表示在 \(B\) 发生的前提下，\(A\) 发生的概率，

所以总共的情况就是 \(P(B)\)，在 \(B\) 发生的前提下，\(A\) 发生情况就是 \(P(AB)\).

由于概率等于事件的基本结果数除以所有可能出现的基本结果的总数目

所以 \(P(A|B)=\frac{P(AB)}{P(B)}\) 得证，反之就是 \(P(B|A)=\frac{P(AB)}{P(A)}\)

根据根据贝叶斯公式可以直接推出下面两个等式：

• 概率乘法公式: 在概率空间 \((\Omega,\mathcal{F},P )\) ，若 \(P(A)>0\)，则对于任意事件都有 \(P(AB)=P(A)P(B|A)\)。

• 全概率公式: 在概率空间 \((\Omega,\mathcal{F},P )\) ，\(A_1,A_2,\dots,A_n\) 满足：

  • 不重复，\(A_i\cap A_j(i\neq j)\)
  • 不漏（占满整个概率空间），\(B_1 \cup B_2 \cup \dots\cup B_n=\Omega\)

  则任意事件B​，\(P(B)=\sum_{i=1}^{n}P(A_i)P(B|A_i)\)

事件的独立性

定义

若同一概率空间中的事件 \(A,B\) 满足：

\[P(AB)=P(A)P(B) \]

则称 \(A,B\) 独立，多个事件同理。