李超树详解
P4097 【模板】李超线段树
前置知识
大体思路
李超线段树利用线段树思想,
可以支持维护支持区间插入线段,与单点查询最值。
在线段树中,每个节点存放线段的下标,同时,存的这一条线段在该区间内大部分处于比其他线段更高的位置
具体思路
-
变量
int n,cnt; /* cnt:目前线段数 */ struct node { long double k,b; /* k:斜率 b:y轴截距 */ }a[D];//每个线段y轴的斜率、截距 int t[N<<4];//线段树 -
查询
inline int Max(int p,int q,int x) { if(f(p,x)!=f(q,x)) { if(f(p,x)>f(q,x)) { return p; } return q; } return min(p,q); } inline int query(int k,int l,int r,int x)//x:横坐标,k:线段树中的节点下标 { if(l==r)return t[k]; int mid=(l+r)>>1; if(x<=mid)return Max(t[k],query(k<<1,l,mid,x),x); else return Max(t[k],query(k<<1|1,mid+1,r,x),x); /* if,else作用: 求最大的纵坐标 */ } -
修改
下图中橙线指新的一条线,红线指目前在线段树中的线。
设 为橙线, 为红线,
为橙线斜率, 为红线斜率,
为当前线段树区间左端点, 为当前线段树区间右端点,
为前线段树区间中点。
-
-
在 处, 比 高。
在左子树中 仍可能比 高,
这时,我们更新 为这个区间最高的直线,
将 下传至左子树。
-
在 处, 比 低。
在右子树中 仍可能比 高,
这时,我们仍用 作为这个区间最高的直线,
将 下传至右子树。
-
-
-
在 处, 比 高。
在右子树中 仍可能 比 高,
这时,我们更新 为这个区间最高的直线,
将 下传至右子树。
-
在 处, 比 低。
在左子树中 仍可能 比 高,
这时,我们仍用 作为这个区间最高的直线,
将 下传至左子树。
-
-
在区间内,起点高,终点高。
这样的话, 就没用了,将 取代 。
-
在区间内,起点高,终点高。
这样的话, 就没用了,保留 。
加一条线段时的代码如下:
inline long double f(int w,int x){return {a[w].k*x+a[w].b};} inline void modify(int k,int l,int r,int x,int y,int w) { int mid=(l+r)>>1; if(x<=l&&r<=y)//将整个区间包含 {//下面就是上述分类讨论 if(f(w,l)>f(t[k],l)&&f(w,r)>f(t[k],r))//起点终点都高 ,更改 { t[k]=w; return; } if(f(w,l)<=f(t[k],l)&&f(w,r)<=f(t[k],r))//起点终点都矮 ,直接return { return; } if(a[w].k>a[t[k]].k) { if(f(w,mid)>f(t[k],mid)) { modify(k<<1,l,mid,x,y,t[k]); t[k]=w; } else { modify(k<<1|1,mid+1,r,x,y,w); } } else { if(f(w,mid)>f(t[k],mid)) { modify(k<<1|1,mid+1,r,x,y,t[k]); t[k]=w; } else { modify(k<<1,l,mid,x,y,w); } } return; } if(x<=mid)modify(k<<1,l,mid,x,y,w); if(mid<y) modify(k<<1|1,mid+1,r,x,y,w); } -
总代码(含注释):
#include <bits/stdc++.h>
using namespace std;
const int mod = 39989;
const int Mod = 1000000000;
const int D=1e5+5;
const int N=4e5+5;
int n,cnt;
struct node
{
long double k,b;
}a[D];
int t[N<<4];
inline node get(long double x0,long double y0,long double x1,long double y1)
{//获取k,b
if(x0==x1)return (node){0,max(y0,y1)};
long double k=(y1-y0)/(x1-x0),b=y1-k*x1;
return (node){k,b};
}
inline long double f(int w,int x){return {a[w].k*x+a[w].b};}//获取y坐标
inline void modify(int k,int l,int r,int x,int y,int w)
{
if(l==r)//当区间为一个点时,很好分辨哪个高,哪个低
{
if(f(w,l)>f(t[k],l))
{
t[k]=w;
}
return;
}
int mid=(l+r)>>1;
if(x<=l&&r<=y)//将整个区间包含
{//下面就是上述分类讨论
if(f(w,l)>f(t[k],l)&&f(w,r)>f(t[k],r))//起点终点都高 ,更改
{
t[k]=w;
return;
}
if(f(w,l)<=f(t[k],l)&&f(w,r)<=f(t[k],r))//起点终点都矮 ,直接return
{
return;
}
if(a[w].k>a[t[k]].k)
{
if(f(w,mid)>f(t[k],mid))
{
modify(k<<1,l,mid,x,y,t[k]);
t[k]=w;
}
else
{
modify(k<<1|1,mid+1,r,x,y,w);
}
}
else
{
if(f(w,mid)>f(t[k],mid))
{
modify(k<<1|1,mid+1,r,x,y,t[k]);
t[k]=w;
}
else
{
modify(k<<1,l,mid,x,y,w);
}
}
return;
}
if(x<=mid)modify(k<<1,l,mid,x,y,w);
if(mid<y) modify(k<<1|1,mid+1,r,x,y,w);
}
inline int Max(int p,int q,int x)
{
if(f(p,x)!=f(q,x))
{
if(f(p,x)>f(q,x))
{
return p;
}
return q;
}
return min(p,q);
}
inline int query(int k,int l,int r,int x)
{
if(l==r)return t[k];
int mid=(l+r)>>1;
if(x<=mid)return Max(t[k],query(k<<1,l,mid,x),x);
else return Max(t[k],query(k<<1|1,mid+1,r,x),x);
}
int main()
{
scanf("%d",&n);
int last=0;
for(int i=1,op,x0,x1,y0,y1,k;i<=n;i++)
{
scanf("%d",&op);
if(op==0)
{
scanf("%d",&k);
k=(k+last-1+mod)%mod+1;
last=query(1,1,mod,k);
cout<<last<<'\n';
}
else
{
scanf("%d%d%d%d",&x0,&y0,&x1,&y1);
x0=(x0+last-1+mod)%mod+1;
x1=(x1+last-1+mod)%mod+1;
y0=(y0+last-1+Mod)%Mod+1;
y1=(y1+last-1+Mod)%Mod+1;
if(x0>x1)
{
swap(x0,x1);
swap(y0,y1);
}
a[++cnt]=get(x0,y0,x1,y1);
modify(1,1,mod,x0,x1,cnt);
}
}
return 0;
}
关于Subtask #0 #5
输入:
3
1 8 7 3 9
1 10 9 4 3
0 8
输出:
1
由于double的精度原因,要开 long double !!!
一些可能的疑问:
-
如果两条线的交点恰好在线段树中一个区间的中点怎么办?
其实,这里的线段树主要是使查询时, 找到最大值;修改时, 修改罢了,随便一个下传都可以,因为查询的横坐标总会经过你要的正确答案的。
个人认为比较详细,望通过!!!
其他习题
洛谷 P2497
这是算 的推到过程(推出来 )。。。
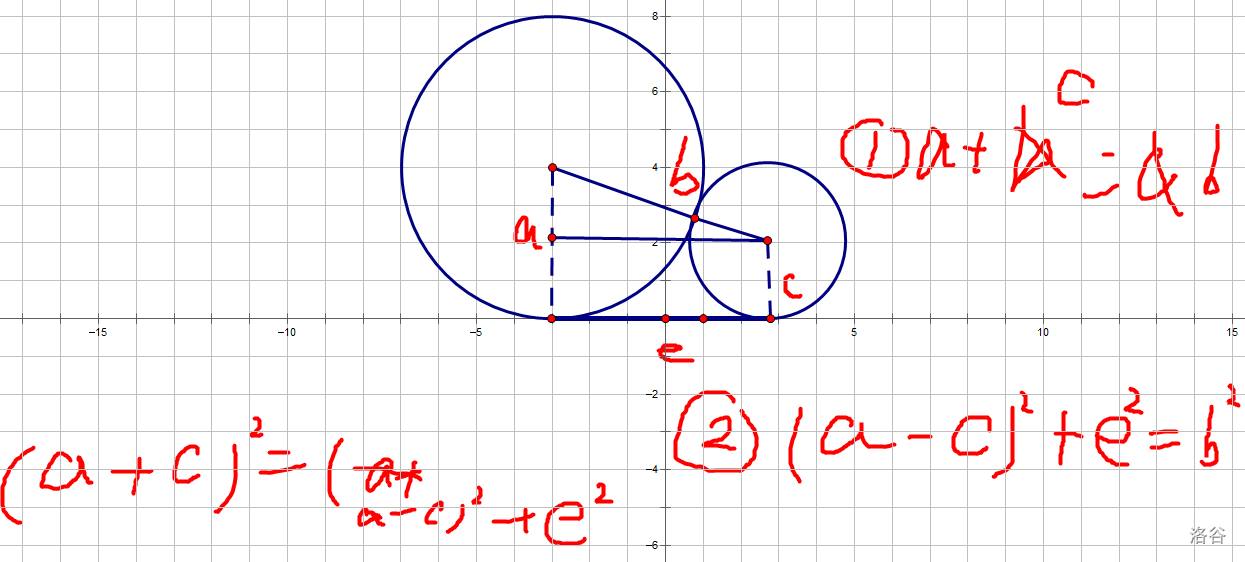
这是 dp 转移方程( 表示 轴上的 点选时的代价)。。。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析