用 python 解 NOIP 竞赛题

以下为2017年全国 NOIP 提高组复赛的第1题：

 

 

怎么样，读完题是不是感觉特别懵。—— 我是谁，我在哪里？

接下来我们来慢慢解析这道让人摸不着头脑的竞赛题。

 

一、首先翻译一下题的意思：

• 假设，现在人民币只有两个币种，面值你定
• 对面值数字的要求是这两个数字不能有公约数（除1这个公约数外）
     例如：2和5
• 问用这两个面值的钱，不能凑齐的最大的价钱是多少
• 当然，前提是你有任意多的钱

是不是稍微要清晰一些了呢。

 

二、那我们接下来用python写一个程序来完成这道题：

整个过程分两步：

第一步：借助 python 找规律划范围

 

# 先找出能凑出来的金额
def myFunc(a, b):  # 输入a,b 两个互素的面值
    c = 1  # 从1开始找出能凑出的金额
    while True:  # 不断循环，电脑配置低的，请远离，前方危险
        for i in range(c):
            an01 = a * i
            for j in range(c):
                an02 = b * j
                if an01 + an02 == c:  # 一旦找到能凑出当前金额c的i和j，打印出来
                    # print(c, "=", a, '*', i, '+', b, '*', j)
                    print(c,end='  ')
        c += 1  # 金额不断上涨，上不封顶


if __name__ == "__main__":
    myFunc(3, 5)

结果为：

 

 

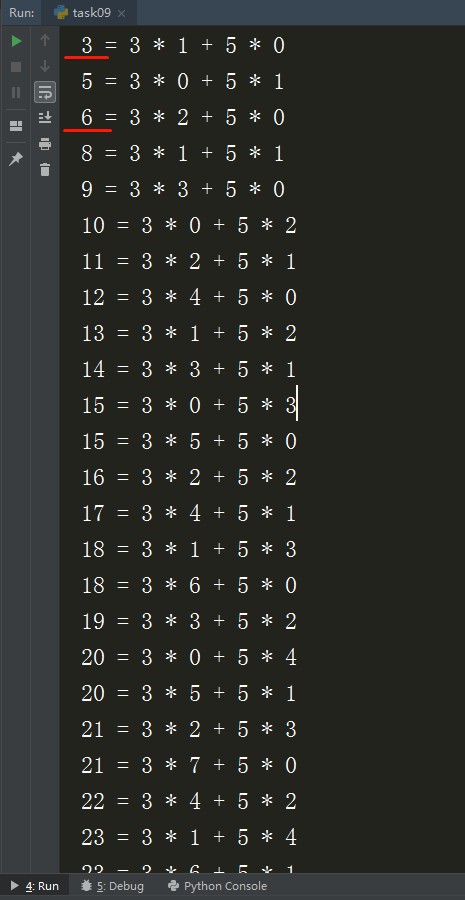
如果将面值设置为 7,5 呢

结果：

 

 

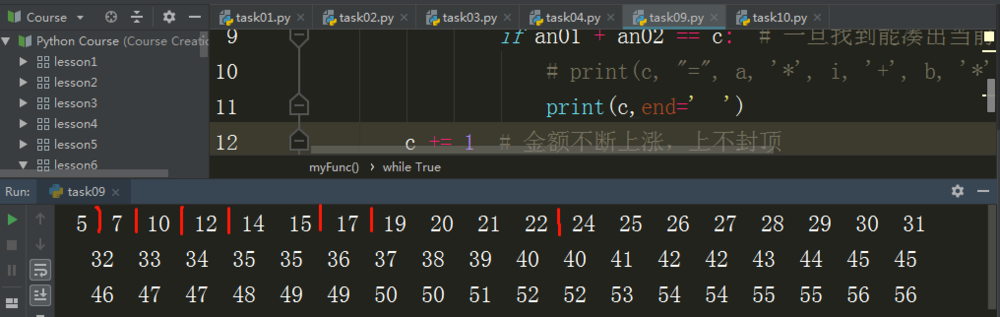
再如果换成 7,9

结果：

 

综上:

•  我们可以发现，不可组合的面值均集中在靠前的位置，但有多靠前，具体又在哪个位置呢？
•  我们姑且假定这个数字就在 两数的乘积 之内，而且事实也是这样的。大家可以多试几对数字，检验一下。

 

 

第二步：范围找到后，我们再来考虑用 python 找出范围内的不可组合的金额值：

  备注：上面的程序是一个死循环，需要手动结束程序，建议不懂操作的小伙伴谨慎运行（嘿嘿，你是不是已经入坑啦！）。但下面这个程序就不一样了，小伙伴们尽管去运行吧。

 

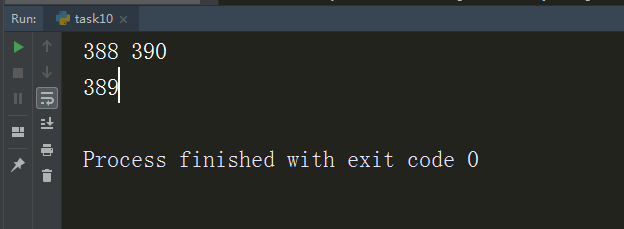
# 找出两数乘积范围内的可组合数据
def myFunc(a, b):
    c = a * b
    my_list = []  # 创建存放所有组合出来的金额值

    # 找寻过程 -- 不断对比
    for i in range(0, c):
        an01 = a * i
        for j in range(c):
            an02 = b * j
            if an01 + an02 <= c:  # 只找在乘积范围内的组合，节省运算次数
                my_list.append(an01 + an02)  # 将符合的金额添加进目标列表
    return list(set(sorted(my_list)))  # 返回经过去重和排序的目标列表


# 找到最大的那个不能组合的金额
def getMax(a, b):
    my_list = myFunc(a, b)  # 调用找可拼凑数据函数得到目标列表
    my_list.sort(reverse=True)  # 将目标列表反序排列

    # 判断目标列表是否连续，并输出断点数中的最大值
    y = my_list[0] + 1  # 创建对比参数
    for x in my_list:
        if x + 1 != y:
            print(x, y)
            break
        y = x
    return y - 1  # 返回最大断点值


if __name__ == "__main__":
    print(getMax(16, 27))

 

 结果为：

 

 

三、总结

不知道大家有没有发现一个问题，这个最大不可组合数据似乎有一定的规律，规律为：

 

　　c = a * b - a - b

 

 

( 其中的a 和 b 为你输入的两个互为素数的币种面值，c为它们不能组合的金额 )
大家可以多试几组数据，验证一下。

 

而且我要悄悄告诉你的就是，这个公式可是一个牛哄哄的定理，名字叫：赛瓦维斯特定理

　　赛瓦维斯特定理:

　　　　已知a,b为大于1的正整数，(a,b)=1,则使不定方程 ax+by=c 无负整数解的最大整数c=ab−a−b   

　　　　其中的 (a,b) 表示a和b的最大公约数

 

 

 

 

 

怎么样，通过两个程序，我们就很容易的解决了这个看起来不那么友好的竞赛题。
此时，是不是觉得 python 很酷呢！

笔者会不定时的更新一些跟python相关又和数学相关的一些有趣的程序，喜欢就关注我吧。

 

特别警示：本文为作者原创作品，禁止不经过本人同意就将其转载用于商业用途，否则将予以追究。
处于学习分享转载请附上出处链接，谢谢！