从DDPM到DDIM (二) 前向过程与反向过程的概率分布
本文是从DDPM到DDIM系列的第二篇,没看过第一篇的同志可以去阅读第一篇。我们这篇文章的小节序号和公式序号都沿用上一篇文章。
我们这里先简单回顾一下上一篇文章中一些重要的点。
扩散模型的结构和特点。下图展示了DDPM原文中的马尔可夫模型。
![img]()
其中\(\mathbf{x}_T\)代表纯高斯噪声,\(\mathbf{x}_t, 0 < t < T\) 代表中间的隐变量, \(\mathbf{x}_0\) 代表生成的图像。从 \(\mathbf{x}_0\) 逐步加噪到 \(\mathbf{x}_T\) 的过程是不需要神经网络参数的,简单地讲高斯噪声和图像或者隐变量进行线性组合即可,单步加噪过程用\(q(\mathbf{x}_t | \mathbf{x}_{t-1})\)来表示。但是去噪的过程,我们是不知道的,这里的单步去噪过程,我们用 \(p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})\) 来表示。之所以这里增加一个 \(\theta\) 下标,是因为 \(p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})\) 是用神经网络来逼近的转移概率, \(\theta\) 代表神经网络参数。
联合概率表示 扩散模型的联合概率和前向条件联合概率为:
\[\begin{aligned}
{p\left(\mathbf{x}_{0:T}\right) = p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1}|\mathbf{x}_{t}\right)}
\end{aligned} \tag{1}
\]
\[\begin{aligned}
{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right) = \prod_{t=1}^T q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)} \\
\end{aligned} \tag{2}
\]
证据下界 我们原本要对生成的图像分布进行极大似然估计,但直接估计无法计算。于是我们改为最大化证据下界,然后对证据下界进行化简,化简之后的结果如下:
\[\begin{aligned}
\log p\left(\mathbf{x}_0\right) &\geq \mathcal{L} \\
&= \mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \frac{p\left(\mathbf{x}_{T}\right) p_{\theta}\left(\mathbf{x}_{0}|\mathbf{x}_{1}\right) \prod_{t=1}^{T-1} \textcolor{blue}{p_{\theta}\left(\mathbf{x}_{t}|\mathbf{x}_{t+1}\right)}}{\prod_{t=1}^T \textcolor{blue}{q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)}}\right] \\
&= \mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \frac{p\left(\mathbf{x}_{T}\right) p_{\theta}\left(\mathbf{x}_{0}|\mathbf{x}_{1}\right) \prod_{t=1}^{T-1} {p_{\theta}\left(\mathbf{x}_{t}|\mathbf{x}_{t+1}\right)}}{q\left(\mathbf{x}_{T} | \mathbf{x}_{T-1}\right) \prod_{t=1}^{T-1} {q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)}}\right] \\
&= \mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \frac{p\left(\mathbf{x}_{T}\right) p_{\theta}\left(\mathbf{x}_{0}|\mathbf{x}_{1}\right)}{q\left(\mathbf{x}_{T} | \mathbf{x}_{T-1}\right) }\right] + \mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \prod_{t=1}^{T-1} \frac{p_{\theta}\left(\mathbf{x}_{t}|\mathbf{x}_{t+1}\right)}{q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)} \right]\\
&= \textcolor{skyblue}{\mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log p_{\theta}\left(\mathbf{x}_{0}|\mathbf{x}_{1}\right) \right]} + \textcolor{darkred}{\mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \frac{p\left(\mathbf{x}_{T}\right)}{q\left(\mathbf{x}_{T} | \mathbf{x}_{T-1}\right)} \right]} + \textcolor{darkgreen}{\sum_{t=1}^{T-1} \mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log \frac{p_{\theta}\left(\mathbf{x}_{t}|\mathbf{x}_{t+1}\right)}{q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)} \right]} \\
&= \textcolor{skyblue}{\mathbb{E}_{q\left(\mathbf{x}_{1:T} | \mathbf{x}_{0}\right)} \left[ \log p_{\theta}\left(\mathbf{x}_{0}|\mathbf{x}_{1}\right) \right]} - \textcolor{darkred}{\mathbb{E}_{q\left(\mathbf{x}_{T-1} | \mathbf{x}_{0}\right)} \left[ \mathbb{D}_{\text{KL}}\left(q\left(\mathbf{x}_{T} | \mathbf{x}_{T-1}\right) || p\left(\mathbf{x}_{T}\right)\right) \right]} \\
&- \textcolor{darkgreen}{\sum_{t=1}^{T-1} \mathbb{E}_{q\left(\mathbf{x}_{t-1}, \mathbf{x}_{t+1} | \mathbf{x}_{0}\right)} \left[ \mathbb{D}_{\text{KL}}\left(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right) || p_{\theta}\left(\mathbf{x}_{t}|\mathbf{x}_{t+1}\right)\right) \right]} \\
\end{aligned} \tag{3}
\]
3、优化证据下界
3.1、利用贝叶斯公式和马尔可夫性进行条件概率改造
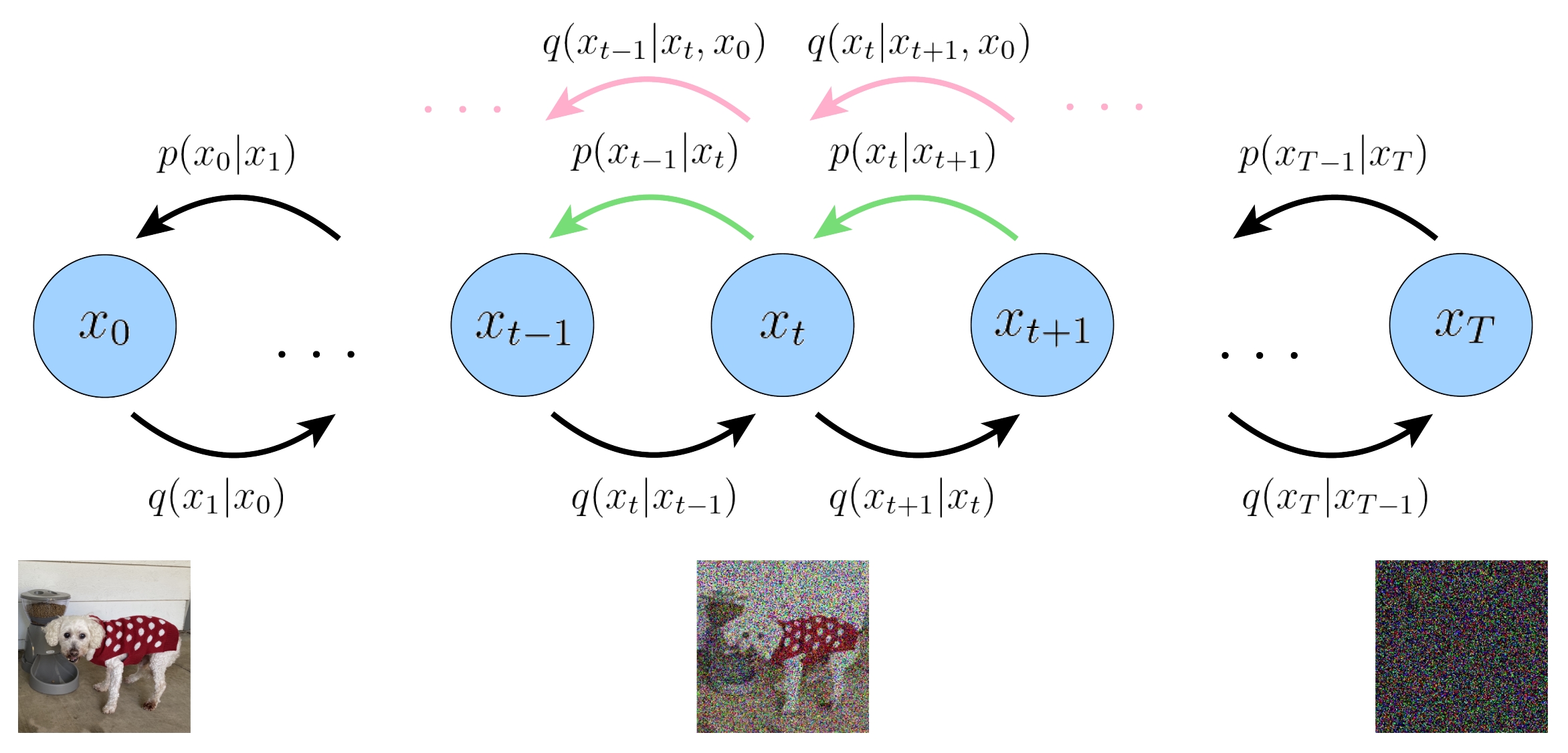
上一节我们讨论到。直接优化证据下界会导致优化的单步转移概率在时序上错一位的问题。这个问题是如何发生的呢?一开始(3)式的分子分母对应的单步转移概率是 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 和 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\)。这里二者描述的是两个不同的随机变量的分布,\(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 描述的是 \(\mathbf{x}_{t-1}\) 这个随机变量的分布,而 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\) 描述的是随机变量 \(\mathbf{x}_{t}\) 的分布。针对两个不同随机变量分布显然是没有可比性的。
我们之前采用的方法是错位比较,即 \(p_{\theta}\left(\mathbf{x}_{t} | \mathbf{x}_{t+1}\right)\) 和 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\) 进行比较。这样做有两个缺点,第一是时序上错位,第二是传递方向也是不相同的,所以我们本节采用另一种思路来解决这个问题。
首先我们联想到贝叶斯公式,这个数学工具可以让随机变量与条件随机变量互换。那么我们要改造 \(p\),还是改造 \(q\) 呢?当然是改造 \(q\),因为 \(q\) 是我们已知的分布,\(p\) 是我们要求的分布,你如果改造 \(p\) 的话就偏离了我们的主要方向了。因此要改造 \(q\)。具体如下:
\[\begin{aligned}
q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right) = \frac{\textcolor{red}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)} q\left(\mathbf{x}_{t}\right)}{q\left(\mathbf{x}_{t-1}\right)}
\end{aligned} \tag{4}
\]
\(\textcolor{red}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)}\) 就是我们希望优化的目标,因为它和 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 的形式简直一模一样!而且二者的传递方向也一样,简直完美。
但是,很可惜,我们无法通过 (4) 式来求出 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)}\),因为我们只知道 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\)。而 \(q\left(\mathbf{x}_{t}\right)\) 和 \(q\left(\mathbf{x}_{t-1}\right)\) 我们都不知道啊!
办法总比困难多,别忘了,贝叶斯公式对各种的条件分布都成立,但我们这里还有一个额外条件,那就是马尔可夫性啊!所以 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right) = q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right)\)。利用这个思路,我们对 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right)\) 进行贝叶斯改造,有:
\[\begin{aligned}
q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right) = \frac{\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)}
\end{aligned} \tag{5}
\]
这样,我们用 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\) 来拟合神经网络 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\),进而对证据下界进行化简。有同学可能会问 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)\) 的物理意义。笔者认为这只是一个数学上的中间变量,并无物理意义。如果硬要解释的话,或许就是在给定最终生成结果 \(\mathbf{x}_{0}\) 的条件下,生成过程的单步转移概率。\(\mathbf{x}_{0}\) 就像有监督学习中的标签,指导着生成的方向,因此用 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\) 来拟合神经网络 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 相当于指导神经网络向正确的方向生成。
现在我们分析一下能够利用(5)式来求出 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\)。(5)式等式左边我们是知道的,如果等式右边的 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)\) 和 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)\) 知道的话,那么我们就可以计算 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\) 了。
那么等式右边的 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)\) 和 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)\) 可以求吗?答案是,当然可以!这两个分布我们称其为扩散过程的多步转移概率,而要求解之,必须知道单步转移概率 \(q(\mathbf{x}_{t} | \mathbf{x}_{t-1})\)。下面我们就来求扩散过程的单步转移概率和多步转移概率。
![img]()
3.2、扩散过程的单步转移概率 \(q(\mathbf{x}_{t} | \mathbf{x}_{t-1})\)
先回顾一下DDPM的扩散过程,扩散过程是对图片 \(\mathbf{x}_0\) 不断加高斯噪声的过程。这里并不是简单的直接相加,而是设定了权重,原始图像和高斯噪声加权相加。这当然也包含了简单相加的情况,而我们采用加权相加,其实是有这样的考虑:
- 我们希望噪声添加之后,新的图像和旧的图像查别不会太大。否则在恢复图像的时候就有更大的困难。这就要求加权加噪的时候,原始图像的权重要很大,噪声的权重很小。从理论的角度来讲,只有当噪声方差很小的时候,扩散过程 \(q(\mathbf{x}_{t} | \mathbf{x}_{t-1})\) 和采样过程 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t})\) 才服从一样的分布,比如都是高斯分布。
- 由于我们加噪的终点是要把图像加噪成纯高斯噪声,而每一步的高斯噪声都很轻微,这就必然要求要加噪很多步骤。水滴石穿嘛。DDPM设定的是1000步。DDIM的扩散阶段与DDPM是相同的,但DDIM在采样过程只需要50步,这并不是因为马尔可夫链长度只有50,而是DDIM在采样的时候没有遵从马尔可夫性,选择了“跳步”。比如从1000步,直接跳到980步,然后跳到960步。关于DDIM的具体原理我们之后再聊。
- 添加噪声必须保证能量不变。这是显然的道理,图像像素值只能是0-255的整数。我们必须保证归一化尺度不变。
下面具体来看加噪过程。令 \(\beta_{t}\) 代表第 \(t\) 步添加的噪声的方差,噪声的均值为0。假设 \(\sqrt{\gamma_{t}}\) 代表第 \(t-1\) 步的随机变量的权重。那么添加噪声的过程可以用下式来描述:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\gamma_{t}} \mathbf{x}_{t-1} + \sqrt{\beta_{t}} \epsilon_{t-1} \\
\end{aligned} \\
\]
其中 $\epsilon_{i} $ 代表服从标准高斯分布的随机变量,即 \(\epsilon_{i} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)。
图像不断添加噪声,肯定有一个条件,那就是图像的能量必须保持不变。而图像的能量可以用下式来计算:
\[\begin{aligned}
\mathbb{E} \left[\Vert \mathbf{x}_{t} \Vert_2^2\right] &= \mathbb{E} \left[\Vert \sqrt{\gamma_{t}} \mathbf{x}_{t-1} \Vert_2^2\right] + 2 \mathbb{E} \left[\langle \sqrt{\gamma_{t}} \mathbf{x}_{t-1}, \sqrt{\beta_{t}} \epsilon_{t-1}\rangle\right] + \mathbb{E} \left[\Vert \sqrt{\beta_{t}} \epsilon_{t-1} \Vert_2^2\right] \\
&= \gamma_{t} \mathbb{E} \left[\Vert \mathbf{x}_{t-1} \Vert_2^2\right] + 0 + \beta_{t} \quad\quad 噪声与\mathbf{x}_{t-1}不相关,标准高斯噪声能量是1\\
&= \gamma_{t} \mathbb{E} \left[\Vert \mathbf{x}_{t-1} \Vert_2^2\right] + \beta_{t}\\
\end{aligned} \\
\]
我们在对原始图像 \(\mathbf{x}_0\) 进行预处理的时候。必须有归一化的操作 (归一化是数据处理的基本操作),因此 \(\mathbf{x}_0\) 的能量为 \(1\),每次加噪声保持能量不变,所以对于任意时刻,\(\mathbf{x}_{t}\) 的能量 \(\mathbb{E} \left[\Vert \mathbf{x}_{t} \Vert_2^2\right] = 1\),所以:
\[\begin{aligned}
\gamma_{t} \mathbb{E} \left[\Vert \mathbf{x}_{t-1} \Vert_2^2\right] + \beta_{t} &= \mathbb{E} \left[\Vert \mathbf{x}_{t-1} \Vert_2^2\right]\\
\gamma_{t} + \beta_{t} &= 1\\
\gamma_{t} &= 1 - \beta_{t}\\
\end{aligned} \\
\]
于是扩散过程(加噪过程)的递推公式为:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{1 - \beta_{t}} \mathbf{x}_{t-1} + \sqrt{\beta_{t}} \epsilon_{t-1} \\
\end{aligned}
\]
可以看到,在给定条件 \(\mathbf{x}_{t-1}\) 下,\(\mathbf{x}_{t}\) 的条件概率服从均值为 \(\sqrt{1 - \beta_t} \mathbf{x}_{t-1}\),方差为 \(\beta_t\) 的高斯分布:
\[\begin{aligned}
q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) \\
&= \mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I})
\end{aligned} \\
\]
为了之后便于推导,我们令 \(\alpha_t = 1 - \beta_t\),于是有:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\alpha_{t}} \mathbf{x}_{t-1} + \sqrt{1 - \alpha_{t}} \epsilon_{t-1} \\
q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I})
\end{aligned} \tag{6}
\]
到这里,我们就得出了扩散过程的单步转移概率 \(q(\mathbf{x}_{t} | \mathbf{x}_{t-1})\)。
3.3、扩散过程的多步转移概率 \(q(\mathbf{x}_{t} | \mathbf{x}_{0})\)
事实上我们可以从最开始 \(\mathbf{x}_{0}\) 的直接一步添加噪声到 \(\mathbf{x}_{t}\)。这个过程我们用多步转移概率 \(q(\mathbf{x}_{t} | \mathbf{x}_{0})\) 来描述。这个条件分布依然是高斯分布。下面我们就来证明这一点。
我们从(6)的递推形式入手,一步步得出 \(\mathbf{x}_{t}\) 与 \(\mathbf{x}_{0}\) 的关系:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\alpha_t} \mathbf{x}_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \\
&= \sqrt{\alpha_t} (\sqrt{\alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \epsilon_{t-1}) + \sqrt{1 - \alpha_t} \epsilon_{t-2} \\
&= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{\alpha_t (1 - \alpha_{t-1})} \epsilon_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-2} \\
\end{aligned} \\
\]
根据高斯分布的相加性质:假设随机变量 \(X\) 与 \(Y\) 相互独立,且服从高斯分布,其概率密度函数分别为 \(f_X(x)\) 和 \(f_Y(y)\),则 \(Z = X + Y\) 也服从高斯分布。其均值为两个随机变量均值之和,方差为两个随机变量方差之和。于是:
\[\begin{aligned}
\sqrt{\alpha_t (1 - \alpha_{t-1})} \epsilon_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-2} &= \sqrt{\alpha_t (1 - \alpha_{t-1}) + 1 - \alpha_t} \overline{\epsilon}_{t-2} \\
&= \sqrt{1 - \alpha_t \alpha_{t-1}} \overline{\epsilon}_{t-2} \\
\end{aligned} \\
\]
其中 \(\overline{\epsilon}_{t-2} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\),于是有:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \overline{\epsilon}_{t-2} \\
\end{aligned} \tag{7}
\]
到这里发现规律了。(7)式相比于(6)式,右边第一项的系数的根号下多乘了一个 \(\alpha_{t-1}\),第二项的系数也有类似的规律。于是令 \(\overline{\alpha}_t := \prod_{s=1}^t \alpha_s\),猜想有以下规律:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\
\end{aligned} \\
\]
证明: 第一步,证明 \(t = 1\) 时刻是否成立。
\[\begin{aligned}
\mathbf{x}_{1} &= \sqrt{\alpha_1} \mathbf{x}_{0} + \sqrt{1 - \alpha_1} \epsilon_{0} \\
&= \sqrt{\overline{\alpha}_1} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_1} \epsilon_{0} \\
\end{aligned} \\
\]
结论:成立。
第二步,假设 \(t = n\) 成立,证明 \(t = n + 1\) 时刻成立。根据假设,我们有:
\[\begin{aligned}
\mathbf{x}_{n} &= \sqrt{\overline{\alpha}_n} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_n} \epsilon \\
\end{aligned} \\
\]
于是 \(\mathbf{x}_{n+1}\) 为:
\[\begin{aligned}
\mathbf{x}_{n+1} &= \sqrt{\alpha_{n+1}} \mathbf{x}_{n} + \sqrt{1 - \alpha_{n+1}} \epsilon_{n} \\
&= \sqrt{\alpha_{n+1}} (\sqrt{\overline{\alpha}_n} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_n} \epsilon) + \sqrt{1 - \alpha_{n+1}} \epsilon_{n} \\
&= \sqrt{\alpha_{n+1} \overline{\alpha}_n} \mathbf{x}_{0} + \sqrt{\alpha_{n+1} (1 - \overline{\alpha}_n)} \epsilon + \sqrt{1 - \alpha_{n+1}} \epsilon_{n} \\
&= \sqrt{\alpha_{n+1} \overline{\alpha}_n} \mathbf{x}_{0} + \sqrt{1 - \alpha_{n+1}\overline{\alpha}_n} \overline{\epsilon} \quad (高斯分布的相加性质) \\
&= \sqrt{\overline{\alpha}_{n+1}} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_{n+1}} \overline{\epsilon} \\
\end{aligned} \\
\]
结论:\(t = n + 1\) 时刻成立。
证毕。
到这里,我们就的处理扩散过程的多步转移概率:
\[\begin{aligned}
\mathbf{x}_{t} &= \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} + \sqrt{1 - \overline{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\
q(\mathbf{x}_{t} | \mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t}; \sqrt{\overline{\alpha}_t} \mathbf{x}_{0}, (1 - \overline{\alpha}_t) \mathbf{I})
\end{aligned} \tag{8}
\]
3.4、计算 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\)
我们目标是计算 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\),以此作为神经网络单步生成的拟合目标。我们已知的是以下的关系:
\[\begin{aligned}
q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right) &= \frac{\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)}\\
q(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I})\\
q(\mathbf{x}_{t} | \mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t}; \sqrt{\overline{\alpha}_t} \mathbf{x}_{0}, (1 - \overline{\alpha}_t) \mathbf{I}) \\
q(\mathbf{x}_{t-1} | \mathbf{x}_{0}) &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0}, (1 - \overline{\alpha}_{t-1}) \mathbf{I}) \\
\end{aligned}
\]
好了,开算!
\[\begin{aligned}
\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} &= \frac{q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right) q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)}\\
&= \frac{\mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I}) \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0}, (1 - \overline{\alpha}_{t-1}) \mathbf{I})}{\mathcal{N}(\mathbf{x}_{t}; \sqrt{\overline{\alpha}_{t}} \mathbf{x}_{0}, (1 - \overline{\alpha}_{t}) \mathbf{I})}\\
\end{aligned} \tag{9}
\]
由于协方差矩阵是对角矩阵,所以我们可以按照标量随机变量来算。由于:
\[\mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I}) = \frac{1}{\sqrt{2 \pi \left(1 - \alpha_t\right)}} \exp \left[-\frac{\left(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{2 \left(1 - \alpha_t\right)}\right]
\]
其他两个高斯分布都类似地写出来,然后硬算肯定能算出来的。教程就展示了硬算的结果。不过我们这里采用中的办法,这里包含一些小技巧,简化我们的计算。
首先我们知道的是在深度学习推导中,系数往往是不重要的,函数形式是最重要的。因此我们可以只看指数项,显然有:
\[\begin{aligned}
\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} &\propto \exp \left[-\frac{\left(\mathbf{x}_{t} - \sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{2 \left(1 - \alpha_t\right)} - \frac{\left(\mathbf{x}_{t-1} - \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0} \right)^2}{2 \left( 1 - \overline{\alpha}_{t-1} \right)} + \frac{\left(\mathbf{x}_t - \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} \right)^2}{2 \left( 1 - \overline{\alpha}_t \right)} \right]\\
\end{aligned}
\]
我们的目标是配方,我们要求的是随机变量 \(\mathbf{x}_{t-1}\) 的条件分布。所以我们试图将 \(\exp\) 中的项配方成
\[-\frac{\left(\mathbf{x}_{t-1} - {\mu}\right)^2}{2 \sigma^2}
\]
这种形式。其中 \(\mu\) 和 \(\sigma\) 是待定系数。我们令:
\[\begin{aligned}
f\left(\mathbf{x}_{t-1}\right) &= -\frac{\left(\mathbf{x}_{t-1} - {\mu}\right)^2}{2 \sigma^2} \\
&= -\frac{\left(\mathbf{x}_{t} - \sqrt{\alpha_t} \mathbf{x}_{t-1}\right)^2}{2 \left(1 - \alpha_t\right)} - \frac{\left(\mathbf{x}_t - \sqrt{\overline{\alpha}_t} \mathbf{x}_{0} \right)^2}{2 \left( 1 - \overline{\alpha}_t \right)} + \frac{\left(\mathbf{x}_{t-1} - \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0} \right)^2}{2 \left( 1 - \overline{\alpha}_{t-1} \right)}
\end{aligned} \tag{10}
\]
计算\(\mu\)
我们令 \(f\left(\mathbf{x}_{t-1}\right)\) 对 \(\mathbf{x}_{t-1}\) 求导,并让其等于零。我们发现其导数的零点就是 \(\mu\)。
\[\begin{aligned}
\frac{d f\left(\mathbf{x}_{t-1}\right)}{d \mathbf{x}_{t-1}} &= -\frac{\mathbf{x}_{t-1} - {\mu}}{\sigma^2} = 0 \\
\mathbf{x}_{t-1} &= \mu
\end{aligned}
\]
下面我们对 (10) 式子下面那一堆公式求导,得:
\[\begin{aligned}
\frac{d f\left(\mathbf{x}_{t-1}\right)}{d \mathbf{x}_{t-1}} &= -\frac{ -\sqrt{\alpha_t} \left(\mathbf{x}_{t} - \sqrt{\alpha_t} \mathbf{x}_{t-1}\right)}{\left(1 - \alpha_t\right)} - \frac{\left(\mathbf{x}_{t-1} - \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0} \right)}{\left( 1 - \overline{\alpha}_{t-1} \right)} \\
&= -\frac{ \left( 1 - \overline{\alpha}_{t-1} \right) \sqrt{\alpha_t} \left(-\mathbf{x}_{t} + \sqrt{\alpha_t} \mathbf{x}_{t-1}\right) + \left(1 - \alpha_t\right) \left(\mathbf{x}_{t-1} - \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0} \right)}{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)} \\
\end{aligned}
\]
根据 \(\overline{\alpha}_{t}\) 的定义,有 \(\overline{\alpha}_{t-1} \alpha_{t} = \overline{\alpha}_{t}\),于是:
\[\begin{aligned}
\frac{d f\left(\mathbf{x}_{t-1}\right)}{d \mathbf{x}_{t-1}} &= -\frac{\left( 1 - \overline{\alpha}_{t} \right) \mathbf{x}_{t-1} - \left( 1 - \overline{\alpha}_{t-1} \right) \sqrt{\alpha_t} \mathbf{x}_{t} - \left(1 - \alpha_t\right) \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0}}{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)} = 0 \\
\end{aligned} \tag{11}
\]
\[\begin{aligned}
\mathbf{x}_{t-1} &= \frac{\left( 1 - \overline{\alpha}_{t-1} \right) \sqrt{\alpha_t} \mathbf{x}_{t}}{\left( 1 - \overline{\alpha}_{t} \right)} + \frac{\left(1 - \alpha_t\right) \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0}}{\left( 1 - \overline{\alpha}_{t} \right)} \\
\end{aligned}
\]
所以我们求出来了 \(\mu\):
\[\begin{aligned}
\mu &= \frac{\left( 1 - \overline{\alpha}_{t-1} \right) \sqrt{\alpha_t}}{\left( 1 - \overline{\alpha}_{t} \right)} \mathbf{x}_{t} + \frac{\left(1 - \alpha_t\right) \sqrt{\overline{\alpha}_{t-1}}}{\left( 1 - \overline{\alpha}_{t} \right)} \mathbf{x}_{0} \\
\end{aligned}
\]
计算\(\sigma^2\)
下面我们求 \(\sigma^2\)。方法类似,我们对 (9)式 求二阶导,我们发现:
\[\begin{aligned}
\frac{d^2 f\left(\mathbf{x}_{t-1}\right)}{d \mathbf{x}_{t-1}^2} &= -\frac{1}{\sigma^2}\\
\end{aligned} \tag{12}
\]
好,继续对 (10) 式的第二行求二阶导。相当于对 (11)式求一阶导:
\[\begin{aligned}
\frac{d^2 f\left(\mathbf{x}_{t-1}\right)}{d \mathbf{x}_{t-1}^2} &= -\frac{ 1 - \overline{\alpha}_{t} }{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)} \\
\end{aligned} \tag{13}
\]
对比 (12) 式和 (13) 式,可以得出:
\[\begin{aligned}
\sigma^2 &= \frac{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)}{ 1 - \overline{\alpha}_{t} } = \frac{\left( 1 - \overline{\alpha}_{t-1} \right)}{ 1 - \overline{\alpha}_{t} } \beta_t\\
\end{aligned}
\]
这是采用求导的方式巧妙计算。这么计算有一个前提,就是你确定 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 是服从高斯分布的,这样才能假设 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 其存在 (15) 式这样的形式。当然,如果从 (9) 式开始一点点化简,也是可以得出 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 是高斯分布的结论。
之前我们只考虑了指数项,为了严谨起见,我们代入高斯分布的前面的系数,来检查一下到底是不是高斯分布。观察 (9) 式:
\[\begin{aligned}
\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} &= \frac{q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}, \mathbf{x}_{0}\right) q\left(\mathbf{x}_{t-1} | \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t} | \mathbf{x}_{0}\right)}\\
&= \frac{\mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) \mathbf{I}) \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\overline{\alpha}_{t-1}} \mathbf{x}_{0}, (1 - \overline{\alpha}_{t-1}) \mathbf{I})}{\mathcal{N}(\mathbf{x}_{t}; \sqrt{\overline{\alpha}_{t}} \mathbf{x}_{0}, (1 - \overline{\alpha}_{t}) \mathbf{I})}\\
&= \frac{\frac{1}{\sqrt{2 \pi \left(1 - \alpha_t\right)}} \frac{1}{\sqrt{2 \pi \left(1 - \overline{\alpha}_{t-1}\right)}}}{\frac{1}{\sqrt{2 \pi \left(1 - \overline{\alpha}_{t}\right)}}} * \exp(\cdot)\\
&= \frac{1}{\sqrt{2 \pi \left(\frac{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)}{ 1 - \overline{\alpha}_{t} }\right)}} * \exp(\cdot)\\
\end{aligned}
\]
同样可以计算出方差,和 (18) 式完全相同。
如果我们推广到多维随机变量,我们得出 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)\) 的表达式,以及均值和方差:
\[\begin{aligned}
\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)} &= \textcolor{blue}{\mathcal{N}(\mathbf{x}_{t-1}; \tilde{\bm{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right) , \tilde{\bm{\Sigma}} \left(t\right))}\\
\textcolor{blue}{\tilde{\bm{\mu}}_{t}} &= \textcolor{blue}{\frac{\left( 1 - \overline{\alpha}_{t-1} \right) \sqrt{\alpha_t}}{\left( 1 - \overline{\alpha}_{t} \right)} \mathbf{x}_{t} + \frac{\left(1 - \alpha_t\right) \sqrt{\overline{\alpha}_{t-1}}}{\left( 1 - \overline{\alpha}_{t} \right)} \mathbf{x}_{0}} \\
\textcolor{blue}{\tilde{\bm{\Sigma}} \left(t\right)} &= \textcolor{blue}{\frac{\left(1 - \alpha_t\right) \left( 1 - \overline{\alpha}_{t-1} \right)}{ 1 - \overline{\alpha}_{t} } \mathbf{I}}\\
\end{aligned}
\]
现在我们来讨论一下 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)\) 、 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 和 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 的区别和联系。
- \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)\),本文一开始讨论过,这里复制一遍。笔者认为这个条件概率只是一个数学上的中间变量,并无物理意义。如果硬要解释的话,或许就是在给定最终生成结果 \(\mathbf{x}_{0}\) 的条件下,生成过程的单步转移概率。\(\mathbf{x}_{0}\) 就像有监督学习中的标签,指导着生成的方向,因此用 \(\textcolor{blue}{q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)}\) 来拟合神经网络 \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 相当于指导神经网络向正确的方向生成。不管 \(\beta_t\),取值如何,只要前向扩散过程服从高斯分布,此条件分布都是服从高斯分布的。
- \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 是真正的采样过程的单步转移概率,但是求解它比较困难,所以我们采用 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0}\right)\) 来代替 \(q\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\)。此条件概率服从高斯分布的前提是\(\beta_t\) 足够小。
- \(p_{\theta}\left(\mathbf{x}_{t-1} | \mathbf{x}_{t}\right)\) 代表的是神经网络拟合的概率,我们希望神经网络能更好地拟合采样过程的单步转移概率。同样,此条件分布服从高斯分布的前提是\(\beta_t\) 足够小。
3.5、利用 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 重新推导证据下界
回顾一下,我们在推导证据下界的时候采用错位比较法,得出计算证据下界要计算 \(p_{\theta}\left(\mathbf{x}_{t} | \mathbf{x}_{t+1}\right)\) 和 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\) 的KL散度,这样存在错位不准确以及方向不准确的问题。后来我们考虑用贝叶斯公式将 \(q\left(\mathbf{x}_{t} | \mathbf{x}_{t-1}\right)\) 改造成 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t})\),但是这个概率我们算不出来。最后我们用 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 来替代 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t})\)。经过一番计算,我们终于计算出了 \(q(\mathbf{x}_{t-1} | \mathbf{x}_{t}, \mathbf{x}_{0})\) 的表达式。下面,我们使用这个式子来重新推导证据下界。这部分我们放到下一篇文章来说。
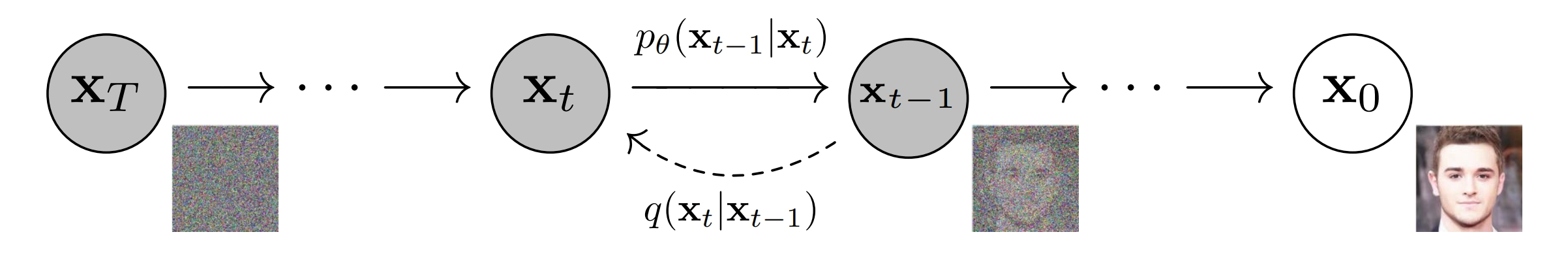



 浙公网安备 33010602011771号
浙公网安备 33010602011771号