算法学习六——NB三人组之堆排序

堆排序

树

树是一种数据结构	比如：目录结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合：
	如果n=0,那这是一颗空树
	如果n>0，那存在1个节点作为数的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树
 

一些概念：

根节点、叶子节点
数的深度(高度)
树的度
孩子节点/父节点
子树

二叉树：

度不超过2的树
每个节点最多有两个孩子节点
两个孩子节点被区分为左孩子节点和右孩子节点

满二叉树：

一个二叉树，如果每一个层的节点数都达到最大值，则这个二叉树就是满二叉树
完全二叉树：
叶节点只能出现在最下层和次下层，并且最下面一层的节点都集中在该层最左边的若干位置的二叉树

二叉树的存储方式(表示方式)

链式存储方式
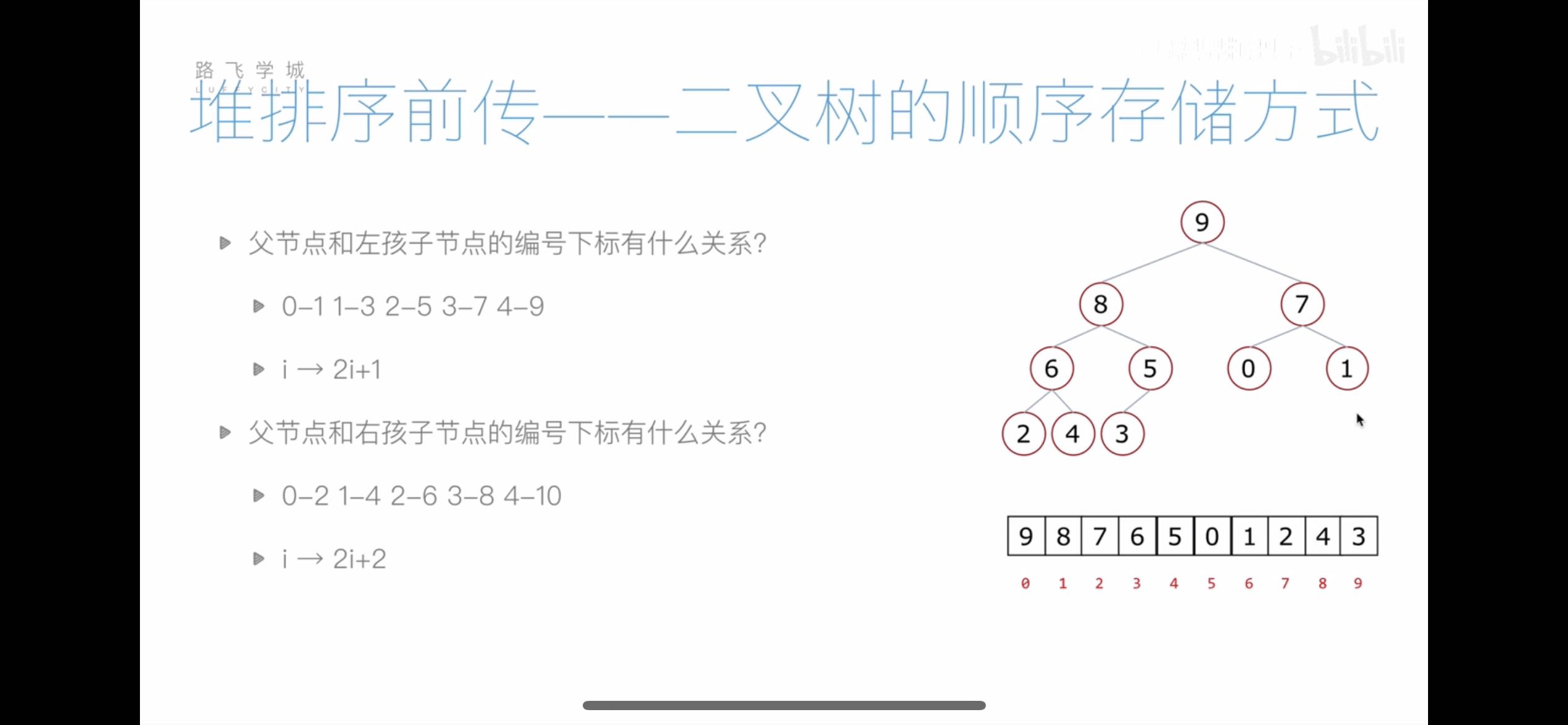
顺序存储方式
 
父节点和左孩子节点的编号小标有什么关系：
	i->2i+1
父节点和右孩子节点的编号下表有什么关系：
	i->2i+2

堆排序——什么是堆

堆：一种特殊的完全二叉树结构
大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大
小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小

堆排序过程

1、建立堆
2、得到堆顶元素，为最大元素
3、去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序
4、堆顶元素为第二大元素
5、重复步骤3，直到堆变空

堆排序——堆的向下调整性质

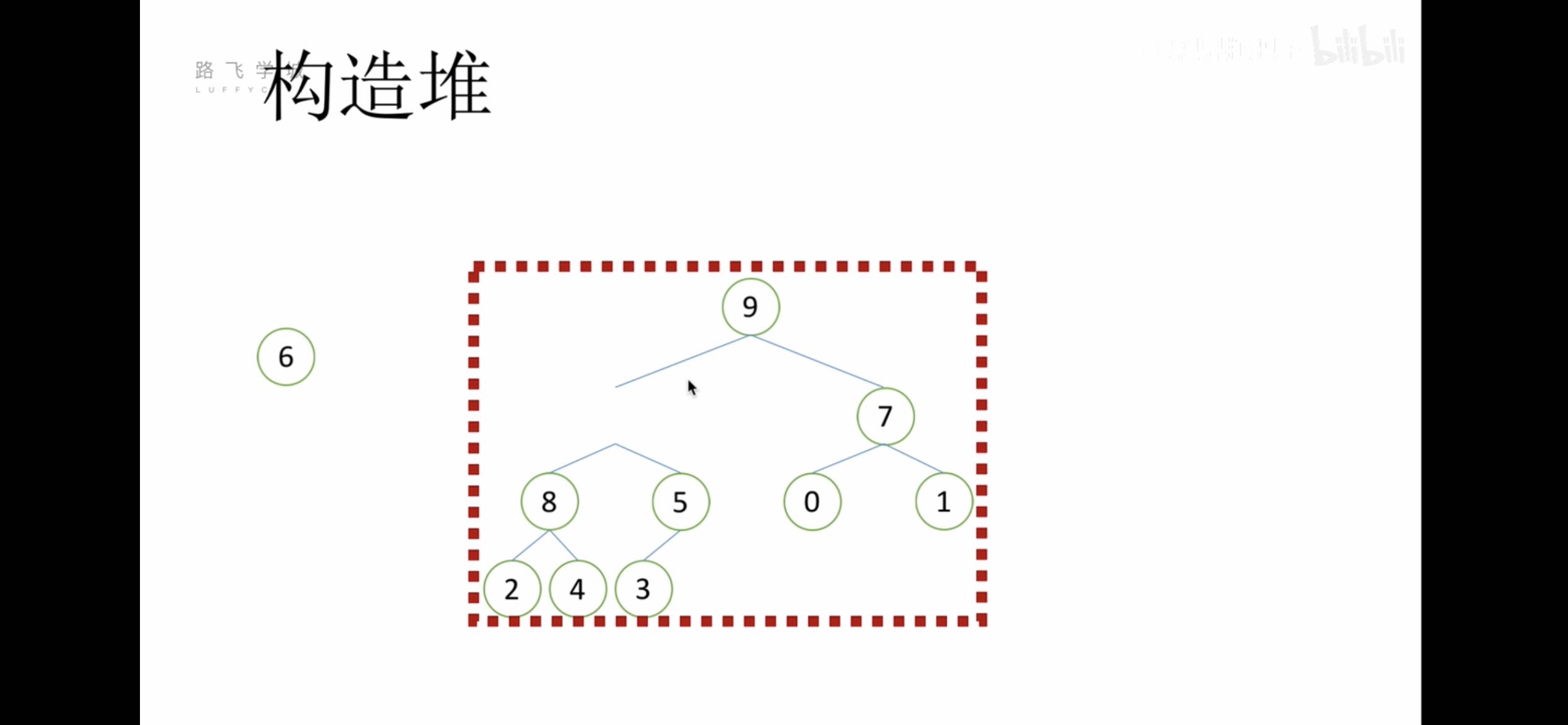
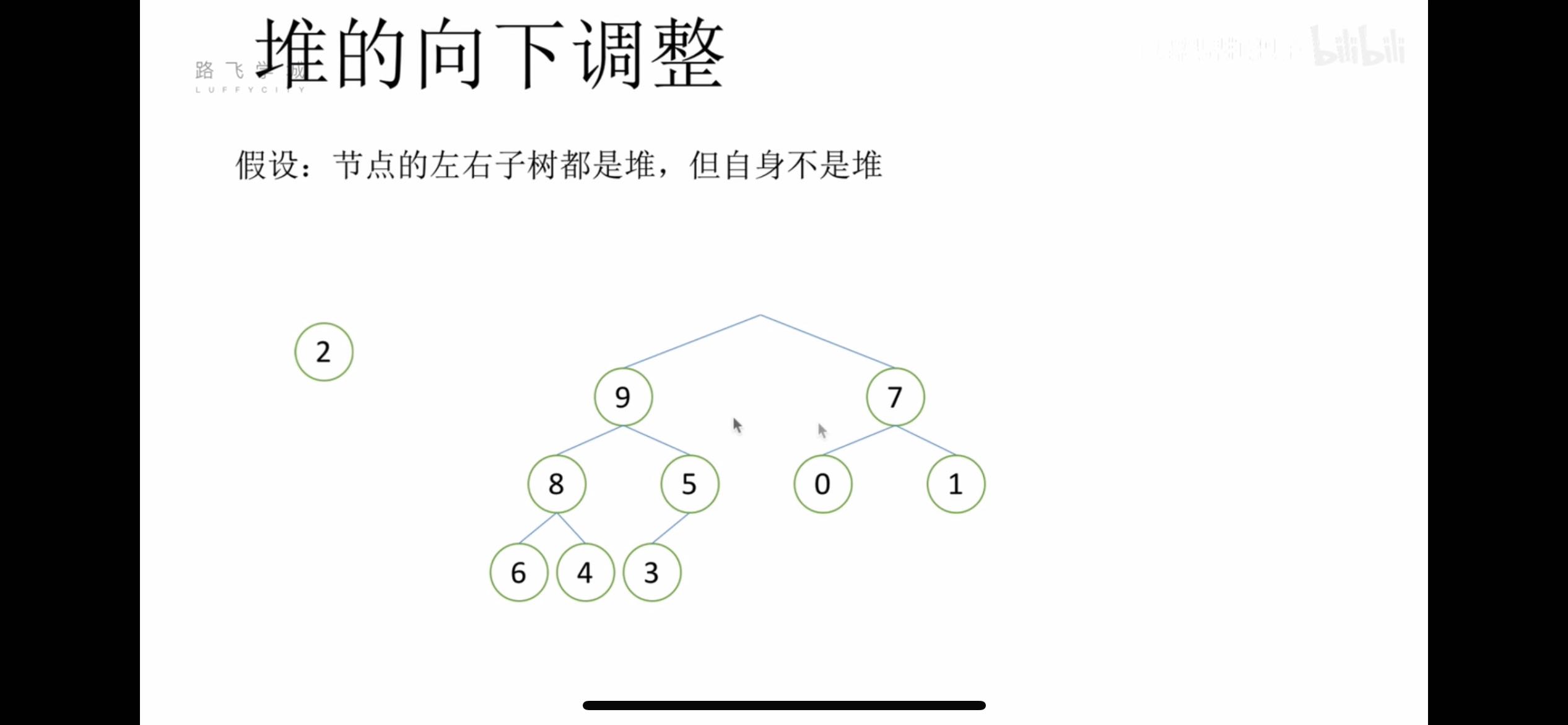
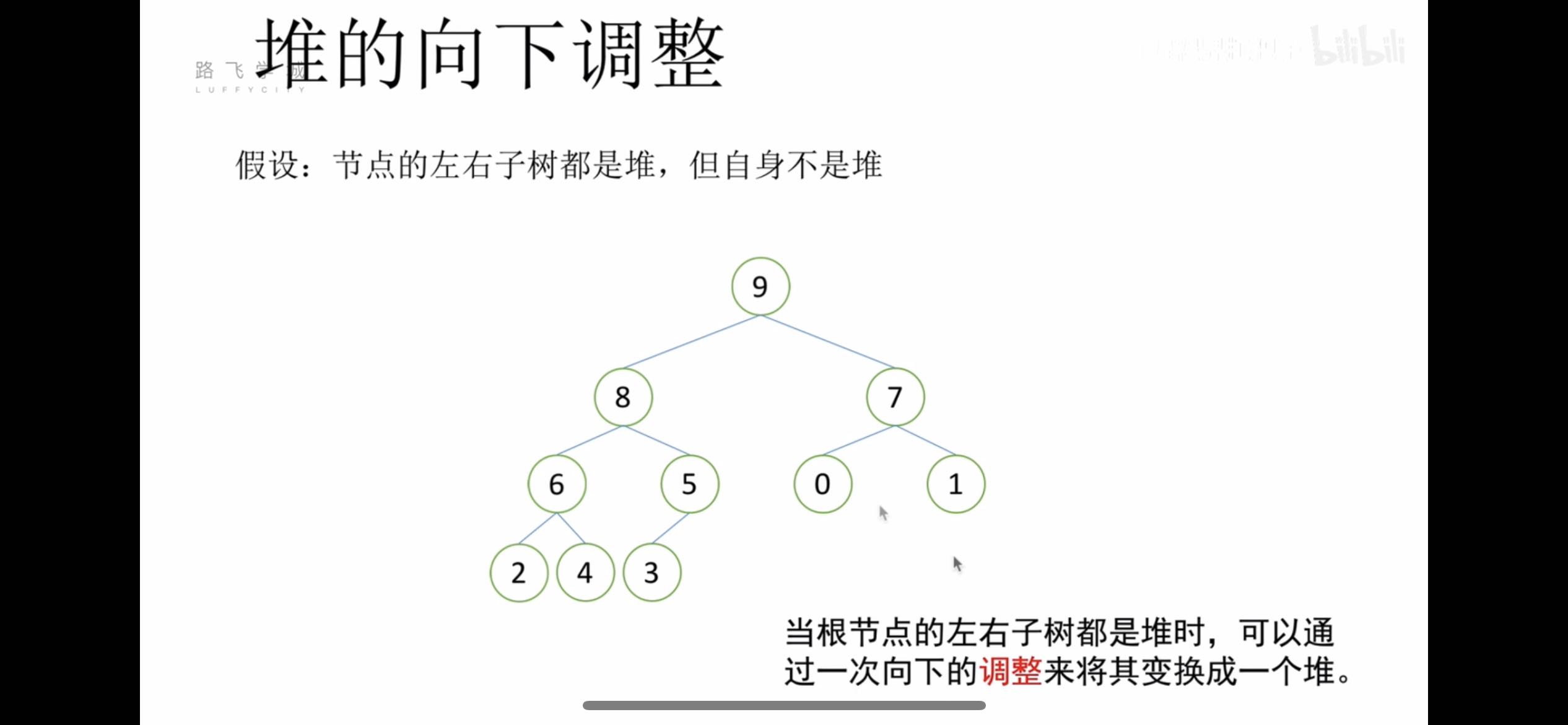
假设根节点的左右子树都是堆，但根节点不满足堆的性质
可以通过一次向下的调整来将其变成一个堆

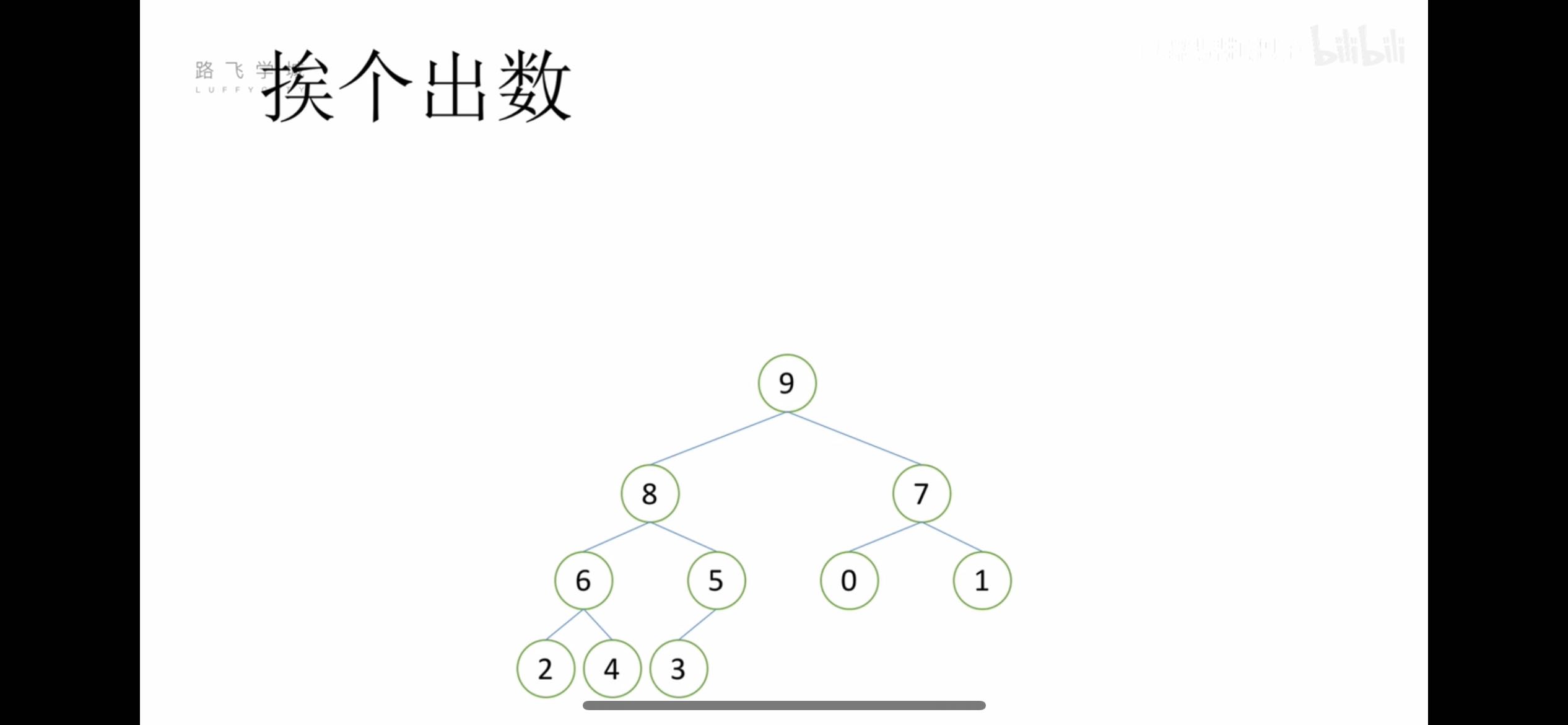
向下调整代码：

def sift(li,low,high): 
	'''
	:param li:列表
	:param low:堆的根节点位置
	:param high:堆的最后一个元素的位置
	:return:
	'''
	i=low 		#最开始指向根节点
	j=2*i+1 	#j开始是左孩子
	tmp=li[low]	#把堆顶存起来
	while j<=high: 	#只要j位置有数
		if j+1<=high and li[j+1]>li[j]: # 如果右孩子存在且比较大
			j=j+1	#j指向右孩子
		if li[j]>tmp:
			li[i]=li[j]
			i=j		#往下看一层
			j=2*i+1
		else: #tmp更大，把tmp放到i的位置上
			li[i]=tmp  #把tmp放到某一级领导位置上
			break
	else:
		li[i]=tmp  #把tmp放到叶子节点上

排序代码：

def heap_sort(li):
	n=len(li)
	for i in range((n-2)//2,-1,-1):
		#表示建堆的时候调整的部分的根的下标
		sift(li,i,n-1)
	for i in range(n-1,-1,-1):
		#i 指向当前堆的最后一个元素
		li[0],li[i]=li[i],li[0]
		sift(li,0,i-1) #i-1是最新的high
	
li=[i for i in range(100)]
import random 
random.shuffle(li)
print(li)
heap_sort(li)
print(li)

堆排序————内置模块

python内置模块——heapq
常用函数：
heapify(x)
heappush(heap,item)
heappop(heap)

代码：

import heapq
import random
 
li=list(range(100))
random.shuffle(li)
print(li)
heapq.heapify(li)建堆
n=len(li)
for i in range(n):
	print(heapq.heappop(li),end=',')

堆排序——topk问题

现在有n个数，设计算法得到前k大的数。(k<n)
解决思路：
	排序后切片     o(nlogn)
	排序LowB三人组 o(mn)
	堆排序思路	   o(mlogn)
 
解决思路：
	取列表前k个元素建一个小根堆。堆顶就是目前第k大的数
	依次向后遍历列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整；
	遍历列表所有元素后，倒序弹出堆顶

代码：

def topk(li,k):
	heap=li[0:k]
	for i in range((k-2)//2,-1,-1):
		sift(heap,i,k-1)
	#1、建堆
	for i in range(k,len(li)-1):
		if li[i]>heap[0]:
			heap[0]=li[i]
			sift(heap,0,k-1)
		
	#2、遍历
	for i in range(k-1,-1,-1):
		heap[0],heap[i]=heap[i],heap[0]
		sift(heap,0,i-1)
		
	#3、出数
	return heap
import random
li=list(range(1000))
random.shuffle(li)
print(topk(li,10))