三维重建——对极几何与基础矩阵
1、对极几何
基本概率:对极几何是Structure from Motion问题中,在两个相机位置产生的两幅图像的之间存在的一种特殊几何关系,是sfm问题中2D-2D求解两帧间相机姿态的基本模型。
基本模型:

其中c0、c1为两个相机中心,p为空间中一点,p在c0、c1对应像平面上的投影分别为x0、x1。c0、c1连线与像平面的交点e0、e1称为极点,l0、l1称为极线,c0、c1、p三点组成的平面称为极平面。
2、基础矩阵
两幅图像之间的约束关系使用代数的方式表示出来即为基本矩阵。基础矩阵是对极几何的代数表达方式。基础矩阵体现两张视图的对极几何的内在摄影几何的关系,基础矩阵只依赖于摄像机的内参K和外参R,t。当使用两个相机在不同位置对同一场景进行拍摄时,为了描述两幅图像之间的关系,引入对极几何。对极几何是两幅图像之间,两幅图像上的匹配点与以基线(连接两摄像机中心的直线)为轴的平面束的交的几何。
通过对极几何一副图像上的点可以确定另外一幅图像上的一条直线,这种情况用基础矩阵来表示。通过一种映射,一幅图像上的点可以确定另外一副图像上的一个点,这种情况用单应矩阵。
本质矩阵是基础矩阵的一种特殊情况,是在归一化图像坐标下的基础矩阵。
3、求解基础矩阵
3.1 估计算法
求解图像之间的基础矩阵的估计算法可以分为3类:线性、迭代、鲁棒性方法。八点算法计算基础矩阵是线性估计的典型代表,主要思想是利用8个匹配点对求解线性方程组,以得到基础矩阵。8点算法主要由以下两个步骤组成:
- 求线性解
- 奇异性约束
另外,也可用七点和十点(匹配点)算法计算基础矩阵。
3.2 求解流程图
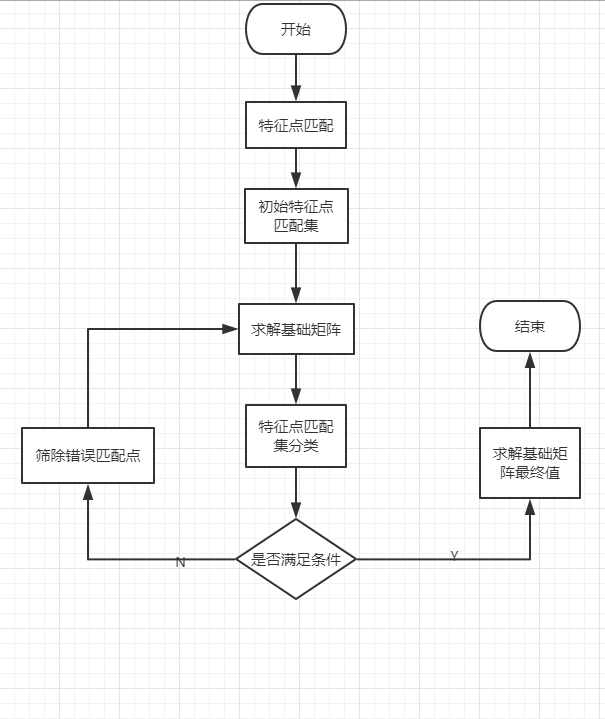
4、实验分析
4.1 七点算法计算基础矩阵
(1)像平面接近平行,极点位于无穷远

RANSAN算法消除错误匹配的的点:


得到的基础矩阵F:

4.2 八点算法计算基础矩阵
(1)像平面接近平行,极点位于无穷远

RANSAN算法消除错误匹配的的点:


得到的基础矩阵F:
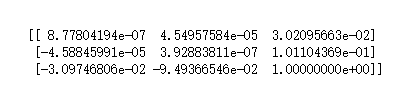
4.3 十点算法计算基础矩阵
(1)像平面接近平行,极点位于无穷远

RANSAN算法消除错误匹配的的点:


得到的基础矩阵F:
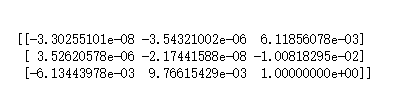
5、实验总结
- 为了提高解的稳定性和精度,往往会对输入点集的坐标先进行归一化处理。
- RANSAN算法可以用来消除错误匹配的的点,找到基础矩阵F,算法思想如下:
(1)随机选择7、8、10个点;
(2)用这7、8、10个点估计基础矩阵F;
(3)用这个F进行验算,计算用F验算成功的点对数n;
重复多次,找到使n最大的F作为基础矩阵。
6、代码展示
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
import PCV.geometry.camera as camera
import PCV.geometry.homography as homography
import PCV.geometry.sfm as sfm
import PCV.localdescriptors.sift as sift
im1 = array(Image.open('D:/计算机视觉/images/1.jpg'))
sift.process_image('D:/计算机视觉/images/1.jpg', 'im1.sift')
im2 = array(Image.open('D:/计算机视觉/images/2.jpg'))
sift.process_image('D:/计算机视觉/images/2.jpg', 'im2.sift')
l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')
matches = sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)
d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()
figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-3):
""" Robust estimation of a fundamental matrix F from point
correspondences using RANSAC (ransac.py from
http://www.scipy.org/Cookbook/RANSAC).
input: x1, x2 (3*n arrays) points in hom. coordinates. """
import PCV.tools.ransac as ransac
data = np.vstack((x1, x2))
d = 10 # 20 is the original
F, ransac_data = ransac.ransac(data.T, model,
8, maxiter, match_threshold, d, return_all=True)
return F, ransac_data['inliers']
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-3)
print (F)
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))
imshow(imj)
cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
if (0<= x1p[0][i]<cols1) and (0<= x2p[0][i]<cols1) and (0<=x1p[1][i]<rows1) and (0<=x2p[1][i]<rows1):
plot([x1p[0][i], x2p[0][i]+cols1],[x1p[1][i], x2p[1][i]],'c')
axis('off')
show()
d1p = d1n[inliers]
d2p = d2n[inliers]
print (P1)
print (P2)



