特征匹配-Harris角点检测

一、harris算法简介

1.角点概述

角点是图像很重要的特征,对图像图形的理解和分析有很重要的作用。角点在保留图像图形重要特征的同时,可以有效地减少信息的数据量,使其信息的含量很高,有效地提高了计算的速度,有利于图像的可靠匹配,使得实时处理成为可能。从图像分析的角度来定义角点可以有以下两种定义：角点可以是两个边缘的角点；角点是邻域内具有两个主方向的特征点；

前者往往需要对图像边缘进行编码，这在很大程度上依赖于图像的分割与边缘提取，具有相当大的难度和计算量，且一旦待检测目标局部发生变化，很可能导致操作的失败。基于图像灰度的方法通过计算点的曲率及梯度来检测角点，

避免了第一类方法存在的缺陷，此类方法主要有Moravec算子、Forstner算子、Harris算子、SUSAN算子等。本文主要介绍的Harris角点检测的算法原理。

2.Harris角点检测基本原理

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段。如下图：

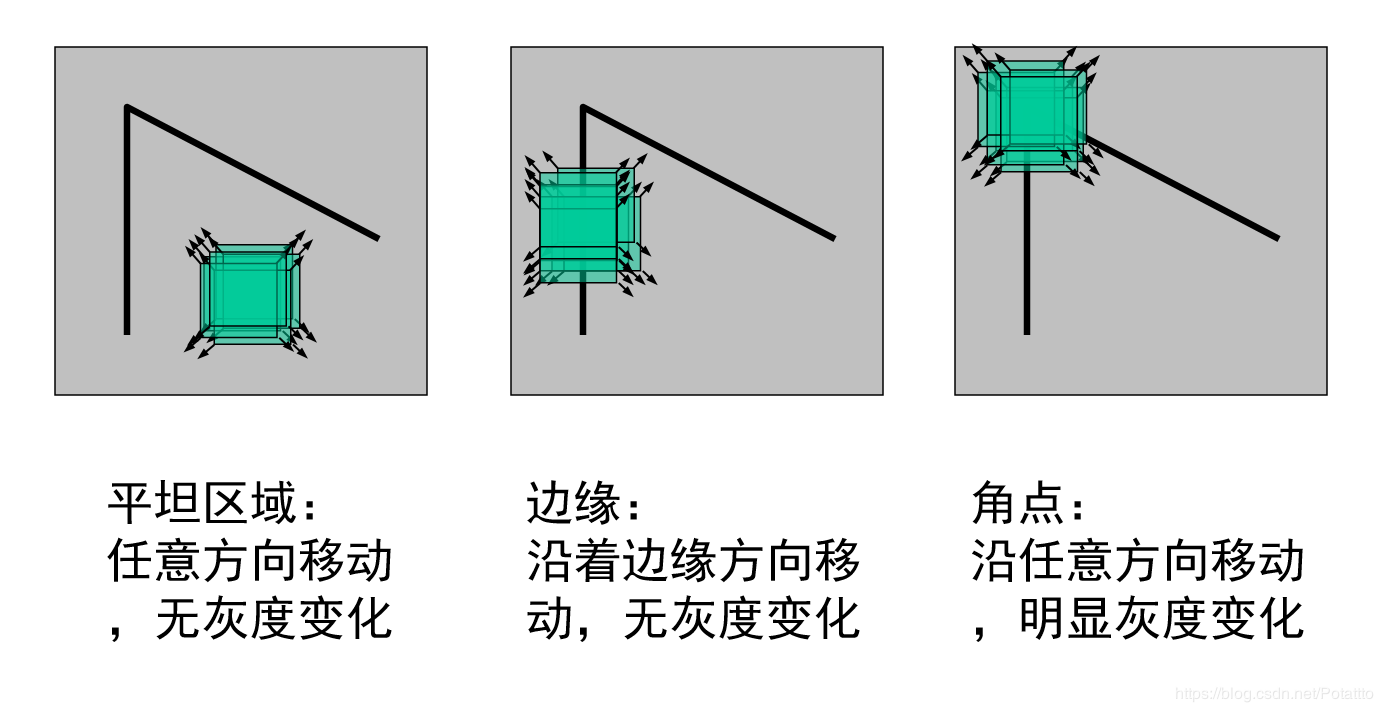
3、特征匹配流程

3.1、 根据准则，提取图像中的特征点 

3.2、提取特征点周围的图像块，构造特征描述符 

3.3、通过特征描述符对比，实现特征匹配

 

 二、Harris角点检测

      声明：为了更好地对 Harris角点检测算法进行分析，本次实验一共收集了纹理平坦、垂直边缘多、垂直边缘多的三个不同的场景，每个场景各收集了五幅的图片。然后通过每个场景中正面、侧面、旋转、远近、光照五个不同的方面进行对比试验。

2.1、纹理平坦的场景（以书本为例）

 2.1.1、正面图及检测结果

   

 

2.1.2、 侧面图及检测结果

  

 

2.1.3、旋转图及检测结果

  

 

2.1.4 、远距离图及检测结果

   

 

2.1.5 、光照图及检测结果

   

实验结果分析与总结:

   Harris角点检测算子具有旋转不变性。在对同一物体不同角度图片进行检测时，Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值也不发生变化，由此说明Harris角点检测算子具有旋转不变性。改变角度及旋转拍摄对其影响不大，ksize较大时，检测效果较差!

 

2.2垂直边缘多的场景（以建筑物为例）

2.2.1、正面图及检测结果

  、

 

2.2.2、 侧面图及检测结果

   

 

2.2.3、旋转图及检测结果

   

 

2.2.4 、远距离图及检测结果

   

 

2.2.5 、光照图及检测结果

   

实验结果分析与总结：

   通过在以上场景中从正面、侧面、旋转、远近、光照五个不同的方面进行试验得到的结果中可以看出，Harris角点检测能较好地检测出多个水平及垂直，改变角度及旋转拍摄对其影响不大，ksize较大时，检测效果较差，其结果还受图片明暗程度的影响。但是由于拍摄不够正规，结果不是特别明显！

 

2.3、纹理角点丰富的场景

2.2.1、正面图及检测结果

   

 

2.2.2、 侧面图及检测结果

   

 

2.2.3、旋转图及检测结果

  

 

2.2.4 、远距离图及检测结果

  

 

2.2.5 、光照图及检测结果

  

实验结果分析与总结：

从以上结果图对比可得，在纹理角点丰富的场景下，特征点提取过多，Harris角点检测效果较差。对图片的明暗程度比较敏感！

 

三、实验小结

3.1特征点必须具有不变性，包括几何不变性和关照不变性。几何不变性包括旋转和远近等，关照不变性包括关照等。另外，特征点提取过多时，Harris角点检测效果较差。

3.2能检测出图像中“真实的”角点、能准确的定位性能和具有不很高的稳定性的角点等是好的角点检测算法

3.3Harris角点检测的优点是稳定性高，尤其对L型角点（也就是直角）检测精度高。其缺点是对图片大小及图片的明暗程度敏感。

 

四、代码展示

# -*- coding: utf-8 -*-
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris

"""
Example of detecting Harris corner points (Figure 2-1 in the book).
"""

# 读入图像
im = array(Image.open(r'C:\Users\twz\Desktop\1.jpg').convert('L'))

# 检测harris角点
harrisim = harris.compute_harris_response(im)

# Harris响应函数
harrisim1 = 255 - harrisim

figure()
gray()

#画出Harris响应图
subplot(141)
imshow(harrisim1)
print(harrisim1.shape)
axis('off')
axis('equal')

threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
    filtered_coords = harris.get_harris_points(harrisim, 6, thres)
    subplot(1, 4, i+2)
    imshow(im)
    print(im.shape)
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
    axis('off')

#原书采用的PCV中PCV harris模块
#harris.plot_harris_points(im, filtered_coords)
# plot only 200 strongest
# harris.plot_harris_points(im, filtered_coords[:200])

show()