k-means和iosdata聚类算法在生活案例中的运用
引言：聚类是将数据分成类或者簇的过程，从而使同簇的对象之间具有很高的相似度，而不同的簇的对象相似度则存在差异。聚类技术是一种迭代重定位技术，在我们的生活中也得到了广泛的运用，比如：零件分组、数据评价、数据分析等很多方面；具体的比如对市场分析人员而言，聚类可以帮助市场分析人员从消费者数据库中分出不同的消费群体来，并且可以分析出每一类消费者的消费习惯等，从而帮助市场人员对销售做出更好的决策。
所以，本篇博客主要是对生活中的案例，运用k-means算法和isodata聚类算法进行数据评价和分析。本文是对“中国男足近几年在亚洲处于几流水平？”的问题进行分析。
首先，先让我们了解什么是k-means和iosdata聚类算法：
一、k-means算法
K-means算法是典型的基于距离的聚类算法，即对各个样本集采用距离作为相似性的评价指标，若两个样本集的距离越近，其相似度就越大。按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，且让簇间的距离尽量的大。最后把得到紧凑且独立的簇作为最终的目标。
实现过程如下：
（1）随机选取K个初始质心
（2）分别计算所有样本到这K个质心的距离
（3）如果样本离某质心Ki最近，那么这个样本属于Ki点群；如果到多个质心的距离相等，则可划分到任意组中
（4）按距离对所有样本分完组之后，计算每个组的均值（最简单的方法就是求样本每个维度的平均值），作为新的质心
（5）重复（2）（3）（4）直到新的质心和原质心相等，算法结束
二、iosdata聚类算法
算法思想：输入N个样本，预选Nc个初始聚类中心{z1,z2,…zNc}，它可以不等于所要求的聚类中心的数目，其初始位置可以从样本中任意选取。K为预期的聚类中心数目；θN为每一聚类域中最少的样本数目，若少于此数即不作为一个独立的聚类；θS为一个聚类域中样本距离分布的标准差；θc为两个聚类中心间的最小距离，若小于此数，两个聚类需进行合并；L为在一次迭代运算中可以合并的聚类中心的最多对数；I为迭代运算的次数。当某两类聚类中心距离θc小于阙值则归为一类，否则为不同类，某类样本数θN小于阙值，则将其删掉。
三、K-means算法和iosdata算法的不同：
1、iosdata算法每次把全部样本都调整完毕之后重新计算一次样本的均值；
2、iosdata算法会自动进行类的“合并”和“分裂”，从而得到聚类数较为合理的各个聚类。
四、动态聚类算法的3个要点：
1、 选定某种距离度量作为样本间的相似度量；
2、 确定某个评价聚类结果的准则函数；
3、 给定某个初始分类，然后用迭代算法找出是准则函数取极值的最好聚类结果。
五、案例分析
我要进行分析的数据是采集了亚洲16只球队在2006-2018年间大型的比赛战绩。数据进行了如下预处理：对于世界杯，进入决赛则取其最终排名，没有进入决赛的但打入预选赛十强赛赋予40，预选赛小组未出线的赋予50。对于亚洲杯，前四名取其排名，八强赋予5，十六强赋予9，预选赛没有出现的赋予17.数据如下
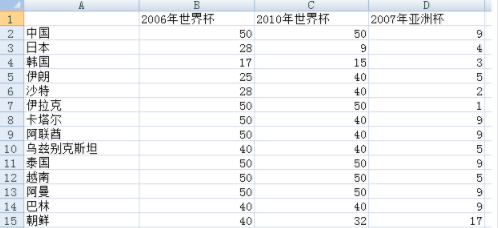
对数据进行[0,1]规格化：
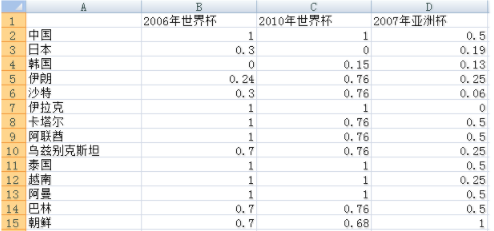
1.用k-means算法进行聚类。设k=3，即将这14支球队分成三个集团。
2.抽取日本、巴林和泰国的值作为三个簇的种子，即初始化三个簇的中心为A：{0.3, 0, 0.19}，B：{0.7, 0.76, 0.5}和C：{1, 1, 0.5}，即分别对应第2、13,和10条记录。
3.计算所有球队分别对三个中心点的相异度，以欧氏距离度量。
第一次聚类结果：
A：日本，韩国，伊朗，沙特；
B：乌兹别克斯坦，巴林，朝鲜；
C：中国，伊拉克，卡塔尔，阿联酋，泰国，越南，阿曼。
4.根据第一次聚类结果，调整各个簇的中心点。
A簇的新中心点为：{(0.3+0+0.24+0.3)/4=0.21, (0+0.15+0.76+0.76)/4=0.4175, (0.19+0.13+0.25+0.06)/4=0.1575} = {0.21, 0.4175, 0.1575}
用同样的方法计算得到B和C簇的新中心点分别为{0.7, 0.7333, 0.4167}，{1, 0.94, 0.40625}。
用调整后的中心点再次进行聚类，得到第二次迭代后的结果仍为：中国C，日本A，韩国A，伊朗A，沙特A，伊拉克C，卡塔尔C，阿联酋C，乌兹别克斯坦B，泰国C，越南C，阿曼C，巴林B，朝鲜B。
结果无变化，说明结果已收敛。于是，最终聚类结果为：
亚洲一流：日本，韩国，伊朗，沙特
亚洲二流：乌兹别克斯坦，巴林，朝鲜
亚洲三流：中国，伊拉克，卡塔尔，阿联酋，泰国，越南，阿曼
六、代码实现
>> a=[1,1,0.5;0.3,0,0.19;0,0.15,0.13;0.24,0.76,0.25;0.3,0.76,0.06;1,1,0;1,0.76,0.5;1,0.76,0.5;0.7,0.76,0.25;1,1,0.5;1,1,0.25;1,1,0.5;0.7,0.76,0.5;0.7,0.68,1;1,1,0.5] a = 1.0000 1.0000 0.5000 0.3000 0 0.1900 0 0.1500 0.1300 0.2400 0.7600 0.2500 0.3000 0.7600 0.0600 1.0000 1.0000 0 1.0000 0.7600 0.5000 1.0000 0.7600 0.5000 0.7000 0.7600 0.2500 1.0000 1.0000 0.5000 1.0000 1.0000 0.2500 1.0000 1.0000 0.5000 0.7000 0.7600 0.5000 0.7000 0.6800 1.0000 1.0000 1.0000 0.5000 >> ind=[2,13,10] ind = 2 13 10 >> b=a(ind(:),:) b = 0.3000 0 0.1900 0.7000 0.7600 0.5000 1.0000 1.0000 0.5000 result = 1.2594 0.3842 0 0 0.9131 1.2594 0.3407 0.9995 1.3636 0.7647 0.5235 0.8353 0.7710 0.5946 0.8609 1.2354 0.6306 0.5000 1.0787 0.3000 0.2400 1.0787 0.3000 0.2400 0.8609 0.2500 0.4584 1.2594 0.3842 0 1.2221 0.4584 0.2500 1.2594 0.3842 0 0.9131 0 0.3842 1.1307 0.5064 0.6651 1.2594 0.3842 0
